Electric-Magnetic Duality in Gravity and Higher-Spin Fields

1. Introduction

Electric-magnetic duality basically evolved from the invariance of Maxwell's equations [1], which led to the hypothesis about magnetic monopoles in electromagnetism [2], and the introduction of magnetic-type sources to gauge theories [3–7]. Electric-magnetic duality contributed to the development of Yang-Mills theories [8–11], p-form gauge fields [12–14], supergravity theories [15, 16], and string theories [17–19]. Generalizations of this duality emerged as weak-strong (Montonen-Olive) duality in Yang-Mills theories [7]. The duality principle was refined in supersymmetry [20] and was extended to ${N}=4$ supersymmetric gauge theories [21]. The ${N}=4$ Super Yang-Mills theory has an exact SL(2, ℤ) symmetry, typically referred to as S-duality, that includes a transformation known as weak-strong duality [22], and can be understood as electric-magnetic duality in certain circumstances such as the Coulomb branch. Strong-weak duality exchanges the electrically charged string with the magnetically charged soliton in the heterotic string theory [23–25]. Electric-magnetic duality was shown in ${N}=1$ supersymmetric gauge theories [26]. Compatifications of type II string theory (or M-theory) on a torus have an E₇ symmetry, referred to as U-duality, which includes the T-duality O(6, 6, ℤ) and the S-duality SL(2, ℤ) [27]. S-duality of the ${N}=4$ Super Yang-Mills theory and S- and U-dualities of type II string and M-theory correspond to exact symmetries of the full consistent quantum theory [27, 28]. U-duality (see e.g., [29–31]) provides nonperturbative insights in M-theory [32], and also in string theories [33, 34]. The electric-magnetic duality principle also permeated into gravitational theories [35–43], supergravity [44–46], higher-spin field theories [38, 47–49], holographic dictionary [50–52], hypergravity [53], and partially-massless and massive gravity on (Anti-) de Sitter space [54–56].

Gravitational electric-magnetic duality originally appeared in wave solutions of general relativity [57–59]. The Bianchi identities for the Weyl curvature provide some dynamical equations for perturbations in cosmological models [60–66], which are analogous with Maxwell's equations [67, 68]. In general relativity, the Riemann curvature is decomposed into the Ricci curvature and the Weyl curvature. The Ricci curvature defined by the Einstein equations corresponds to the local dynamics of spacetime, while the nonlocal characteristics of gravitation, such as Newtonian force and gravitational waves, are encoded in the Weyl curvature [66–70]. Based on this analogy, the electric and magnetic parts of the Weyl curvature tensor have been called gravitoelectric and gravitomagnetic fields [64, 68, 71–74], though their spatial, symmetric 2-rank tensor fields make them dissimilar to the electric and magnetic vector fields of the U(1) gauge theory for spin-1 fields.

Analogies between gravitation and electromagnetism led to propose gravitationally magnetic-type (also called gravitomagnetic) mass almost a half-century ago [75–78]. The solutions of the geodesic equations for the Taub–NUT [79, 80] metric also pointed to the magnetic-type mass, whose characteristic could be identical with the angular momentum [81]. Moreover, the gravitational lensing by bodies with gravitomagnetic masses, as well as the predicted spectra of magnetic-type atoms have been explained in Taub–NUT space [82]. The effects of the gravitomagnetic mass on the motion of test particles and the propagation of electromagnetic waves have been studied in Kerr-Newman-Taub-NUT spacetime [83]. Furthermore, the gravitational field equations and dual curvature tensors, which characterize the dynamics of gravitomagnetic matter (dual matter), as well as the relationship between the dynamical theories of gravitomagnetic mass (dual mass) and gravitoelectric mass (ordinary mass) have been elaborated among the NUT solutions, the spin-connection and vierbein [84, 85]. Finally, energy-momentum and angular momentum of both electric- and magnetic-type masses have been formulated for spin-2 fields [86].

The linearized formulations of gravity describe the graviton using a 2-rank symmetric tensor h_μν, which can be dualized to a gauge field ${\tilde{h}}_{{\mu }_1···{\mu }_{D-3}\nu }$ with mixed symmetry (D − 3, 1), the so-called dual graviton. The dual gravity with mixed symmetry tensors first appeared in 1980 [35], and mixed symmetry (2, 1) tensors were shown to be gauge fields [35]. It was also argued that a free massive mixed symmetry (2, 1) field in D = 4 could be dual to a free massive spin-2 field (massive graviton) and a massive spin-0 field (Higgs boson) that may illuminate “magnetic-like” aspects of gravity [87]. Following these earlier works [35, 87], mixed symmetry (D − 3, 1) was first suggested as a candidate for the dual graviton in D dimensions in 2000 [37]. Using the “parent” first-order action at the linearized level, it was then demonstrated that the formulations of the dual graviton with mixed symmetry (D − 3, 1) and the graviton are equivalent and have the same bosonic degrees of freedom [44]. Considering the Riemann curvature and its dual curvature, the linearized Einstein equations and Bianchi identities were found to hold on dual gravity with mixed symmetry (D − 3, 1) [38]. From the “parent” first-order action introduced in [44], the familiar “standard” second-order formulation of the dual graviton with mixed symmetry (D − 3, 1) in D dimensions was then obtained in [47], which was found to be the Curtright action [35] in D = 5 [through this paper, we consider the “standard” second-order formulations of dual gravity and spin-s fields, while the “parent” first-order actions are briefly presented in Appendix 1 (Supplementary Material)]. The dual formulation of linearized gravity have been further investigated by several authors [40, 41, 43, 46, 88–90]. In the linearized theory, the magnetically charged D − 4 branes arise from Kaluza-Klein monopole, which are indeed gravitationally magnetic-type sources (0-brane in D = 4), can naturally be coupled with the gauge field of the dual graviton ([37]; see also [38, 91]). In fact, the dual graviton in D = 4 becomes the Pauli-Fierz field based on a symmetric tensor ${\tilde{h}}_{\mu \nu }$, while in D = 5 we get the Curtright [35] field ${\tilde{h}}_{\mu \nu \rho }$ with Young symmetry (2, 1) [40]. Generally, the spin-2 field described by a rank-2 symmetric tensor h_μν is dualized to the linearized dual gravitational field ${\tilde{h}}_{{\mu }_1···{\mu }_{D-3}\nu }$ described by a (D − 2)-rank tensor with Young symmetry type (D − 3, 1) [37, 38, 43]. It was also demonstrated that spin-2 fields can be dualized to two different theories:¹ dual graviton with (D − 3, 1) and double-dual graviton with (D − 3, D − 3) [38, 96]. It was understood that mixed symmetry (D − 3, 1) fields can possess a Lorentz-invariance action principle. Although the equations of motion for mixed symmetry (D − 3, D − 3) fields could maintain the Lorentz group SO(D − 1, 1) [38], some authors argued that they may not have a Lorentz-invariance action in D > 4 [40]. Moreover, the graviton, the dual graviton and the double-dual graviton in 4 dimensions can be interchanged by a kind of the S-duality of D = 4 Maxwell theory [88]. In the context of the Macdowell-Mansouri formalism, the strong-weak duality for linearized gravity also corresponds to small-large duality for the cosmological constant [36] (see also [97] for duality with a cosmological constant). The dual formulations of spin-2 fields in D dimensions have also been generalized to spin-s fields whose dual fields are formulated using Young symmetry type $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$ [38, 47, 49, 89, 96, 98].

Dirac's relativistic wave solutions [99] for massive particles were the first theory extended to higher spins in 1939 [100], which provided the foundation for the Lagrangian formulations of massive, bosonic fields with arbitrary spin [101]. The free and interacting theories of massless, bosonic gauge fields with spins higher than 2 (the so-called Fronsdal [102] field) have been investigated later [102–106]. In particular, dual representations of spin-s fields (s ≥ 2) were formulated using exotic higher-rank gauge fields of the Lorentz group SO(D − 1, 1) in the linearized theory [38, 48]. It was found that dual formations of spin-s fields can be described by a tensor with mixed Young symmetry type with one column with D − 3 boxes and s−1 columns with one box [47], which turns out to be the Pauli-Fierz field (s = 2), the Fronsdal field (s ≥ 3) in D = 4, and the Curtright field (s = 2) in D = 5. Nonlinear theories of massless, totally symmetric spin-s fields were also discussed in the (Anti-) de Sitter space, (A)dS [107]. It was shown that nonlinear representations of dual spin-s gauge theories can partially be implemented with a Killing vector [38]. The conserved electric- and magnetic-type sources associated with spin-s fields and their corresponding dual fields were also derived, in analogy with electromagnetism [91]. Recently, the twisted self-duality conditions, which were previously discussed in dual formulations of linearized gravity [43, 108], were also illustrated in higher spin gauge fields, which maintain an SO(2) electric-magnetic invariance in D = 4 [49].

In what follows we evaluate general aspects of electric-magnetic duality in gravity and higher spin field theories (s ≥ 2) in arbitrary dimensions (D ≥ 4), and advocate their formulations in linearized theories, their couplings with electric- and magnetic-type sources, and their harmonic conditions for wave propagation. In section 2, we study dual formulations of the spin-2 field (dual graviton). We then extend them to the spin-3 field (section 3) and higher spin fields (section 4). Section 5 discusses the interacting theories of the dual graviton and spin-s fields.

1.1. Notations and Conventions

To describe tensors with mixed symmetry types, we employ Young tableaux where a box in the Young diagram is associated with each index of a tensor (see [41, 96, 109, 110] for full details). A vector field (e.g., A_μ) has Young symmetry type (1) described by a single-box tableau . A 2nd rank anti-symmetric tensor, e.g., the Maxwell field F_μν, has Young symmetry type (2), which is represented by two boxes arranged in a column, . A 2nd rank symmetric tensor, e.g., the graviton field h_μν, has Young symmetry type (1, 1), which is represented by two boxes arranged in a row, . Accordingly, the Curtright field, which describes the dual gravition ${\tilde{h}}_{\mu \nu \rho }$ in D = 5, is a 3rd rank tensor with Young symmetry type (2, 1), and is represented by the Young diagram . The Riemann tensor R_μνρλ and the Weyl tensor C_μνρλ are 4th rank tensors whose algebraic properties correspond to Young symmetry (2, 2), i.e., the diagram . We utilize the notations in which the Greek alphabet refers to covariant spacetime indices (e.g., A_μ, h_μν), and the Latin alphabet refers to light-cone gauge indices (e.g., A_i, h_ij), which is also used for the E₁₁ ⊗_s l₁ non-linear realization in section 2.3 (e.g., h_a^b, A_a1a2a3).

Throughout this paper, the graviton is denoted by a 2nd rank tensor h_μν, whereas the dual graviton is shown by a (D − 2)-rank tensor ${\tilde{h}}_{{\mu }_1···{\mu }_{D-3}\nu }$ with mixed symmetry (D − 3, 1) in D dimensions. A 3nd rank symmetric tensor, e.g., the typical spin-3 field h_μνρ, has mixed symmetry type (1, 1, 1), which is represented by three boxes arranged in a row, . The spin-s fields (s > 2) are denoted by a s-th rank symmetric tensor h_μ1···μs with mixed symmetry type $(\stackrel{s}{\overbrace{1,···,1}})$, which is represented by s boxes arranged in a row, while their dual field are represented by a (D − 2 + s)-th rank tensor ${\tilde{h}}_{{\mu }_1···{\mu }_{D-3}{\nu }_1···{\nu }_{s-1}}$ with mixed symmetry $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$ in D dimensions. The electric- and magnetic-type sources for spin-s fields in D = 4 are denoted by s-th rank energy-momentum tensors T_μ1···μs and ${\tilde{T}}_{{\mu }_1···{\mu }_s}$, respectively. The Riemann curvatures for spin-s fields are represented by 2s-rank tensors R_{μ1ν1···μsνs}. The dual Riemann curvatures for spin-s fields in D = 4 are denoted by ${\tilde{R}}_{{\mu }_1{\nu }_1···{\mu }_s{\nu }_s}$. We write formulations according to the convention $8\pi G_{\text{N}}^{(D)}=1=c$, unless the physical constants specified ($G_{\text{N}}^{(D)}$ is the gravitational constant in D dimensions and c is the speed of light). We utilize the round brackets enclosing indices for symmetrization, h_μν = h_νμ = h_(μν), and the square brackets for antisymmetrization, F_μν = −F_νμ = F_[μν].

2. Dual Graviton

Free gauge theories in D-dimensional flat space are typically described by a particular irreducible tensor representation of the little group SO(D − 2) [37]. In the view point of the little group SO(D − 2), free abelian gauge theories can be dualized to a number of mixed symmetry tensors (see e.g., [38, 96]). The dual formulations for the free theory F present symmetries in the equations of motion, which transform the field F into its Hodge dual fields ^⋆F (left dual), F^⋆ (right dual), and ^⋆F^⋆ (left-right dual) [96]. For symmetric tensors, we have ^⋆F = F^⋆.

The 1-form potential A_μ of the free Maxwell field strength F_μν ≡ 2∂_[μA_ν] in D dimensions possesses physical gauge degrees of freedom A_i in the little group SO(D − 2) representation, which can be dualized to a dual (D − 3)-form potential as follows [38]:

While A_μ is a single-box Young tableau, , its dual field is a single-box tableau in D = 4, a tableau with two boxes in a column in D = 5, and a tableau with D − 3 boxes in a column in arbitrary D dimensions.

For spin-2 fields such the graviton h_μν, there are two different dual linearized formulations in generic D-dimensional spacetime [38, 40] (and infinitely many off-shell dualities [92, 93]). In the first dual formulation, the physical gauge graviton h_ij in D dimensions is dualized to a dual field ${\tilde{h}}_{i_1···i_{D-3}j}$ in the little group SO(D − 2) representation as follows [38]:

which has the following properties:

The first dual graviton ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}\mu }$ is described by a tensor with Young symmetry type (D − 3, 1). In D = 4, the dual graviton is a symmetric 2nd rank tensor ${\tilde{h}}_{\mu \nu }$ with the Young tableau having two boxes in a raw, , while it is a mixed symmetry (2, 1) tensor in D = 5 with the Young diagram (the so-called Curtright field). The dual graviton $\tilde{h}$ possesses the equations of motion, which are equivalent to gravity and describe the same gravitational degrees of freedom of the graviton h [44]. The equivalence between the different formulations can be demonstrated by using their light-cone gauge fields.

In the second dual formulation, the physical light-cone gauge graviton h_ij in D dimensions is dualized to a dual field ĥ_{i1···iD − 3j1···jD − 3}as follows [38]:

having the following properties:

The second dual graviton ĥ_{α1···αD − 3β1···βD − 3} (also called double-dual graviton) is a tensor with Young symmetry type (D − 3, D − 3). In D = 4, it yields a symmetric 2nd rank tensor ĥ_μν with Young symmetry type (1, 1). In D = 5, it becomes a mixed symmetry (2, 2) tensor with the Young diagram whose algebraic properties are similar to the typical (spin-2) Riemann tensor R_μνρλ.

It can easily be seen that the physical light-cone dual field on both indices, ĥ_{i1···iD − 3j1···jD − 3}, can be written using the physical light-cone dual field on one index ${\tilde{h}}_{i_1···i_{D-3}j}$,

The first physical dual field $\tilde{h}$ is recovered from the physical second dual field ĥ, so the equations of motion written for the Hodge dual field ĥ are equivalent to the field $\tilde{h}$. However, it was argued that the second dual field ĥ in D > 4 may not have a Lorentz-invariant action [40] (though Lorentz covariant field equations were given in Hull [38]). We also note that for a traceless field (h_μ^μ = 0), there is no second dual formulation, as it cannot be dualized on both indices. Therefore, we only consider the first dual formulation of gravity (also its equivalences for spin-s fields) throughout this paper.

For the typical (spin-2) linearized Riemann curvature R_αβμν, one gets the following dual linearized Riemann curvature in D-dimensional spacetime for the first and second dual formulations, respectively [38]:

where the Riemann tensor R_αβμν is of Young symmetry type (2, 2) ≡ , the first dual Riemann tensor ${\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}\mu \nu }$ has Young symmetry type (D − 2, 2), and the second dual Riemann tensor ${\widehat{R}}_{{\alpha }_1···{\alpha }_{D-2}{\beta }_1···{\beta }_{D-2}}$ has mixed symmetry type (D − 2, D − 2).

2.1. D = 4: The Pauli-Fierz Field

The Pauli-Fierz action [100, 111], describing the equations of motion of a free massless spin-2 field h_μν in D-dimensional Minkowski spacetime ${\eta }_{\mu \nu }=\text{diag}(-,\stackrel{D-1}{\overbrace{+,···,+}})$ reads explicitly

where the Lagrangian ${{L}}_{\text{PF}}$ is quadratic in the first derivatives of the spin-2 field h_μν and its covariant trace (h ≡ h_α^α):

and is invariant under the gauge transformation

where ξ_μ is an arbitrary vector field. The above gauge transformation is irreducible.

The action (13) has the following equations of motion:

The symmetric tensor h_μν is associated with a free massless spin-2 particle (graviton), and its linearized Riemann curvature R_μναβ is defined as (e.g., [41, 43, 108]),

with the following properties

and fulfills the Bianchi identity ∂_[ρR_μν]αβ = 0 and the linearized Einstein equations R_μν = 0, where $R_{\mu \nu }\equiv R_{\mu \alpha \nu \beta }{\eta }^{\alpha \beta }$ is the linearized Ricci tensor. We can also define the scalar curvature as R ≡ R_μ^μ.

From the definition (16) and the equations of motion (15), it follows the Euler-Lagrange variation:

where G_μν is the linearized Einstein tensor, and fulfills the contracted Bianchi identity.

The linearized Riemann curvature tensor R_μναβ of the Pauli-Fierz field h_μν in D dimensions can be split into the Weyl curvature tensor and the expression formulated by the linearized Ricci tensor and scalar curvature:

where the Weyl tensor C_μναβ is traceless, and has mixed symmetry type (2, 2) ≡ , so

The Weyl tensor has D(D + 1)(D + 2)(D − 3)/12 independent components (0, 10, and 35 components for D = 3, 4, and 5, respectively).

The Weyl curvature tensor contains electric and magnetic components, the so-called gravitoelectric and gravitomagnetic fields [64, 66, 68], which are encoded by covariant and time derivatives of the Pauli-Fierz field h_μν (see Equations 27, 28), and defined as follows:

where ${\tilde{C}}_{\mu \nu \alpha \beta }=\frac{1}{2}{ϵ}_{\mu \nu \rho \lambda }{C}^{\rho \lambda }{}_{\alpha \beta }$ is a Hodge dual of the Weyl tensor, so $B_{\mu \nu }=-\frac{1}{2}{ϵ}_{\mu \alpha \rho \lambda }{C}^{\rho \lambda }{}_{\nu \beta }{u}^{\alpha }{u}^{\beta }=-\frac{1}{2}{ϵ}_{\mu \rho \lambda }{C}^{\rho \lambda }{}_{\nu 0}$ (the sign convention similar to Maxwell theory ²). Here, ϵ_μρλ is taken to be the spatial permutation tensor (${{ϵ}_{\mu \nu \rho }u}^{\rho }=0$) with ϵ_μναβ = 2u_[μϵ_ν]αβ − 2ϵ_μν[αu_β], so ${ϵ}_{\mu \nu \alpha }={ϵ}_{\mu \nu \alpha \beta }{u}^{\beta }$ and ${ϵ}_{\mu \nu \beta }=-{ϵ}_{\mu \nu \alpha \beta }{u}^{\alpha }$ (taking $u^{\mu }{u}_{\mu }=-1$ and $u^{\mu }{\eta }_{\mu }{}^{\nu }=u^{\nu }$ in Minkowski spacetime).

The electric and magnetic parts of the Weyl tensor are both symmetric and traceless:

In D = 4, the Weyl tensor has ten independent components, and its electric and magnetic parts have five independent components each.

From (16), one obtains

so the linearized Weyl tensor can be written in terms of the Pauli-Fierz field h_μν:

Accordingly, the electric and magnetic parts of the linearized Weyl tensor can be formulated using twice covariant and/or time derivatives of the Pauli-Fierz field h_μν in the instantaneous rest-space of an observer moving with the relativistic velocity u^μ in Minkowski spacetime η_μν,

where primes denote time derivatives, i.e., ${(T_{\mu ···})}^{\prime }=u^{\alpha }{\partial }_{\alpha }{T}_{\mu ···}$, and ϵ_μρλ is the spatial permutation tensor (${{ϵ}_{\mu \nu \rho }u}^{\rho }=0$). It is seen that the above equations are symmetric, traceless (E_μ^μ = 0 = B_μ^μ) and spatial ($E_{\mu \nu }{u}^{\nu }=0=B_{\mu \nu }{u}^{\nu }$). While the gravitoelectric field E_μν is associated with time/covariant derivatives of time/covariant derivatives of the Pauli-Fierz field h_μν, the gravitomagnetic field B_μν is introduced by covariant curls and rotations of time/covariant derivatives of the Pauli-Fierz field h_μν (the covariant curl is defined as $\mathfrak{c}\mathfrak{u}\mathfrak{r}\mathfrak{l}{(h)}_{\mu \nu }\equiv {ϵ}_{\rho \lambda (\mu }{\partial }^{\rho }{h}_{\nu )}{}^{\lambda }={ϵ}_{\mu \rho \lambda }{\partial }^{[\rho }{h}_{\nu }{}^{\lambda ]}$).

The linearized Riemann curvature tensor R_μναβ can also be decomposed as

where S_μν is the linearized Schouten tensor that is defined in D dimensions as

whose curl is called the Cotton tensor:

which satisfies

Substituting Equation (30) into Equation (29), the Riemann decomposition Equation (19) is easily recovered.

The Pauli-Fierz theory of linearized gravity in D = 4 is dualized to the Pauli-Fierz action $S=\frac{1}{2}\int d^{4}x{{L}}_{\text{PF}}\left[{\tilde{h}}_{\mu \nu }\right]$ being formulated in terms of the symmetric massless 2nd-rank tensor ${\tilde{h}}_{\mu \nu }={\tilde{h}}_{\nu \mu }={\tilde{h}}_{(\mu \nu )}$ (dual graviton) and its covariant trace ($\tilde{h}\equiv {\tilde{h}}_{\alpha }{}^{\alpha }$)[40, 42, 43]. In such a way, the symmetric tensor h_μν is replaced with ${\tilde{h}}_{\mu \nu }$ in the Pauli-Fierz action (13). Similarly, we can define the dual Riemann curvature ${\tilde{R}}_{\mu \nu \alpha \beta }$ for the Pauli-Fierz field ${\tilde{h}}_{\mu \nu }$ as ${\tilde{R}}_{\mu \nu }{}^{\alpha \beta }=-2{\partial }^{[\alpha }{\partial }_{[\mu }{\tilde{h}}_{\nu ]}{}^{\beta ]}$, which is decomposed into the dual Ricci tensor ${\tilde{R}}_{\mu \nu }\equiv {\tilde{R}}_{\mu \alpha \nu \beta }{\eta }^{\alpha \beta }$ and the dual Weyl tensor ${\tilde{C}}_{\mu \nu \alpha \beta }$.

There is an SO(2) electric-magnetic invariance between the Riemann curvature and its dual curvature, which is called the “twisted self-duality conditions”[38, 41, 43, 49, 88]:

The gravitoelectric and gravitomagnetic fields of the Pauli-Fierz field h_μν and its dual field ${\tilde{h}}_{\mu \nu }$ also demonstrate the twisted self-duality conditions[43, 49]:

where Ẽ_μν and ${\tilde{B}}_{\mu \nu }$ are the electric and magnetic parts of the (dual) Weyl tensor ${\tilde{C}}_{\mu \nu \alpha \beta }$ associated with the dual Pauli-Fierz field ${\tilde{h}}_{\mu \nu }$ (dual graviton), and are both symmetric and traceless.

The twisted self-dual conditions (Equations 33, 34) can be expressed in a duality-symmetric way [49]:

with matrix notations

which imply that the equations of motion for the dual graviton ${\tilde{h}}_{\mu \nu }$ are fully equivalent to those for the graviton h_μν under SO(2) electric-magnetic duality rotations.

Using the first dual expression (Equation 10), the dual Riemann curvature ${\tilde{R}}_{\mu \nu \alpha \beta }$ in D = 4 is defined by

which enjoys the following properties

The equations of motion are invariant under the duality transformations [42]

where the Riemann curvature R_μναβ and its dual curvature ${\tilde{R}}_{\mu \nu \alpha \beta }$ are transferred into each other under the electric-magnetic duality rotations (Equations 41, 42).

It is useful to see the electric-magnetic duality rotations in terms of the electric and magnetic parts of the linearized Riemann curvature tensor (see e.g., [112]):

While the equations of motion are satisfied, the rotations in (41) and (42) are equivalent to

This SO(2) rotation in gravity is analogous to the duality transformations of Maxwell fields [113, 114] in which the free Maxwell field strength F_μν is transformed into its dual field strength ${\tilde{F}}_{\mu \nu }=\frac{1}{2}{ϵ}_{\mu \nu \alpha \beta }{F}^{\alpha \beta }$. Using the definitions (16), it can be shown that the graviton h_μν is rotated into the dual graviton ${\tilde{h}}_{\mu \nu }$ under the transformations (41) and (42), so they are invariant under the electric-magnetic duality.

2.2. D = 5: The Curtright Field

The equations of motion of a free massless spin-2 field ${\tilde{h}}_{\left[\mu \nu \right]\rho }\equiv {\tilde{h}}_{\mu \nu |\rho }$ (dual graviton) in 5-dimensional flat spacetime can be described using the following action [35, 41, 47, 105]

It is also convenient to use a Lagrangian consisting of the Curtright field strength tensor ${\bar{F}}_{\left[\mu \nu \lambda \right]\alpha }\equiv {\bar{F}}_{\mu \nu \lambda |\alpha }$, the so-called Curtright action [35, 40] ³

where the Curtright field strength tensor ${\bar{F}}_{\mu \nu \lambda \alpha }$ is a tensor with mixed symmetry type (3, 1) ≡ defined as

and ${\tilde{h}}_{\mu \nu \lambda }$ is the Curtright [35] field with mixed symmetry type (2, 1) ≡ ,

The Curtright action (47) is invariant under the following gauge transformation [35, 37, 38, 40, 115]

where σ_μν and α_μν are symmetric and antisymmetric arbitrary tensors, respectively:

The Curtright field ${\bar{F}}_{\mu \nu \lambda \alpha }$ is transformed as [43]:

although it is not gauge invariant. The gauge transformations for σ_μν and α_μν are reducible, so we get δ_σσ_μν = 6∂_(μσ_ν) and δ_σα_μν = 2∂_[μσ_ν], where σ_μ is an arbitrary vector field. The gauge symmetry for σ_μ is irreducible [40].

The Curtright field ${\tilde{h}}_{\mu \nu \lambda }$ is associated with the linearized dual Riemann curvature tensor [37, 40, 43]:

and the linearized dual Ricci curvature tensor and the dual vector curvature, respectively,

The linearized dual Riemann curvature tensor has the Young tableau symmetry (3, 2) ≡ , and the linearized dual Ricci curvature tensor has the Young tableau symmetry (2, 1) ≡ .

The linearized dual Riemann curvature satisfies the “Bianchi identity”[38, 88]

We can also define the linearized “dual Einstein tensor” for the Curtright field [37, 40, 43, 88] through

where ${\tilde{G}}_{\left[\mu \nu \right]\alpha }$ is the dual Einstein tensor with Young symmetry type (2, 1), and fulfills the “contracted Bianchi identities”

The doubly contracted Bianchi identity yields ${\partial }^{\mu }{\tilde{R}}_{\mu }=0$. The linearized dual Einstein equations are ${\tilde{G}}_{\left[\mu \nu \right]\alpha }=0$, which are equivalent to ${\tilde{R}}_{\mu \nu \alpha }=0$.

The action (47) is gauge-invariant, and provides the following equations of motion [40]:

which satisfy the contracted Bianchi identities (58).

The linearized dual Riemann curvature of the Curtright field ${\tilde{h}}_{\mu \nu \rho }$ is decomposed into a traceless part (dual 5-D “Weyl” tensor), and terms containing the (dual 5-D) Schouten tensor:

where the dual Schouten tensor ${\tilde{S}}_{\mu \nu \alpha }$ is defined as [43]:

The dual 5-D Weyl tensor ${\tilde{C}}_{\mu \nu \rho \alpha \beta }$ has 35 independent components.

One can also define the Cotton tensor, the curl of the Schouten tensor, as

which is traceless ${\tilde{C}}_{\mu \nu \alpha \beta }{\eta }^{\nu \beta }=0$, and contains both mixed symmetry types (2, 2) and (3, 1), and satisfies

It was shown in Curtright [35], Aulakh et al. [105], Labastida and Morris [115], Hull [37], and Hull [38] that the physical degrees of freedom of the dual graviton in D = 5 are massless, and its dynamical variables are represented by spatial, transverse and traceless components ${\tilde{h}}_{ijk}$ of the Curtright field ${\tilde{h}}_{\mu \nu \rho }$, which have the Young symmetry similar to ${\tilde{h}}_{\mu \nu \rho }$, and transform in the little group SO(D − 2). There are the spatial dual Einstein tensor ${\tilde{G}}_{ijk}$ and the spatial dual Riemann curvature ${\tilde{R}}_{ijrsm}$ which are constructed by the spatial tensor ${\tilde{h}}_{ijk}$. Moreover, the dynamical variables of the standard graviton, which is dual to the Curtright field ${\tilde{h}}_{\mu \nu \rho }$ in D = 5, are given by spatial, transverse and traceless components h_ij of the Pauli-Fierz field h_μν, which is symmetric similar to h_μν. Similarly, there are the spatial Einstein tensor G_ij and the spatial Riemann curvature R_ijrs which are constructed by the spatial tensor h_ij.

Let us consider the electric and magnetic fields of the standard graviton, which are constructed from the spatial Riemann curvature [43]:

where ${{E}}_{ijmn}\left[h\right]$ has the Young symmetry , ${{B}}_{mni}\left[h\right]$ and has the Young symmetry .

We also build the electric and magnetic fields of the dual graviton from the spatial dual Einstein tensor and the spatial dual Riemann curvature, respectively [43]:

where ${\tilde{{E}}}_{ijm}[\tilde{h}]$ has the Young symmetry , ${\tilde{{B}}}_{ijmn}[\tilde{h}]$ and has the Young symmetry .

The electric fields ${{E}}_{ijmn}\left[h\right]$ and ${\tilde{{E}}}_{ijm}[\tilde{h}]$ are double-traceless and traceless, respectively, which correspond to G₀₀ = 0 and ${\tilde{G}}_{0j0}=0$. There are similar properties for the magnetic fields ${{B}}_{mni}\left[h\right]$ and ${\tilde{{B}}}_{ijmn}[\tilde{h}]$:

The electric fields, ${{E}}_{ijmn}\left[h\right]$ and ${\tilde{{E}}}_{ijm}[\tilde{h}]$, and the magnetic fields, ${{B}}_{mni}\left[h\right]$ and ${\tilde{{B}}}_{ijmn}[\tilde{h}]$, have the following identities

which are equivalent to the Ricci conditions R_0j = 0 and ${\tilde{R}}_{0jm}=0$.

The Bianchi identities imply that the electric fields, ${{E}}_{ijmn}\left[h\right]$ and ${\tilde{{E}}}_{ijmn}[\tilde{h}]$, and magnetic fields, ${{B}}_{mni}\left[h\right]$ and ${\tilde{{B}}}_{ijmn}[\tilde{h}]$, are similarly transverse:

The electric fields ${{E}}_{ijmn}\left[h\right]$ and ${\tilde{{E}}}_{ijm}[\tilde{h}]$ transform under the mixed symmetries (2,2) and (2,1), while the magnetic fields ${{B}}_{mni}\left[h\right]$ and ${\tilde{{B}}}_{ijmn}[\tilde{h}]$ transform under the mixed symmetries (2,1) and (2,2). From the twisted self-duality conditions [43], it follows that

or in a duality-symmetric way

with matrix notations

where the SO(2) duality matrix ${S}$ is defined by Equation (38). Therefore, the electric and magnetic fields of the standard graviton are fully equivalent to the magnetic and electric fields of the dual graviton in D = 5 under SO(2) electric-magnetic duality rotations (see [43] for constraint and dynamical formulas).

2.3. D = 11: Mixed Symmetry (8, 1) Field

In the case of D = 11 spacetime, which are relevant to maximal supergravity/M-theory, the dual graviton defined by the first dual representation is associated with a tensor field ${\tilde{h}}_{a_1···a_8|b}$ of Young symmetry (8, 1). Interestingly, the conjectured hidden symmetry E₁₁ of M-theory is decomposed into GL(11) subalgebras: a mixed symmetry (8, 1) tensor (dual graviton), a 3-form, a 6-form, and other mixed symmetry fields [44]. It was shown that the dynamics and hidden symmetries of gravity are strongly linked to Lorentzian Kac–Moody algebras [116]. Moreover, the Weyl groups of infinite-dimensional Kac–Moody algebras (see [117] for review) are compatible with the groups $E_{11}(=E_8^{+++})$ [118–120] and $E_{10}(=E_8^{++})$ [121, 122], which contain information about the gravitational electric-magnetic duality, as well as the structures of M-theory (see [123] for review).

The Dynkin diagram of the Lorentzian Kac-Moody algebra $E_{11}=E_8^{+++}$ is depicted below (see e.g., [44, 124–126]):

which encodes underlying hidden symmetries of M-theory [44, 124] (the same for $E_{10}=E_8^{++}$ [127]). The various exceptional Lie groups (E₆, …, E₁₀) are embedded in the infinite-dimensional Kac–Moody algebra E₁₁, i.e., E₆ ⊂ ··· ⊂ E₁₀ ⊂ E₁₁. The infinite-dimensional Kac–Moody algebra E₁₁ (also E₁₀) can be constructed from E₈ through extensions of E₈ with three extra nodes (two extra nodes in E₁₀), so we derive the Lorentzian Kac–Moody algebra $E_8^{+++}=E_{11}$ (also $E_8^{++}=E_{10}$) [117].

The Kac–Moody algebra E₁₁ can be decomposed into the GL(11) subalgebras by deleting the node 11 in the E₁₁ Dynkin diagram (see the above diagram) [44, 46, 128]. The decomposition subalgebras correspond to the low level E₁₁ tensor fields in the non-linear realization of E₁₁ and its vector, E₁₁ ⊗_s l₁,

The zero- and third-level fields, h_a^b and ${\tilde{h}}_{a_1···a_8|b}$, correspond to the graviton and the dual graviton in D = 11, respectively. The first-level bosonic 3-form field, A_α1α2α3 is related to non-gravitational degrees of freedom of M-theory. The second-level 6-form field, A_a1···a6, has equations of motion, which can be dual to those of the 3-form field A_a1a2a3, and provides another way to describe the degrees of freedom of A_a1a2a3. These fields lead to at least one spacetime coordinate for each in the E₁₁ ⊗_s l₁ non-linear realization [125, 129],

The spacetime coordinate x^a, which corresponds to the graviton, constructs the spacetime curvature for the dynamics of gravity. It is seen that the 3-form field, A_a1a2a3, and 6-form field, A_a1···a6, are associated with the 2-form and 5-form coordinates, respectively. The mixed symmetry (8, 1) tensor field, ${\tilde{h}}_{a_1···a_8|b}$, which is dual to the graviton in D = 11, is related to the 8-form coordinate and the mixed symmetry (7, 1) coordinate. The dual graviton field and its equation of motion possess the following identities [130]

where the equations of motion $E_{{\alpha }_1···{\alpha }_8|\mu }^{(2)}$ is of Young symmetry type (8, 1), and the numerical superscript describes the number of spacetime derivatives (see [129, 130] for more details of the E₁₁ equations of motion), i.e., in empty space

while the equations of motion for the graviton are [129]:

where ω_αβ|γ is defined as (h_a^b in the E₁₁ ⊗_s l₁ non-linear realization) [129]:

The equations of motion for the non-gravitational fields A_α1α2α3 and A_α1···α6 are also given by [129, 130]

There is a unique E₁₁ invariant equation with one derivative, which is obtained from the non-linear realization [129], and it contains the graviton and its dual field:

The non-gravitational fields A_a1a2a3 and A_a1···a6 possess a unique E₁₁ invariant equation with one derivative (see [126, 131] for details):

Variations of the E₁₁ equations of motion (82 ) and (83) result in $E_{ab}^{(2)}$ and $E_{a_1{a}_2{a}_3}^{(2)}$, with the duality relations of $E_{a_1···a_8|b}^{(2)}$ and $E_{a_1···a_6}^{(2)}$, respectively [129]:

From the unique E₁₁ invariant Equation (82), $E_{ab}^{(1)}{}^{|c}\doteq 0$, we get the linearized Einstein equation, $E_a^{(2)}{}^b=0$, and the equation of motion for the 11-dimensional dual graviton, $E_{a_1···a_8|b}^{(2)}=0$. While from the unique E₁₁ invariant Equation (83), one deduces the equations of motion $E_{a_1{a}_2{a}_3}^{(2)}=0$, and its dual equations of motion $E_{a_1···a_6}^{(2)}=0$. Therefore, the algebra E₁₁ yields a network of equations of motion, including the typical equations of motion in general relativity.

2.4. Generalized Dual Spin-2 Fields

As mentioned at the beginning of section 2, the Pauli-Fierz field associated with the spin-2 field h_αβ is dual to a field dualized on one index (dual graviton) or on both indices (double-dual graviton) [38, 96]. We consider only its dualization on one index since it presents equations of motion equivalent to the linearized Einstein equations and its action satisfies Lorentz-invariance [40]. Hence, the generalized, free massless, dual spin-2 fields ${\tilde{h}}_{\left[{\alpha }_1···{\alpha }_{D-3}\right]\beta }\equiv {\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\beta }$ in arbitrary dimensions (D ≥ 4) can be given by Young symmetry type (D − 3, 1) having the Young diagram [38, 43]:

which possesses the following properties

and has (D − 3)(D + 1)!/3(D − 2)! components in D dimensions [41].

The action associated with the equations of motion of free massless, dual spin-2 fields ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}\beta }$ in D-dimensional Minkowski spacetime explicitly reads [41, 47, 105]⁴

It may also be written in terms of a field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\beta }$, in a similar manner of the Curtright action (47), as follows [132–134]⁵:

where the “generalized Curtright” field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\beta }$, a general form of (48), is a tensor with Young symmetry type (D − 2, 1) with the diagram:

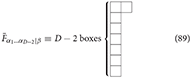
defined as

For D = 4 and 5, the Lagrangian (87) recovers the Pauli-Fierz (13) formulated by ${\tilde{h}}_{\mu \nu }$ and the Curtright action (46), respectively. For D = 5, the Lagrangian (88) also becomes the Curtright action (47).

The action (87) is invariant under the following gauge transformation [38, 41, 134]

where χ_{α1···αD − 4|β} and α_{α1···αD − 3} are mixed symmetry type (D − 4, 1) and antisymmetric (D − 3)-rank tensors, respectively:

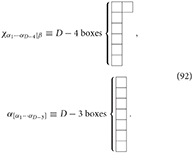
The action (88) is also invariant under the gauge transformation (91) (see [132, 133]). The field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\beta }$ defined by (90) is not gauge invariant, but it is transformed as

The gauge transformations for χ_{α1···αm−1|β} = χ_{[α1···αm−1]β} and α_α1···αm = α_{[α1···αm]} (m = D − 3 at the initial level) are reducible to an arbitrary mixed symmetry type (m − 2, 1) tensor χ_{α1···αm−2|β} = χ_{[α1···αm−2]β} and an arbitrary antisymmetric (m − 1)-rank tensor α_{α1···αm−1} = α_{[α1···αm−1]} for m > 3 (see [115] for irreducible representations):

For m = 3, they are reduced to an arbitrary symmetric tensor σ_μν = σ_(μν) and an arbitrary antisymmetric tensor α_μν = α_[μν],

The gauge transformations for σ_μν and α_μν are also reducible to an arbitrary vector field σ_μ,

The gauge symmetry for σ_μ is irreducible.

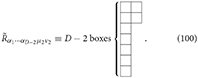
The linearized dual Riemann curvature tensor in D dimensions is defined as

which is of Young symmetry (D − 2, 2):

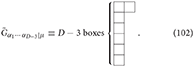
Similarly, the D-dimensional dual Einstein equations are

where the D-dimensional dual Einstein tensor ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu }$ is of mixed symmetry type (D − 3, 1) with the Young diagram:

The D-dimensional dual Ricci tensor is defined by

where the dual Ricci tensor is of Young symmetry (D − 3, 1).

2.5. Gravitationally Magnetic-type Source

The introduction of magnetic monopoles to Maxwell theory requires that the magnetic charge q_m is related to the electric charge q_e through the so-called Dirac quantization condition [1, 2]

which is invariant under the SO(2) electric-magnetic duality rotations,

A singularity of the magnetic field or a Dirac string is unobservable in the spin-1 field if the condition (104) is imposed on the magnetic charge.

Similarly, there is a quantization condition for the spin-2 field such as gravity [91]:

where the quantities p_μ and ${\tilde{p}}^{{}_{\mu }}$ are 4-momenta of linearized diffeomorphisms associated with the ordinary (electric-type) and magnetic-type matters, respectively. For a massive particle, we get p_μ = mu_μ and ${\tilde{p}}^{\mu }=\tilde{m}{ũ}^{\mu }$, where m is the ordinary (electric-type) mass, u_μ is the 4-velocity of the electric-type source, $\tilde{m}$ is the magnetic-type mass, and ũ^μ is the 4-velocity of the magnetic-type source.

It is important to note that the Dirac quantization condition (Equation 104) is applied to the charges in the spin-1 case, whereas the spin-2 quantization condition (Equation 106) is imposed on 4-momenta, not the mass. In the rest frame, we get a quantization condition:

where E is the ordinary (electric-type) energy, and Ẽ is the magnetic-type energy. Hence, we get the energy quantization condition [91, 135, 136] (see also [77, 78, 137] for a quantization condition for ordinary mass and gravitomagnetic mass).

The Einstein equations coupled to the gravitating source are

which are equivalent to

where T^μν is the energy-momentum tensor of the ordinary (electric-type) matter.

In section 2.1, it was shown that the Pauli-Fierz field equations are duality invariant in D = 4, so the Einstein tensor ${\tilde{G}}^{\mu \nu }$ for the dual gravity ${\tilde{h}}_{\mu \nu }$ can be coupled to the magnetic-type energy-momentum tensor ${\tilde{T}}^{\mu \nu }$ as follows:

or equivalently to the dual Ricci curvature:

The electric-magnetic duality rotations (Equations 41, 42) of the curvatures imply that there are the SO(2) rotations of the electric-type and magnetic-type energy-momentum tensors:

Hence, the Einstein equations are invariant under the electric-magnetic duality in D = 4.

Considering D-dimensional spacetime, the linearized Einstein equations become

which are equivalent to [38]:

where T_μν is the energy-momentum tensor of the electric-type source.

The conservation laws for the electric-type and magnetic-type sources impose that ${\partial }^{\nu }{T}_{\mu \nu }=0$ and ${\partial }^{\nu }{\tilde{T}}_{\mu \nu }=0$, so the motion of a massive particle should follow straight lines. For a massive particle, one can write

where w_ν and ${\tilde{w}}_{\nu }$ represent the electric- and magnetic-type worldlines, respectively, u_μ = dw_μ/ds and ${ũ}_{\mu }=d{\tilde{w}}_{\mu }/ds$ are the 4-velocities of the electric- and magnetic-type sources, and m and $\tilde{m}$ the electric- and magnetic-type masses, respectively. The quantity s is spacelike, and τ is timelike. From Equations (116, 117), one obtains $T_{\mu \nu }={\delta }^{(3)}(\overrightarrow{x}-\overrightarrow{w}(x^0))u_{\mu }{u}_{\nu }/u_0$ and ${\tilde{T}}_{\mu \nu }={\delta }^{(3)}(\overrightarrow{x}-\overrightarrow{\tilde{w}}(x^0)){ũ}_{\mu }{ũ}_{\nu }/{ũ}_0$.

Dirac strings in D = 4 can be constructed as follows. Let decompose the linearized Riemann curvature R_μναβ into the massless part and the massive part,

The massless part r_μναβ satisfies the cyclic and Bianchi identities (r_[μνα]β = 0 and ∂_[ρr_μν]αβ = 0), and the massive part m_μναβ is coupled to the magnetic-type source

where ${\tilde{M}}_{\alpha \mu \nu }$ defines the magnetic-type source as

and ${\tilde{M}}_{\alpha \beta \mu }={\tilde{M}}_{\left[\alpha \beta \right]\mu }\equiv {\tilde{M}}_{\alpha \beta |\mu }$ is a tensor with the mixed symmetry type (2, 1).

There is a symmetric tensor h_μν that satisfies

If we define $y^{\alpha \beta }{}_{\mu }={ϵ}^{\alpha \beta \gamma \lambda }{\partial }_{\gamma }{h}_{\lambda \mu }$, where $y^{\alpha \beta }{}_{\mu }=y^{[\alpha \beta ]}{}_{\mu }$ is a mixed symmetry type (2, 1) tensor (${\partial }_{\alpha }{y}^{\alpha \beta }{}_{\mu }=0$), the linearized Riemann curvature R_μναβ can be rewritten as

Defining $Y_{\mu \nu \alpha }=y_{\mu \nu \alpha }+{\tilde{M}}_{\mu \nu \alpha }$ (where Y_μνα = Y_[μν]α) yields

The tensor ${\tilde{M}}_{\alpha \beta |\mu }$ defined by (120) can be written using a Dirac string y^μ(τ, θ) attached to the magnetic-type source, $y^{\mu }(\tau ,0)={\tilde{w}}^{\mu }(\tau )$ in (117). One can take [91]

From Equations (117) and (124), it can be seen that the divergence of ${\tilde{M}}_{\alpha \beta |\mu }$ is identical with ${\tilde{T}}_{\mu \nu }$ (by a factor of $16\pi G_{\text{N}}^{(4)}/c^4$). The momentum $\tilde{m}{ũ}_{\mu }$ of the magnetic-type source by its mass $\tilde{m}$ and 4-velocity ũ_μ is therefore conserved.

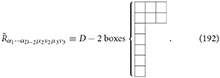
Similarly, the linearized Einstein equations of the dual graviton ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\beta }$ in D dimensions with the magnetic-type source read

where ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\beta }$ is the dual Einstein tensor, ${\tilde{T}}_{{\alpha }_1{\alpha }_2···{\alpha }_{D-3}|\beta }$ is the energy-momentum tensor of the magnetic-type source in D-dimensional spacetime, both ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\beta }$ and ${\tilde{T}}_{{\alpha }_1{\alpha }_2···{\alpha }_{D-3}|\beta }$ are tensors with the mixed symmetry type (D − 3, 1).

The linearized dual Einstein Equations (125) are equivalent to

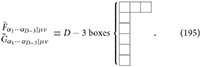
where ${\tilde{R}}_{{\alpha }_1{\alpha }_2···{\alpha }_{D-2\mu \nu }}$ is the linearized dual Riemann curvature defined by Equation (10).

In the little group SO(D − 2), the Einstein tensor and its dual tensor in D dimensions satisfy (see [38, 138] for further discussions):

If the magnetic-type energy-momentum tensor satisfies

where M_{i2···iD − 3j} is an arbitrary tensor with the mixed symmetry type (D − 4, 1), and the electric-type energy-momentum tensor can be written as follows:

so the magnetic-type source is correlated to the Hodge dual of the electric-type source:

The magnetic-type energy-momentum tensor ${\tilde{T}}_{i_1···i_{D-3}|j}$ can be a source for the gravitational Bianchi identity [38]

Similarly, the energy-momentum tensor T_ij is a source for the Bianchi identity of the dual Riemann curvature [38]

It can be seen that the Einstein Equations (127, 128), and the Bianchi identities (133) and (134) are invariant under the twisted self-dual conditions discussed in section 2.1. We can express their electric-magnetic duality transformations using matrix notations

where the SO(2) electric-magnetic duality matrix ${S}$ is defined by Equation (38), 𝔗 and ℜ represent the D-dimensional energy-momentum tensor and Ricci curvature associated with both the electric-type and magnetic-type sources, respectively,

and ^⋆𝔗 and ^⋆ℜ represent their corresponding Hodge isomorphisms,

It means that the equations of motion for the D-dimensional dual graviton ${\tilde{h}}_{i_1···i_{D-3}|j}$ are equivalent to those for the graviton h_ij under the SO(2) electric-magnetic invariance.

2.6. Spin-2 Harmonic Condition

In this section, we introduce the harmonic coordinate condition, which makes it possible to propagate gravitational waves (${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$) in linearized gravity. We will see that the harmonic condition is equivalent to divergenceless and nonvanishing curl of the electric and magnetic parts of the linearized Weyl tensor encoded by the Pauli-Fierz field h_μν in the instantaneous rest-space of an observer moving in flat spacetime (defined by Equations 27, 28).

We consider the vacuum Einstein equations in the linearized flat condition (R_μν = 0 and R = 0), which imply

Equation (138) presents a second-order equation for the Pauli-Fierz field h_μν. To have a wave equation for the Pauli-Fierz field, ${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$, it is required to have a constraint, the so-called De Donder gauge condition [103]:

Substituting Equation (141) into (138) leads to the wave equation ${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$.

We can have some constraints along a four-velocity vector u^μ in the rest-space of a local co-moving observer in Minkowski spacetime:

From Equation (140), the electric and magnetic parts of the linearized Weyl tensor in the vacuum Einstein equations become

Taking a covariant divergence from the gravitoelectric field (145) and the gravitomagnetic field (146), and using constraints (Equations 142 –144), one obtains the covariant divergenceless condition for the gravitoelectric and gravitomagnetic fields:

In Minkowski spacetime, the covariant derivative of a spatial, traceless symmetric 2nd-rank tensor is decomposed into the time derivative along with a four-velocity vector u^μ and the spatial derivative, ${\partial }^{\mu }{E}_{\mu \nu }=-u^{\mu }{(E_{\mu \nu })}^{\prime }+{\text{D}}^{\mu }{E}_{\mu \nu }$ (see e.g., [66]). As the gravitoelectric and gravitomagnetic tensor are spatial ($E_{\mu \nu }{u}^{\nu }=0=B_{\mu \nu }{u}^{\nu }$), one gets $u^{\mu }{(E_{\mu \nu })}^{\prime }=0=u^{\mu }{(B_{\mu \nu })}^{\prime }$, so we get the spatial divergenceless condition (${\text{D}}^{\mu }{E}_{\mu \nu }=0={\text{D}}^{\mu }{B}_{\mu \nu }$), which were previously proven for gravitational waves in the 1+3 covariant formalism [66, 139, 140].

It can easily be verified that the covariant curl and distortion of the gravitoelectric field (145) and the gravitomagnetic field (146) do not vanish under the De Donder gauge condition and the linearized flat condition:

where the covariant curl is defined as $\mathfrak{c}\mathfrak{u}\mathfrak{r}\mathfrak{l}{(E)}_{\mu \nu }\equiv {ϵ}_{\rho \lambda (\mu }{\partial }^{\rho }{E}_{\nu )}{}^{\lambda }$. The nonvanishing covariant curl and distortion conditions are equivalent to the nonzero, spatial curls and distortions of E_μν and B_μν for gravitational waves in the 1 + 3 covariant formalism [66, 67, 141]: curl(E)_μν ≠ 0 ≠ curl(B)_μν and D_ρE_μν ≠ 0 ≠ D_ρB_μν, where the spatial curl is defined using the spatial derivative D_μ as $\mathrm{curl}{(E)}_{\mu \nu }\equiv {ϵ}_{\rho \lambda (\mu }{\text{D}}^{\rho }{E}_{\nu )}{}^{\lambda }$. From Equations (147, 148), the wave equation of the Pauli-Fierz field h_μν in empty space, ${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$, corresponds to ${\partial }^{\rho }{\partial }_{\rho }{E}_{\mu \nu }=0={\partial }^{\rho }{\partial }_{\rho }{B}_{\mu \nu }$ in the linearized theory, which are equivalent to ${\text{D}}^2{E}_{\mu \nu }-{(E_{\mu \nu })}^{\prime \prime }=0={\text{D}}^2{B}_{\mu \nu }-{(B_{\mu \nu })}^{\prime \prime }$ in the 1 + 3 covariant formalism [60, 66]. Hence, the De Donder gauge condition in the vacuum Einstein equations allows the propagation of the spin-2 waves, ${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$, and imposes divergenceless and nonvanishing-curl of the gravitoelectric and gravitomagnetic fields encoded by the Pauli-Fierz field (Equations 27 and 28) of the linearized theory in Minkowski spacetime.

To satisfy the De Donder gauge condition (141), the Pauli-Fierz field could be assumed to be transverse, traceless, and spatial (e.g., [39]):

which is called the transverse–traceless gauge condition, and allows the propagation of a massless, spin-2 field in Minkowski flat spacetime.

In the case of the transverse–traceless gauge condition (149), the harmonic, massless spin-2 field of the wave equations (see e.g., [39]) in the momentum space $m_{\mu }=(|\overrightarrow{m}|,\overrightarrow{m})$ reads

where h⁺ and h^× are the helicity states associated with the + and × polarization states of the Pauli-Fierz field h_μν (graviton), $e_{\mu \nu }^{+}=x_{\mu }{x}_{\nu }-y_{\mu }{y}_{\nu }$ and $e_{\mu \nu }^{\times }=x_{\mu }{y}_{\nu }+y_{\mu }{x}_{\nu }$ are the + and × polarization tensors, $x_{\mu }=(0,\widehat{x})$ and y_μ = (0, ŷ) are spatial 4-vectors satisfying $\widehat{x}·\widehat{x}=1=ŷ·ŷ$ and $\widehat{x}·ŷ=0$ with $\widehat{x}·\widehat{m}=0=$ $ŷ·\widehat{m}$ making an orthogonal triad $ŷ=\widehat{x}\times \widehat{m}$ (i.e., $\widehat{x}=-ŷ\times \widehat{m}$) where $\widehat{m}=\overrightarrow{m}/\left|\overrightarrow{m}\right|$.

Since the equations of motion for the Pauli-Fierz field h_μν are fully equivalent to the dual Pauli-Fierz field ${\tilde{h}}_{\mu \nu }$ under SO(2) electric-magnetic duality rotations, we have the following expression for the dual Pauli-Fierz field ${\tilde{h}}_{\mu \nu }$ in D = 4:

where ${\tilde{h}}^{+}$ and ${\tilde{h}}^{\times }$ are the helicity states associated with the + and × polarization states of the dual Pauli-Fierz field ${\tilde{h}}_{\mu \nu }$(dual graviton).

Considering the first dual formulation, and taking a 2-D permutation ϵ_μν from the expression (150) yields ${\tilde{h}}_{\mu \nu }(m)=h^{+}(m){ϵ}_{\mu }{}^{\rho }{e}_{\rho \nu }^{+}(m)+h^{\times }(m){ϵ}_{\mu }{}^{\rho }{e}_{\rho \nu }^{\times }(m)$. As the spatial vectors $\widehat{x}$ and ŷ making an orthogonal triad with $\widehat{m}$, one gets ${ϵ}_{\mu }{}^{\rho }{x}_{\rho }(m)=y_{\mu }(m)$ and ${ϵ}_{\mu }{}^{\rho }{y}_{\rho }(m)=-x_{\mu }(m)$ in the momentum space m_μ (equivalent to $\widehat{x}$ × $\widehat{m}$ = ŷ and $ŷ\times \widehat{m}=-\widehat{x}$), so we get ${ϵ}_{\mu }{}^{\rho }{e}_{\rho \nu }^{+}(m)=e_{\mu \nu }^{\times }(m)$ and ${ϵ}_{\mu }{}^{\rho }{e}_{\mu \nu }^{\times }(m)=-e_{\mu \nu }^{+}(m)$:

by comparison with Equation (150), the dual helicity states in the momentum space have the following rotations:

which is similar to Equation (34). We see that the + and × helicity states of the graviton h_μν and the dual graviton ${\tilde{h}}_{\mu \nu }$ are fully equivalent to each others under the following twisted self-dual condition in the momentum space:

with ${S}$ defined by (38), and matrix notations of the helicity states:

which is analogous with the twisted self-dual conditions (35). We can also show that the helicity states of the graviton h_μν is rotated into those of the dual graviton ${\tilde{h}}_{\mu \nu }$ under the duality transformations:

Thus, the + and × helicity states of wave equations for the dual graviton (${\partial }^{\rho }{\partial }_{\rho }{\tilde{h}}_{\mu \nu }=0$) are respectively rotated to the × and + helicity states of gravitational waves (${\partial }^{\rho }{\partial }_{\rho }{h}_{\mu \nu }=0$) under SO(2) electric-magnetic duality rotations in D = 4, and are duality invariant under the twisted self-dual condition.

3. Spin-3 Field and Its Dual Fields

We now introduce the spin-3 field, as a step toward the spin-s generalization. The typical spin-3 field in D-dimensional spacetime is represented by a symmetric 3rd rank tensor h_μνρ = h_(μνρ) with Young symmetry (1, 1, 1) and the diagram . The equations of motion of h_μνρ (the ordinary spin-3 field) in D-dimensional flat spacetime can be described using the Fronsdal action [102] for the spin-3 case

where the Lagrangian ${L}\left[h_{\mu \nu \rho }\right]$ is as follows [47, 142, 143]

The Fronsdal Lagrangian (159) is a generalization of the Pauli-Fierz theory on the spin-3 field, and is invariant under the gauge transformation

where the gauge parameter ξ_μν = ξ_(μν) is an arbitrary symmetric 2rd rank field.

By analogy with the Einstein equations, one can write the spin-3 Einstein equations in D dimensions (see [91] for the generalized Einstein equations):

where the spin-3 Einstein tensor G_μ1μ2μ3 = G_(μ1μ2μ3) is a traceless ($G_{\mu \rho }{}^{\rho }=0$), symmetric tensor with the Young diagram . The tensor G_μ1μ2μ3 can be written in terms of the so-called Fronsdal [102] tensor F_μ1μ2μ3 for the spin-3 case as follows

where the spin-3 Fronsdal tensor F_μ1μ2μ3 = F_(μ1μ2μ3) is a symmetric tensor with the diagram , defined by

which is related to the spin-3 Ricci tensor

where the spin-3 Ricci tensor R_{μ1ν1|μ2μ3} is a 4th-rank tensor with the mixed symmetry (2, 1, 1) having the Young diagram , and the spin-3 Riemann tensor R_{μ1ν1μ2ν2μ3ν3} is a 6th-rank tensor with the mixed symmetry (2, 2, 2) having the Young diagram .

For spin-3 fields, we can define the first dual representation in a similar manner of the dual definitions for the spin-2 field, i.e., Equations (3, 4) [38, 89, 98]. The first dual field of the spin-3 field h_μνρ = h_(μνρ) in D-dimensional spacetime is dualized on one index only. For the physical gauge spin-3 field h_ijk, we have in the little group SO(D − 2) [38]:

with the following properties [38]:

The first dual spin-3 field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}\mu \nu }$ is then described by a tensor with Young symmetry (D − 3, 1, 1) having the Young diagram:

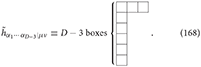
For spin-3 fields, we may also define the second dual formulation in a similar manner of the spin-2 dual field (6) and (7)⁶. In the second dual formulation, the physical gauge spin-3 field h_ijk in D-dimensional spacetime is dualized on two indices:

having the following properties:

The second dual spin-3 field ĥ_{α1···αD − 3β1···βD − 3ρ} is described by a tensor with the mixed symmetry (D − 3, D − 3, 1) having the Young diagram:

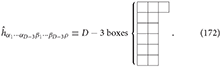
It might be possible to define a third dual field of the spin-3 field, which is dualized on all three indices. The physical gauge spin-3 field h_ijk in D dimensions can be dualized in the little group SO(D − 2) as follows:

having the following properties:

The third dual spin-3 field ${\stackrel{⌣}{h}}_{{\alpha }_1···{\alpha }_{D-3}{\beta }_1···{\beta }_{D-3}{\gamma }_1···{\gamma }_{D-3}}$ is described by a tensor with the mixed symmetry (D − 3, D − 3, D − 3).

In particular, we notice that there are two different dual formulations for the spin-2 field in section 2, whereas three different dual formulations for the spin-3 field exist. In D = 4, all three dual formulations correspond to a symmetric 3rd rank tensor ${\tilde{h}}_{\mu \nu \rho }={\tilde{h}}_{(\mu \nu \rho )}$ with the Young diagram . Thus, we get only one dual formulation of the spin-3 field in 4-dimensional spacetime.

The second dual physical gauge field ĥ and the third dual physical gauge field $\stackrel{⌣}{h}$ can be written in terms of the first dual physical gauge field $\tilde{h}$ and second dual physical gauge field ĥ, respectively, and one can recover the first dual physical gauge field $\tilde{h}$ from the second and third dual physical gauge field in the little group SO(D − 2). Nevertheless, the action principle of the second field $\tilde{h}$ and third dual field $\stackrel{⌣}{h}$ in D dimensions higher than 4 may not follow from a Lorentz-invariance action (similar to the argument made for the spin-2 field [40]), so the first dual field formulation, which is dualized on one index only, is considered in the following parts of this section.

The Fronsdal theory for the spin-3 case in D = 4 is dualized to a Fronsdal action $S=\int d^{4}x{L}\left[{\tilde{h}}_{\mu \nu \rho }\right]$ where the Lagrangian ${L}\left[{\tilde{h}}_{\mu \nu \rho }\right]$ is formulated in terms of a symmetric massless 2nd-rank tensor ${\tilde{h}}_{\mu \nu \rho }={\tilde{h}}_{(\mu \nu \rho )}$ (dual spin-3 field), similar to Equation (159) with the gauge transformation ${\delta }_{\xi }{\tilde{h}}_{\mu \nu \rho }=3{\partial }_{(\mu }{\tilde{\xi }}_{\nu \rho )}$ where ${\tilde{\xi }}_{\mu \nu }$ is a arbitrary, symmetric 2nd rank tensor.

3.1. D = 5: Mixed Symmetry (2, 1, 1) Field

The dual field of the spin-3 field h_μνλ in 5-dimensional spacetime is represented by ${\tilde{h}}_{\alpha \beta |\mu \nu }$, which is a tensor with Young symmetry (2, 1, 1) with the diagram:

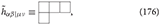
and satisfies:

The equations of motion of a free massless spin-3 field ${\tilde{h}}_{\alpha \beta |\mu \nu }$ in 5-dimensional Minkowski spacetime η_μν = diag(−, +, +, +, +) is represented by the following action principle [47] ⁷

which satisfies the gauge symmetry

where χ_μνρ = χ_(μνρ) is an arbitrary symmetric tensor with Young symmetry (1, 1, 1) ≡ , and φ_μν|ρ = φ_[μν]ρ is an arbitrary tensor with Young symmetry (2, 1) ≡ (see also gauge transformations in [47, 143]). The gauge transformations for χ_μ|νρ and φ_μν|ρ are reducible:

The parameters σ_μν = σ_(μν) and α_μν = α_[μν] are symmetric and antisymmetric arbitrary tensors, respectively, and their gauge transformations are reducible:

The parameter σ_μ is an arbitrary vector field, and its gauge transformation is irreducible.

3.2. D > 5: Young Symmetry (D − 3, 1, 1) Fields

The D-dimensional spin-3 field h_αβρ can be dualized to a free massless spin-2 fields ${\tilde{h}}_{\left[{\alpha }_1···{\alpha }_{D-3}\right]\mu \nu }\equiv {\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ with Young symmetry type (D − 3, 1, 1) defined by (Equation 165, 166), and satisfying

This is associated with the dualization on one index only, which provides equations of motion with a Lorentz invariant action. The equations of motion of free massless, dual spin-3 fields ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\beta \rho }$ in D-dimensional flat spacetime are represented by the action principle [47]:

which satisfies the gauge symmetry

where χ_{α1…αD − 4|μν} = χ_{[α1…αD − 4]μν} = χ_{α1…αD − 4(μν)} is an arbitrary tensor with the mixed symmetry (D − 4, 1, 1), and φ_{α1…αD − 3|μ} = φ_{[α1…αD − 3]μ} is an arbitrary tensor with the mixed symmetry (D − 3, 1). The gauge transformations for χ_{α1…αD − 4|μν} and φ_{α1…αD − 3|μ} are reducible.

The action (185) is also invariant under the following gauge symmetry [47]:

where χ_{α1…αD − 4|μν} is a tensor with the mixed symmetry (D − 4, 1, 1), and its gauge transformation is reducible.

In a similar way of the Curtright action (47) and the generalized Curtright action (88), one may write the action of the dual spin-3 field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ using a “spin-3 Curtright” field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\mu \nu }$ defined as

is a tensor with Young symmetry type (D − 2, 1, 1):

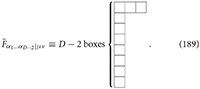
The spin-3 Curtright action should be invariant under the gauge symmetry (186), however, the field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\mu \nu }$ is not gauge invariant. The field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\mu \nu }$ has the following transformation

Note that the Curtright field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|\mu \nu }$ defined by Equation (188) should be not mistaken with the Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ defined by (198) in this section.

The spin-3 dual Riemann tensor defined as

is a tensor with Young symmetry (D − 2, 2, 2) and the diagram:

For a free, massless dual spin-3 field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$, one can write the spin-3 dual Einstein equations similar to the spin-2 case [38]:

where the spin-3 dual Einstein tensor ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ is of Young symmetry type (D − 3, 1, 1), and traceless (${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }{\eta }^{\mu \nu }={\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }{\eta }^{{\alpha }_{D-3}\nu }=0$) with the following definition:

where both the spin-3 dual Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ and the spin-3 dual Einstein tensor ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ are of Young symmetry type (D − 3, 1, 1), and the diagram

The spin-3 dual Ricci tensor can also be defined by

where the spin-3 dual Ricci tensor is of Young symmetry (D − 2, 1, 1), and defined in term of the dual Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ as follows:

The dual Ricci tensor ${\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}|\mu \nu }$ is antisymmetrized in α₁···α_{D − 2} and symmetrized in μν, i.e., ${\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}|\mu \nu }={\tilde{R}}_{\left[{\alpha }_1···{\alpha }_{D-2}\right]\mu \nu }={\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}(\mu \nu )}$.

The Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|{\mu }_1{\mu }_2}$ can be written in term of the dual spin-3 field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ as follows:

The dual Einstein tensor ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ and the dual Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ for the spin-3 field are antisymmetrized in indices α₁···α_{D − 3} and symmetrized in indices μν, i.e., ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }={\tilde{G}}_{\left[{\alpha }_1···{\alpha }_{D-3}\right]\mu \nu }={\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}(\mu \nu )}$ and ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }={\tilde{F}}_{\left[{\alpha }_1···{\alpha }_{D-3}\right]\mu \nu }={\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}(\mu \nu )}$.

3.3. Spin-3 Magnetic-Type Source

The spin-3 field (h_μνρ ≡ h_(μνρ)) can be coupled to the spin-3 electric-type source T_μνρ ≡ T_(μνρ) [38, 91]. For the spin-3 Riemann tensor R_{μ1ν1μ2ν2μ3ν3}, one can write the field equations in D-dimensional spacetime as follows

where the spin-3 Ricci tensor R_{μ1ν1|μ2μ3} = R_{[μ1ν1]μ2μ3} = R_{μ1ν1(μ2μ3)} is a tensor with mixed symmetry (2, 1, 1), defined by (164), and ${{T}}_{\mu \nu \rho }={{T}}_{(\mu \nu \rho )}$ is a traceless (${\mathcal{T}}_{\mu \rho }{}^{\rho }=0$), symmetric 3rd rank tensor defined by removing the traces $T_{\mu \rho }{}^{\rho }$ from the energy-momentum tensor T_μνρ:

By analogy with the Einstein equations, one can write an equivalence of Equation (199):

which can be considered as the spin-3 Einstein equations with the spin-3 electric-type source (see [91] for spin-s generalization of the Einstein equations).

The dual Einstein tensor (193) for the dual spin-3 field can be coupled to the spin-3 magnetic-type source:

where the spin-3 dual stress-energy tensor ${\tilde{{T}}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ is a traceless $({\tilde{{T}}}_{{\alpha }_2···{\alpha }_{D-3}\rho |}{}^{\nu \rho }=0)$, tensor with Young symmetry type (D − 3, 1, 1) and defined as

where ${\tilde{T}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ is the spin-3 dual stress-energy, and has Young symmetry type (D − 3, 1, 1). Both ${\tilde{T}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ and ${\tilde{{T}}}_{{\alpha }_1···{\alpha }_{D-3}|\mu \nu }$ are antisymmetrized in α₁···α_{D − 3}, and symmetrized in μν.

The dual Einstein tensor (202) is equivalent to

where the spin-3 dual Riemann tensor ${\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}{\mu }_2{\nu }_2{\mu }_3{\nu }_3}$ is a tensor with Young symmetry type (D − 2, 2, 2), and the spin-3 dual Ricci tensor ${\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}|{\mu }_2{\mu }_3}\equiv {\tilde{R}}_{{\alpha }_1···{\alpha }_{D-2}{\mu }_2{\nu }_2{\mu }_3{\nu }_3}$ is a tensor with Young symmetry type (D − 2, 1, 1), defined by (197).

In the little group SO(D − 2), we may write the following relations

It can easily verify that the spin-3 Einstein equations (201) and (202) are invariant under the twisted self-dual conditions $𝔊={{S}}^{\star }𝔊$ and $𝔗={{S}}^{\star }𝔗$ if we employ the following matrix notations

and the matrix ${S}$ is defined by Equation (38).

Following Equations (116) and (117), for a spin-3 charged particle in D = 4, the spin-3 stress-energy tensors, which are coupled to its field, read

where m is the electric-type spin-3 charge, and $\tilde{m}$ is the magnetic-type spin-3 charge, U_〈μν〉 ≡ u_〈μu_ν〉 denotes the traceless part of u_μu_ν, and Ũ_〈μν〉 ≡ ũ_〈μũ_ν〉 the traceless part of ũ_μũ_ν (the angle brackets denote the traceless part; see e.g., [66, 144] for the same notation). For example, one defines traceless parts of symmetric tensors S_αβ and S_αβρ in 4-dimensional flat spacetime as follows

so the traceless part of u_μu_ν is defined by

Equations (209, 210) can be rewritten as

It can be easily varified that these stress-energy tensors are conserved.

One can write a quantization condition for the spin-3 field in D = 4 similar to the Dirac quantization condition (104) and the spin-2 quantization condition (106) as follows (see [91] for spin-s fields):

where the conserved spin-3 charges are defined by

We now consider the construction of a Dirac string in the spin-3 theory in D = 4. The spin-3 Riemann curvature R_{μ1ν1μ2ν2μ3ν3} can be split into the chargeless and charged terms,

The chargeless term r_{μ1ν1μ2ν2μ3ν3} is of mixed symmetry type (2, 2, 2), and satisfies the cyclic and Bianchi identities. The charged term m_{μ1ν1μ2ν2μ3ν3} is of mixed symmetry type (2, 2, 2), and may be coupled to the spin-3 magnetic-type source

The tensor ${\tilde{M}}_{\alpha \beta |\mu \nu }$, which represents the spin-3 magnetic-type source, is of Young symmetry type (2, 1, 1) ≡ . The notations [ | and | ] separate different antisymmetrized indices from each other, e.g., $4{\partial }_{[{\mu }_1|}{\partial }_{[{\mu }_2|}{S}_{|{\nu }_1]|{\nu }_2]}\equiv 4{\partial }_{[{\mu }_1}{\partial }^{[{\mu }_2}{S}_{{\nu }_1]}{}^{{\nu }_2]}$.

The chargeless term r_{μ1ν1μ2ν2μ3ν3} may be rewritten in terms of covariant derivatives of a symmetric tensor h_μ1μ2μ3:

Let us define $y^{\alpha \beta |}{}_{\mu \rho }={ϵ}^{\alpha \beta \gamma \lambda }{\partial }_{\gamma }{h}_{\lambda \mu \rho }$, where $y^{\alpha \beta |}{}_{\mu \rho }=y^{[\alpha \beta ]}{}_{\mu \rho }=y^{\alpha \beta }{}_{(\mu \rho )}$ is of Young symmetry type (2, 1, 1) tensor (${\partial }_{\alpha }{y}^{\alpha \beta |}{}_{\mu \rho }=0$), the spin-3 Riemann curvature R_{μ1ν1μ2ν2μ3ν3} can be defined by

If we take $Y_{\alpha \beta |\mu \nu }=y_{\alpha \beta |\mu \nu }+{\tilde{M}}_{\alpha \beta |\mu \nu }$ (where Y_μνα = Y_[μν]α), it is obtained

A Dirac string y^μ(τ, θ) can be connected to the spin-3 magnetic-type source ${\tilde{M}}_{\alpha \beta |\mu \nu }$, $y^{\mu }(\tau ,0)={\tilde{w}}^{\mu }(\tau )$ in (210). By analogy with (124), one can write

where the tensor ${\tilde{M}}_{\alpha \beta |\mu \nu }$ defines the spin-3 magnetic-type source as

so the divergence of ${\tilde{M}}_{\alpha \mu |\nu \rho }$ is identical with ${\tilde{T}}_{\mu \nu \rho }$, and the Dirac string of a spin-3 magnetic-type point source is conserved. One can prove the conserved charges associated with a spin-3 electric-type point source (see [91] for complete proof of the spin-s conserved charges with magnetic-type and electric-type point sources).

3.4. Spin-3 Harmonic Condition

The spin-2 harmonic coordinate condition can be generalized to the spin-3 field h_μνλ that allows the propagation of a spin-3 particle in empty space. To have a wave equation for the spin-3 fields in empty space, ${\partial }_{\rho }{\partial }^{\rho }{h}_{\mu \nu \lambda }=0$, it is necessary to eliminate the last two of the spin-3 Fronsdal equation (163):

which is invariant under the gauge transformation (160):

Equation (225) is the De Donder gauge condition for the spin-3 field h_μνλ. To have the De Donder gauge condition, one way is to make the spin-3 field h_μνλ transverse and traceless:

which imply that the gauge parameter ξ_μν is a symmetric, traceless 2-th rank tensor.

The transverse–traceless spin-3 field h_μνλ, which is projected along a four-velocity vector u_λ in the rest-space of a co-moving observer, may be written in terms of its helicity state vectors $h_{\lambda }^{+}$ and $h_{\lambda }^{\times }$, and the polarization tensors $e_{\mu \nu }^{+}$ and $e_{\mu \nu }^{\times }$ in the momentum space $m_{\mu }=(|\overrightarrow{m}|,\overrightarrow{m})$:

where the polarization tensors are

while $x_{\mu }=(0,\widehat{x})$ and y_μ = (0, ŷ) are spatial 4-vectors with $\widehat{x}·\widehat{x}=ŷ·ŷ=1$ and $\widehat{x}·ŷ=0$ with $\widehat{x}·\widehat{m}=$ $ŷ·\widehat{m}=0$ , and form an orthogonal triad $ŷ=\widehat{x}\times \widehat{m}$, where $\widehat{m}=\overrightarrow{m}/\left|\overrightarrow{m}\right|$.

Similarly, the transverse–traceless dual spin-3 field ${\tilde{h}}_{\mu \nu \lambda }$, which is projected along a four-velocity vector ũ_λ in the rest-space of a co-moving observer, may be written in terms of its helicity states ${\tilde{h}}_{\lambda }^{+}$ and ${\tilde{h}}_{\lambda }^{\times }$, and the polarization tensors in D = 4:

Taking a permutation ϵ_μα from Equation (228) according to the first dual formulation definition, one can easily find in the momentum space:

which means that the helicity state vectors of the spin-3 field are respectively rotated to those of its dual field under SO(2) duality rotations in D = 4, and demonstrate the twisted self-dual condition, similar to what were shown the graviton and the dual graviton in section 2.6.

4. Higher-Spin Fields and their Dual Fields

We now consider the general spin-s fields (s ≥ 4) and its dual formulations. The spin-s fields in D-dimensional spacetime can be represented by a symmetric s-th rank tensor h_{μ1μ2···μs} = h_{(μ1μ2···μs)} with the Young diagram:

which is double-traceless for s ≥ 4 [102]:

The action of the free, massless spin-s fields h_{μ1μ2···μs} in arbitrary dimensions (D ≥ 4) reads:

where ${L}\left[h_{{\mu }_1{\mu }_2···{\mu }_s}\right]$ is the Fronsdal Lagrangian [102]:

The Fronsdal Lagrangian (235) is invariant under the gauge transformation [102]

The gauge parameter ξ_{μ2···μs−1} is a symmetric tensor.

The equations of motion for free, massless spin-s fields satisfy the generalized spin-s Einstein equations [91, 102]

where the spin-s Einstein tensor G_{μ1μ2···μs} = G_{(μ1μ2···μs)} is a double-traceless ($G_{{\mu }_1{\mu }_2···{\mu }_s}{\eta }^{{\mu }_1{\mu }_2}{\eta }^{{\mu }_3{\mu }_4}=0$), symmetric tensor.

The spin-s Einstein tensor G_{μ1μ3···μs} can be written using the Fronsdal tensor F_μ1···μs as

where the Fronsdal tensor F_μ1···μs = F_{(μ1···μs)} is a symmetric tensor, and defined by [49, 102]

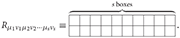
The linearized spin-s Riemann tensor R_{μ1ν1μ2ν2···μsνs} is a (2s)-th rank tensor with Young symmetry $(\stackrel{s}{\overbrace{2,···,2}})$ and the diagram:

The linearized spin-s Ricci tensor,

is a (2s−2)-th rank tensor with Young symmetry type

and obtained by taking covariant derivatives from the Fronsdal tensor F_μ1···μs as follows

Here, the notations [ | and | ] such as 4∂_[ν1|∂_[ν2|S_|μ1]|μ2] imply that covariant derivatives are antisymmetrized on ν₁μ₁ and ν₂μ₂ separately, i.e., $y^{\alpha \beta |}{}_{\mu \rho }=y^{[\alpha \beta ]}{}_{\mu \rho }=y^{\alpha \beta }{}_{(\mu \rho )}$. The equations of motion of a free, massless spin-s field h_{μ1μ2···μs} satisfy R_{μ1ν1μ2ν2···μs−2νs−2|μs−1μs} = 0, which is equivalent to the spin-s Einstein equations (237).

Substituting the Fronsdal definition (239) into the Ricci definition (242) yields [49]

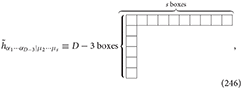
For the spin-s field h_{μ1μ2···μs}, there might be s different dual formulations (also infinite chains of dualities [94, 95]). Considering the fact that spin-s fields are double-traceless (s ≥ 4), it is problematic to dualize on multiple indices. Thus, we consider only the first dual formulation of the spin-s field in D-dimensional spacetime, which is dualized on one index only. For the physical gauge spin-s field, we can write

The dual spin-s field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|{\mu }_2···{\mu }_s}$ is of Young symmetry $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$ having the Young diagram:

and double-traceless for s ≥ 4 [47]:

It has the following properties:

In D = 4, the dual spin-s field is symmetric, ${\tilde{h}}_{{\mu }_1{\mu }_2···{\mu }_s}={\tilde{h}}_{({\mu }_1{\mu }_2···{\mu }_s)}$. The Fronsdal action (234) for the spin-s field h_{μ1μ2···μs} in D = 4 is dual to the Fronsdal action $S=\frac{1}{2}\int d^{4}x{L}\left[{\tilde{h}}_{{\mu }_1···{\mu }_s}\right]$, which is formulated in terms of the dual spin-s field ${\tilde{h}}_{{\mu }_1{\mu }_2···{\mu }_s}$, i.e., $h_{{\mu }_1···{\mu }_s}\to {\tilde{h}}_{{\mu }_1···{\mu }_s}$ in the action (234).

4.1. D > 4: Generalized Dual Fronsdal Fields

The Fronsdal field h_{μ1μ2···μs} is dual to a field dualized on one index. The dual Fronsdal field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|{\mu }_2···{\mu }_s}$ is a double-traceless, tensor with Young symmetry $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$. It is a symmetric tensor in D = 4, whose equations of motion can be described by the Fronsdal Lagrangian (235). In D > 4, the equations of motion of free massless, dual spin-s field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|{\mu }_2···{\mu }_s}$ explicitly reads [47]

which is invariant under the gauge symmetry [47]:

where χ_{α1…αD − 4|β2···βs} = χ_{[α1…αD − 4]β2···βs} = χ_{α1…αD − 4(β2···βs)} is an arbitrary tensor with the mixed symmetry $(D-4,\stackrel{s-1}{\overbrace{1,···,1}})$,

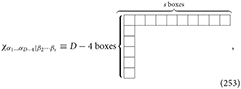
such

The gauge transformations for χ_{α1…αD − 4|β2···βs} are reducible.

The action (251) also has the following gauge symmetry

where χ_{α1…αD − 4|β2···βs} is an arbitrary tensor with the mixed symmetry $(D-4,\stackrel{s-1}{\overbrace{1,···,1}})$, and φ_{α1…αD − 3|β3···βs} = φ_{[α1…αD − 3]μ} is an arbitrary tensor with the mixed symmetry $(D-3,\stackrel{s-2}{\overbrace{1,···,1}})$. The gauge transformations for χ_{α1…αD − 4|β2···βs} and φ_{α1…αD − 3|β3···βs} are reducible.

One may define the spin-s generalized Curtright action of the dual spin-s field ${\tilde{h}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2···{\beta }_s}$ using a field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|{\beta }_2···{\beta }_s}$ as (see Appendix 1 in Supplementary Material):

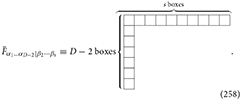
where the “spin-s Curtright” field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|{\beta }_2···{\beta }_s}$ defined as

is a tensor with Young symmetry type $(D-2,\stackrel{s-1}{\overbrace{1,···,1}})$:

The spin-s Curtright field strength tensor ${\bar{F}}_{{\alpha }_1\dots {\alpha }_{D-2}|{\beta }_2···{\beta }_s}$ is transferred as follows

However, it is not gauge invariant under the gauge symmetry (252).

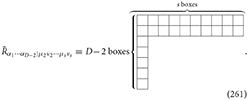
One can define the spin-s dual Riemann tensor by

which has Young symmetry $(D-2,\stackrel{s-1}{\overbrace{2,···,2}})$:

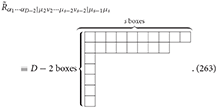
The spin-s dual Ricci tensor is defined by

with Young symmetry $(D-2,\stackrel{s-1}{\overbrace{2,···,2,1,1}})$ and the diagram:

Similarly, there is the spin-s dual Einstein tensor ${\tilde{G}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2\dots {\beta }_s}$ with Young symmetry:

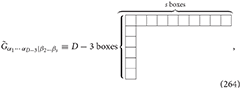
which is defined by

where ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2\dots {\beta }_s}$ is the spin-s dual Fronsdal tensor [47]

The spin-s dual Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2\dots {\beta }_s}$ is of Young symmetry type $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$. In D = 4, the definition (266) recovers Equation (239).

The spin-s dual Ricci tensor (262) can be defined in term of the dual spin-s Fronsdal tensor ${\tilde{F}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2\dots {\beta }_s}$:

Substituting the dual Fronsdal definition (266) into the dual Ricci definition (267) presents

4.2. Spin-s Magnetic-Type Sources

We now introduce the coupling between the spin-s fields h_{μ1μ2···μs} = h_{(μ1μ2···μs)} and spin-s electric-type sources, and then make a generalization to the dual spin-s fields and spin-s magnetic-type sources.

The linearized spin-s Ricci tensor R_{μ1ν1μ2ν2μ3ν3} can be coupled to a traceless (${{T}}_{{\mu }_1{\mu }_2···{\mu }_s}{\eta }^{{\mu }_1{\mu }_2}{\eta }^{{\mu }_3{\mu }_4}=0$), symmetric tensor in D-dimensional spacetime:

The tensor ${{T}}_{{\mu }_1···{\mu }_s}$ is defined by

where T_μ1···μs = T_{(μ1···μs)} is the spin-s electric-type stress-energy tensor.

The spin-s Einstein equations with the spin-s electric-type source read [91]:

The dual spin-s Einstein tensor defined by (265) can be coupled to the spin-s magnetic-type source:

equivalently,

where ${\tilde{{T}}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2···{\beta }_s}$ is a double-traceless $({\tilde{{T}}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2···{\beta }_s}{\eta }^{{\alpha }_1{\alpha }_2}{\eta }^{{\alpha }_3{\alpha }_4}=0={\tilde{{T}}}_{{\alpha }_1···{\alpha }_{D-3}|{\beta }_2\mathrm{...}{\beta }_s}{\eta }^{{\beta }_2{\beta }_3}{\eta }^{{\beta }_4{\beta }_5})$, tensor with Young symmetry type $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$ and defined as

and ${\tilde{T}}_{{\alpha }_1···{\alpha }_{D-3}|{\mu }_2···{\mu }_s}$ is the spin-3 magnetic-type stress-energy, and has Young symmetry type $(D-3,\stackrel{s-1}{\overbrace{1,···,1}})$.

By analogy with the Dirac quantization condition (104), the spin-s quantization condition in D = 4 is [91]

where P_{μ1···μs−1} = mU_{〈μ1···μs−1〉} is the conserved spin-s electric-type charge, and ${\tilde{P}}^{{\mu }_1···{\mu }_{s-1}}=\tilde{m}{Ũ}^{\langle {\mu }_1···{\mu }_{s-1}\rangle }$ is the conserved spin-s magnetic-type charge, m is the electric-type spin-s charge, and $\tilde{m}$ is the magnetic-type spin-s charge, U_{〈μ2···μs〉} ≡ u_〈μ2···u_μs〉 the traceless part of u_μ2···u_μs, and Ũ_{〈μ2···μs〉} ≡ ũ_〈μ2···ũ_μs〉 the traceless part of ũ_μ2···ũ_μs.

The stress-energy electric-type and magnetic-type tensors in D = 4 can be written as

A Dirac string in the 4-D spin-s theory can be constructed as follow. Let us consider the decomposition of the spin-s Riemann curvature R_{μ1ν1···μsνs}, it can be split into the chargeless part and the charged part,

Both r_{μ1ν1···μsνs} and m_{μ1ν1···μsνs} are of mixed symmetry type $(\stackrel{s}{\overbrace{2,···,2}})$. The tensor r_{μ1ν1···μsνs} satisfies the cyclic and Bianchi identities, and can be written in terms of covariant derivatives of a symmetric tensor h_μ1μ2μ3:

The charged part m_{μ1ν1···μsνs} can be defined in terms of the spin-s magnetic-type source:

where the tensor ${\tilde{M}}_{\alpha \beta |{\mu }_2···{\mu }_s}$ is of Young symmetry type $(2,\stackrel{s-1}{\overbrace{1,···,1}})$:

If we define

where the tensor y_{αβ|μ2···μs} is of Young symmetry type $(2,\stackrel{s-1}{\overbrace{1,···,1}})$ tensor,

the spin-s Riemann curvature R_{μ1ν1···μsνs} can be rewritten as

Assuming $Y_{\alpha \beta |{\mu }_2···{\mu }_s}=y_{\alpha \beta |{\mu }_2···{\mu }_s}+{\tilde{M}}_{\alpha \beta |{\mu }_2···{\mu }_s}$, one has

We can now connect a Dirac string y^μ(τ, θ) to the spin-s magnetic-type source ${\tilde{M}}_{\alpha \beta |{\mu }_2···{\mu }_s}$, $y^{\mu }(\tau ,0)={\tilde{w}}^{\mu }(\tau )$ by analogy with (124):

The divergence of ${\tilde{M}}_{\alpha \beta |{\mu }_2···{\mu }_s}$ is equal to ${\tilde{T}}_{{\mu }_1···{\mu }_s}$:

Hence, the Dirac string of a spin-s magnetic-type point source is conserved (see also [91] for spin-s electric-type source).

4.3. Higher-Spin Harmonic Condition

We now introduce a harmonic coordinate condition for the generalized Fronsdal equation (239) that makes the linearized wave equation for spin-s fields by eliminating the last two terms of (239).

To have a wave equation for the spin-s fields in empty space, it is required to have the generalized De Donder gauge condition [103]:

Substituting Equation (288) into (239) leads to the wave equation ${\partial }_{\rho }{\partial }^{\rho }{h}_{{\mu }_1···{\mu }_s}=0$.

It can be seen that Equation (288) is also invariant under the gauge transformation

It was imposed that the spin-s field has the double-traceless condition (233) [102]. To make the De Donder gauge condition (288), one may require that the spin-s field is transverse and traceless (see [145] for proof):

Having the transverse–traceless gauge condition, the gauge parameter ξ_μ2···μs is a symmetric, traceless (s − 1)-th rank tensor. Similar to massless spin-2 fields described in section 2.6, massless, spin-s fields have only two polarization states with the ±s helicity states [146]. However, massive, spin-s fields have 2s+1 polarization states [147, 148].

5. Discussion: Interacting Theories

Consistency of the interacting theory for a free field can traditionally be determined from coupling deformations of the gauge transformations of the free theory. The BRST formalism [149–152] was originally developed to examine whether the deformed gauge transformations can be constructed. Inclusion of auxiliary fields (antifields and ghosts) led to the BRST-antifield formalism [153–157] that allowed us to assess consistency of interactions of the free theory with other theories and itself. This involves studying consistent deformations of the master equation [158, 159], which contains gauge transformation structures, corresponding local reducibilities, as well as stationary surfaces (inc. equations of motion) of each field. The master equation of the free theory is associated with the BRST differential. The coupling-order deformations of the master equation of the interacting theory by means of the BRST differential allow us to evaluate all the requirements for consistency of the interacting theory (see reviews [160–167] ). The action principle of the free theory is the integral of the Lagrangian over the manifold that corresponds to the propagation of perturbations of the free field in the spacetime. Nevertheless, the action of the interacting theory associated with observables, which are invariant under the gauge transformations, may make consistent interactions with themselves or other fields of other free theories. A detail study of consistency of interactions of the free theory of the fields with itself can deduce whether the interacting theory has consistent deformations.

The action principle of a massless, spin-2 field particle is described by the Pauli-Fierz action [100, 111], which corresponds to the linearized Einstein equations in Minkowskian flat spacetime. The Pauli-Fierz action is free of ghost excitations, and its field equations are algebraically consistent. The interacting theory of gravity has only one single massless spin-2 field [168–170], and there are no consistent interactions among multiple interacting massless spin-2 fields [171], i.e., no spin-2 analogy of Yang-Mills theory. However, the action of a single, massless spin-2 field h_μν coupled to a positive-definite dynamical metric is g_μν is not invariant under the h_μν gauge transformation, so it is inconsistent [172]. Similarly, cross-interactions among multiple massless spin-2 fields are inconsistent in a positive-definite metric [171], while consistency is mathematically possible in a negative-definite metric (negative-energy) [171, 173]. In the case of direct coupling to matter, the locality and consistency conditions require that the interacting theory includes all nonlinear terms [168, 169, 174], otherwise the spin-2 field of the linearized theory remains ghost-like in empty flat space [170]. Despite the inconsistency of linear, massless spin-2 interactions, the nonlinear theory of a massive spin-2 field provides ghost-free consistent coupling to matter [175–177]. A spin-2 field coupled to matter or nonlinear self-interaction leads to the general covariance of the interacting theory [169]. Constructing the interacting multi-graviton model and coupling a single spin-2 field to a dynamical metric require a fully non-linear representation of the interacting theory for gravity.

It was proven that the dual formulations of linearized gravity in D = 5, the Curtright Field, does not have consistent interactions involving two derivatives of the fields under local, Poincaré invariance [40]. The dual formulations of linearized gravity in D > 5 do not possess consistent, local deformations [178], so the dual graviton of the linearized theory does not have any self-interaction. However, the dual graviton can be coupled to other theories, such as topological BF theories [132, 179]. To overcome the inconsistency of the linearized dual gravity, one may consider a non-linear theory of the dual graviton, which incorporates a topological (Chern-Simons like) term for the original graviton, which leads to consistent nonlinear deformations, and is manifestly invariant due to a dynamical metric for the dual graviton [134]. In particular, the properties of the Kac-Moody algebra E₁₁ (see section 2.3) are associated with spacetime covariance and supergravity covariant spectra. In the case of D = 11 supergravity, the Kac-Moody algebra ($A_{D-3}^{+++}$ for pure gravity) applies to pure gravity (as well as maximal supergravity), so the dual graviton cannot be coupled to the original Einstein-Hilbert action, and it doubles degrees of freedom. Nevertheless, the dual graviton in the E₁₁ algebra can be coupled with a topological term containing the original metric without any doubling of degrees of freedom [134]. The interacting theory of dual graviton in D ≥ 5 [43] can also be constructed in de Sitter space (dS_n) [180], similar to the nonlinear implementation of gravitational duality with a cosmological constant in dS₄ [181]. Thus, it is necessary to formulate a nonlinear representation of dual gravity (see [134, 182] for nonlinear dual graviton), which is dual to nonlinear Einstein gravity, containing both the original and dual metrics, and is fully gauge covariant.

It has been shown that a massless spin-3 (also s > 3) particle described by a linear gauge field cannot have a self-interaction in D = 4 [183, 184]. Although first-order deformations of spin-3 fields are possible [183], self-interactions encounter some difficulties: the first-order deformations do not obey the Jacobi identity [185], and the commutator of two gauge transformations cannot be written [184]. Similarly, the commutator between two gauge transformations of a linear spin-s gauge field (>3) cannot be constructed in D = 4, so self-interactions of a spin-s field do not exist in 4-D flat space [184]. Using the BRST-antifield formalism, the first-order deformations of a spin-3 gauge field in D = 4, defined by a non-abelian symmetric rank-3 tensor $h_{\mu \nu \rho }^a\equiv h_{(\mu \nu \rho )}^a$, were built under the assumptions of parity and Poincaré invariance, local and perturbative deformation of the free theory in Minkowski space, which correspond to the cubic vertex of Berends, Burgers, and van Dam [183] involving three derivatives of the fields, but the theory is again inconsistent at second order [186]. In D = 5 Minkowski spacetime, the second-order deformations of spin-3 fields can be obtained, while the first-order deformations involve the generalized de Wit–Freedman connection [187]. In D > 4 flat spacetime, the structure constants given by a completely antisymmetric tensor can make a cubic vertex at second order involving five derivatives of the fields, but the analysis will be complicated due to tedious five-derivative calculations [186]. Hence, the interacting theory of linearized spin-3 particles is problematic in flat space D ≥ 4, and only feasible under some certain assumptions involving 3 derivatives at first order and 5 derivatives at second order in spacetime dimensions higher than 4.

The generalizations of the Coleman–Mandula “no-go” theorem [188] to supersymmetry [189] and higher spin gauge theories [190–192] indicate that the interacting theory of linearized higher spin fields (s > 2) are incompatible in flat spacetime, since their conserved currents are associated with a free theory, which does not permit to have a nontrivial S-matrix [190]. The no-go theorem allows us to have only gauge fields of spin-1 and spin-2 perturbations around a flat background. However, the restrictions imposed by the no-go theorem on higher spin fields (s > 2) can be overcome in the nonlinear theory of spin-s perturbations around the anti de Sitter (AdS_d) spacetime of arbitrary d dimensions [193]. It is argued that the interacting theory of nonlinear, massless bosonic fields of arbitrary spins s > 1 can be formulated in d-dimensional AdS space [194–196]. Nonlinear spin-s fields with a non-vanishing cosmological constant in D = 4 were shown to have consistent interaction in the cubic-order [197, 198], and in the first-order in the Weyl 0-forms [199], and also in all orders [200–203] (the so-called Vasiliev higher-spin theory). Consistent interactions of nonlinear spin-s fields were also formulated in 3-D AdS spacetime [204], in AdS₅ spacetime [205, 206], and in AdS_d space with arbitrary d dimensions [207]. In particular, it was shown that irreducible massless mixed symmetry fields in AdS_d are decomposed into certain reducible massless flat fields in the flat limit [208], which permit to have consistent deformations for generic higher-spin fields in the AdS space. It was demonstrated that all spin-s consistent deformations are explicitly made using Vasiliev's unfolded equations in D = 4, which are expressed in terms of a gauge connection and a (twisted)-adjoint matter field, while the Vasiliev gauge connection is found to be related to the spin-s Fronsdal fields [209]. Therefore, the nonlinear, massless higher spin gauge theories can have consistent interactions around the AdS vacuum solution with the non-zero cosmological constant in the Vasiliev higher-spin theory [210].

It is well known that the compactification of M-theory or supergravity on (d + 1)-dimensional AdS spacetime is dual to conformal field theory (CFT) in d dimensions, which is called the AdS_{d + 1}/CFT_d correspondence or Maldacena duality [211]. This correspondence indicates that the chiral operators of ${N}=4$ Super Yang–Mills theory (CFT observables) in D = 4 correspond to those of Kaluza–Klein Type IIB supergravity on $Ad{S}_5\times S^5$ (where S⁵ is a 5-dimensional compact space) [212, 213]. We know that electric-magnetic duality in the bulk of AdS₄ can relate holographically derived deformations of the boundary CFT₃ [50]. It was also argued that gravity theories in AdS₄ are holographically dual to two CFTs in D = 3 with different parity: the Dirichlet CFT₃ with the graviton source and a dual CFT₃ with a dual graviton source at the non-linear level [52]. The holographic properties of electric-magnetic duality in gravity also provide some insights into non-linear aspects of M-theory (see [51] for review). The “yes-go” Vasiliev higher-spin theory of spin-s perturbations in the AdS background is naturally conjectured in the higher-spin holography [214–216], which gives evidence for duality between Vasiliev's higher-spin fields and the free field theory of N massless scalar fields [217], and holographic dualities between Vasiliev's higher-spin fields and O(N) vector models [215, 216] (the so-called higher spin/vector model duality; see [218, 219] for review). The interacting theory of Vasiliev's higher-spin fields may reveal the hidden origin of AdS_{d + 1}/CFT_d correspondence (see [220–222] for more discussions). Nevertheless, we do not yet have any full nonlinear representation of the spin-s Fronsdal fields.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication. The author presented some mathematical notations and expressions slightly different from the original versions, and provided few new results (e.g., Equations 27 and 28 in section 2.1, a part of section 2.6).

Funding

A part of this work was supported by the EU contract MRTN-CT-2004-005104 Constituents, Fundamental Forces and Symmetries of the Universe at University of Craiova in 2008.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AD acknowledges hospitality from the University of Craiova, where a part of this work was carried out, and thanks C. Hull, P. West, M. Vasiliev, G. Barnich, and M. Henneaux for helpful comments and valuable discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00146/full#supplementary-material

Footnotes

References