1 Introduction

The Standard Model (SM) of particle physics has shown tremendous agreement with the experimental results however there are still some question that can not be answered by SM. For example SM can not explain why there are three generations of fermions and why fermion masses are the way they are. These kind of questions can be answered if one assumes the composite structure of the fermions [1,2,3]. This assumption would require the SM to be a limiting case of a more fundamental theory that may introduce new high energy scales. Although an experimental proof of a fundamental structure of the SM fermions has not yet been found and neither a complete model able to reproduce the fermion spectrum has been proposed, these theories predict the existence of heavy excited particles for each SM fermion state. These new particles can leave traces at the TeV scale that motivates the use the effective field theory approach to study the physics related to the compositeness [4]. These signals can be important because in composite models the exotic particles couple to the SM ones through gauge couplings, originating dimension 5 operators. Like in other models with exotic fermions [5] couplings to SM Higgs may be present. However, these interactions [6, 7] result in weaker effects on the SM observables than the ones introduced through compositeness.

There are already several efforts to study the physics at the composite scale. Most of them concentrated on the production of excited fermions at colliders. For example production of excited states members of multiplets of isospin \(I_W=0, 1/2\) was discussed in  [8, 9]. In [10, 11], bounds on the masses of the excited fermions with \(I_W=0,1/2\) were presented on the basis of experimental searches at LHC. On the phenomenological side, excited fermion contributions to the Z pole observables were calculated in [12] and to the leptonic \(\tau \) decay  [13] for the isospin doublet states. However it has been shown that the higher isospin multiplets up to \(I_W=1,3/2\) are also allowed by the standard model symmetries [14]. This will result in the existence of exotic states such as quarks \(U^+\) of charge \(+5/3e\) and quarks \(D^-\) of charge \(-4/3 e\). Phenomenological studies for these exotic states were presented in  [15,16,17,18]. Experimental studies have been able to put stringent bounds on the excited fermion masses (M) but so far there is no direct experimental evidence of the existence of these type of states. Phenomenological studies and experimental searches typically provide bounds in the parameter space \([\Lambda ,M]\), where, \(\Lambda \) is a composite scale. In the absence of direct detection, indirect effects of excited fermions to the standard model observables can be a very good probe for the study of these states. Recently there have been interesting development in the study of the phenomenology of the effective interactions of excited fermions by computing unitarity bounds [19] in the parameter space \([\Lambda , M]\). Such unitarity bounds have been shown to have a potential impact when compared with the bounds from the direct searches at colliders [19].

In this paper, we study the indirect effects of excited fermions with isospin multiplets \(I_W=1\), to the electro-weak precision observables. Our main objective is to derive bounds on the parameter space \([\Lambda , M]\) from the experimental value of electro-weak precision observable (EWPO) \(\Delta \rho \). The contribution of each excited fermion family depends on the magnitude of the corresponding composite scale related to it. As a first step, we just considered the contribution of excited leptons of the first generation and study its scale dependence. The bounds derived in this work from the experimental value of \(\Delta \rho \) are compared with bounds from current experimental searches at LHC run 2 and with the unitarity bounds discussed, for the same model, in [19]. We have calculated the couplings of the excited fermions (leptons) of the triplet to the excited and ordinary fermions (leptons) using an effective field theory approach which will be presented in Sect. 2. The analytical results for the excited fermion (lepton) contribution to the \(\Delta \rho \) observable will be given in Sect. 3. We will present our numerical analysis in Sect. 4. Our conclusions can be found in Sect. 5.

2 Model set-up

The success of the Standard Model raised the hope of extending the particle spectrum beyond the known three families using weak isospin as was previously done for the case of Baryons and Mesons. It is believed that weak isospin can help us predict hypothetical new fermions without reference to the specific dynamic model of their building blocks (so called preons). Using \(I_W=0, 1/2, 1, 3/2\), one can construct new states of fermions which can interact with the ordinary fermions via electroweak boson (\(B^{\mu },W^{\mu }\)) fields and gluon \(G^{\mu a}\) field. In Table 1, we show all such states which can result from higher isospin lepton multiplets. Since we do not make any hypothesis about any specific model we consider that only the first generation of leptons is associated to the compositeness scale \(\Lambda \), the contribution of the other fermions will depend on their corresponding scales, that in principle do not need to be related to \(\Lambda \). If we assume a common compositeness scale for every generation, like it is assumed customarily in current experimental searches [20,21,22] then one gets similar results (i.e. bounds) for every generation.

Table 1 Lepton multiplets for \(I_W=0,1/2,1,3/2\) , their charge Q, hypercharge Y and the fields through which they couple to ordinary leptons
Full size table

Most of the literature adressing the phenomenology of the excited fermions is based on the assumption that they have spin 1/2 and weak iso-spin \(I_W=1/2\). Here we would like to extend our discussion to the case of higher iso-spin multiplets (\(I_W=1\)) [8, 9, 23]. Since the masses of the excited states are expected to be in the TeV range (i.e. much larger than the masses of the Standard Model fermions) it is customarily assumed that they acquire their mass prior to \(SU(2)\times U(1)\) breaking. Thus both the left-handed and right-handed components of the excited leptons belong to the same weak isospin multiplets (and they have the same quantum numbers). Therefore the corresponding coupling to the gauge bosons will be vector-like. Following the same notation as in [12] the coupling of the excited leptons to the gauge bosons is given by the \(SU(2) \times U(1)\) invariant (and CP conserving), effective Langragian:

$$\begin{aligned} \mathcal{L}_{FF}= & {} - \bar{\Psi }^*\Biggl [ \left( g \frac{\tau ^i}{2} \gamma ^\mu W^i_{\mu } + g' \frac{Y}{2} \gamma ^\mu B_\mu \right) \Biggr .\nonumber \\&+ \Biggl . \left( \frac{g \kappa _2}{2 \Lambda } \frac{\tau ^i}{2} \sigma ^{\mu \nu } \partial _\mu W^i_{\nu } + \frac{g' \kappa _1}{2 \Lambda } \frac{Y}{2} \sigma ^{\mu \nu }\partial _\mu B_\nu \right) \Biggr ] \Psi ^*\nonumber \\ \end{aligned}$$
(1)

where we have denoted with \(\Psi ^*\) the excited multiplet whose particle content is described in Table 1, g and \(g'\) are the gauge coupling constants of SU(2) and U(1) respectively and \(\kappa _1, \kappa _2\) are dimensionless couplings. The constant \(\Lambda \) appearing in the dimension-5 part of the lagrangian in Eq. 1 is the compositeness scale. The assumption that exotic leptons acquire masses above the electro-weak scale, implies to consider similar masses for all members of the exotic multiplet. However, the exotic leptons can mix with the SM Higgs boson [5] giving rise to a small splitting of the masses of the mutiplet members. Also, these couplings will give rise to dimension six operators with contribution to the SM observables [6, 7] smaller than the dimension 5 operators, arising from compositeness, under consideration in the present work.

In terms of the physical gauge fields, this can be written as:

$$\begin{aligned} \mathcal{L}_{FF} = - \!\!\! \sum _{V=\gamma ,Z,W} \bar{F} (A_{VFF} \gamma ^\mu V_\mu + K_{VFF} \sigma ^{\mu \nu } \partial _\mu V_\nu ) F\; . \end{aligned}$$
(2)

where F denotes a generic excited fermion field appearing in the multiplet in table 1. Since we have assumed that the left- and right-handed excited leptons have the same quantum numbers under the standard gauge group, the dimension-four piece in Eq. (2) is taken vector-like. Here we write down explicitly the couplings of the \(I_W=0,1/2,1,3/2\) states of the multiplets in Table 1. The higher multiplets of course include states with exotic charge like doubly charged leptons which were not included in the study in [12] where only the doublet was considered. The couplings \(A_{VFF}\) are given by:

$$\begin{aligned} \begin{array}{ll} A_{\gamma E^{-}E^{-}} = - e , &{}\;\;\;\; A_{\gamma E^{0}E^{0}} = 0 \\ A_{\gamma E^{--}E^{--}} = -2e , &{}\;\;\;\; A_{ZE^{0}E^{0}} = \displaystyle \frac{e}{ s_W c_W} \\ A_{ZE^{-}E^{-}} = \displaystyle \frac{ e s_W }{ c_W}, &{}\;\;\;\; A_{ZE^{--}E^{--}} = \displaystyle \frac{ -e (1- 2 s^2_W) }{s_W c_W} \\ A_{WE^{0}E^{-}} = \displaystyle \frac{ e}{ s_W}, &{}\;\;\;\; A_{WE^{-}E^{--}} = \displaystyle \frac{e }{s_W}\\ A_{W E^{0}E^{--}} = 0 &{} \end{array} \end{aligned}$$
(3)

where \(c_W=\cos \theta _W\) and \(s_W=\sin \theta _W\), \(\theta _W\) being the Weinberg angle, while the couplings \(K_{VFF}\) are given by

$$\begin{aligned} \begin{array}{ll} K_{\gamma E^{0}E^{0}} = - \frac{\displaystyle e}{\displaystyle 2 \Lambda } (\kappa _2 - \kappa _1) ,&{}\; K_{\gamma E^{-}E^{-}} = \frac{\displaystyle e}{\displaystyle 2 \Lambda } \kappa _1 \\ K_{\gamma E^{--}E^{--}} = - \frac{\displaystyle e}{\displaystyle 2 \Lambda } (\kappa _2 + \kappa _1),&{}\; K_{WE^{0}E^{-}} = \frac{\displaystyle e \kappa _2}{\displaystyle 2 \Lambda s_W} \\ K_{WE^{-}E^{--}}= \frac{\displaystyle e}{\displaystyle 2 \Lambda s_W} ,&{}\; K_{Z E^{-}E^{-}} = \frac{\displaystyle e \kappa _1 s_W}{\displaystyle 2 \Lambda c_W} \\ K_{Z E^{0}E^{0}} = \frac{\displaystyle e ( \kappa _1 s^2_W + \kappa _2 c^2_W)}{\displaystyle 2 \Lambda c_W s_W} ,&{}\\ K_{Z E^{--}E^{--}} = \frac{\displaystyle e ( \kappa _1 s^2_W - \kappa _2 c^2_W)}{\displaystyle 2 \Lambda c_W s_W} \end{array} \end{aligned}$$
(4)

The \(SU(2)\times U(1)\) invariant and CP conserving dimension-five effective Lagrangian describing the coupling of the excited fermions to the usual fermions, which ensures the conservation of the electro-magnetic current is of the magnetic-type and can be written as [4]

$$\begin{aligned} \mathcal{L}_{Ff}= & {} - \frac{1}{2 \Lambda } {\bar{\Psi }^*} \sigma ^{\mu \nu } \left( g f_2 \frac{\tau ^i}{2} W^i_{\mu \nu } + g' f_1 \frac{Y}{2} B_{\mu \nu }\right) \psi _L \nonumber \\&+ \; \text {h. c.} , \end{aligned}$$
(5)

where \(f_2\) and \(f_1\) are dimensionless factors of order unity associated to the SU(2) and U(1) coupling constants, and \(\sigma _{\mu \nu } = (i/2)[\gamma _\mu , \gamma _\nu ]\). At tree-level they can be expressed in terms of the electric charge, e, and the Weinberg angle, \(\theta _W\), as \(g=e/\sin \theta _W\) and \(g'=e/\cos \theta _W\). It is customary to assume a pure left-handed structure for the transition couplings in order to comply with the strong bounds which are available from the measurement of the anomalous magnetic moment of leptons [24,25,26]. In terms of the physical fields, the Lagrangian (5) becomes

$$\begin{aligned} \mathcal{L}_{Ff}= & {} - \sum _{V=\gamma ,Z,W} C_{VFf} \bar{F} \sigma ^{\mu \nu } (1 - \gamma _5) f \partial _\mu V_\nu \nonumber \\&- i \sum _{V=\gamma ,Z} D_{VFf} \bar{F} \sigma ^{\mu \nu } (1 - \gamma _5) f W_\mu V_\nu + \text {h.c.}, \end{aligned}$$
(6)

where F are the excited fermion states, f the ordinary (SM) fermions and \(V=\gamma , Z,W\) are the physical vector boson fields. The non-abelian structure of (5) introduces a quartic contact interaction, such as the second term in the r.h.s. of Eq. (6). In this equation, we have omitted terms containing two W bosons, which do not play any role in our calculations. Using (5) and (6), we have calculated, for the case of \(I_W=1\) lepton multiplets, the couplings \(C_{VFf}\) and \(D_{VFF}\) which are given in (7) and (8). For the case of \(I_W=0,1/2\) multiplets we refer the reader to [12].

$$\begin{aligned} \begin{array}{ll} C_{\gamma E^{-} e} = - \frac{\displaystyle e }{\displaystyle \Lambda } f_{1}, &{}\;\;\;\; C_{Z E^{-} e} = - \frac{\displaystyle e c_W}{\displaystyle \Lambda s_W} f_{1}\ \\ C_{W E^{0} e} = \frac{\displaystyle e }{\displaystyle \Lambda s_W} f_1 , &{}\;\;\;\; C_{W E^{--} e} = \frac{\displaystyle e }{\displaystyle \Lambda s_W} f_1\ \\ &{} \end{array} \end{aligned}$$
(7)

and the quartic interaction coupling constant, \(D_{VFf}\), is given by

$$\begin{aligned} \begin{array}{l} D_{\gamma E^{0} e} = - D_{\gamma E^{--} e}= \frac{\displaystyle -e^2 }{\displaystyle 4 \Lambda s_W } f_1\ \\ D_{Z E^{0} e} = - D_{Z E^{--} e} = \frac{\displaystyle e^2 c_W}{\displaystyle 4 \Lambda s^2_W } f_1\ \\ D_{W E^{-} e} = \frac{\displaystyle - e^2 }{\displaystyle 4 \Lambda s^2_W } f_1\ \end{array} \end{aligned}$$
(8)

3 Excited lepton contribution to \(\Delta \rho \)

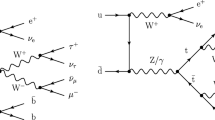
In this section we concentrate on the computation of the contribution of the excited leptons to \(\Delta \rho \). This contribution can be considered as representative of the fermion contributions of the first family. Feynman diagrams for Z and W boson self energies involving ordinary leptons and excited leptons in the loop are shown in Fig. 1.

Fig. 1
figure 1

W and Z boson self energy Feynman diagrams containing excited lepton in the loop

Full size image

The universal corrections to the electroweak precision observable \(\Delta \rho \) can be calculated by the formula

$$\begin{aligned} \Delta \rho ^{\text {ex}}_{\text {univ}}(s)= & {} -\frac{\displaystyle \Sigma ^{ZZ}_{\text {ex}}(s)-\Sigma ^{ZZ}_{\text {ex}}(z)}{\displaystyle s-z} +\frac{\displaystyle \Sigma ^{ZZ}_{\text {ex}}(z)}{\displaystyle z}\nonumber \\&-\frac{\displaystyle \Sigma ^{WW}_{\text {ex}}(0)}{\displaystyle w } + 2\frac{\displaystyle s_W}{\displaystyle c_W} \frac{\displaystyle \Sigma ^{\gamma Z}_{\text {ex}}(0)}{\displaystyle z} \end{aligned}$$
(9)

where \(\Sigma ^{V_1V_2}(s)\) represents the transverse part of the vacuum polarization amplitude \(\Pi ^{V_1V_2}_{\mu \nu }(s)\) between the vector boson \(V_1 - V_2\) calculated at scale s, \(w(z) = M^2_{W(Z)}\).

The analytical results for the contributions of the excited lepton doublets to the transverse part of the vector boson self energies were calculated in [12] using dimensional regularization techniques. In this work, we have calculated the contributions to the vector boson self energies coming from the excited lepton triplet states using the mathematica package FeynCalc [27, 28] and cross-checked our results with direct analytical calculations. The generic formulae for the transverse part of the vector boson self energies for the excited lepton triplet are the same as for the case of excited lepton doublets. The transverse part of the vector boson self energy diagram with ordinary lepton and excited lepton in the loop is given by (see [12] for details)

$$\begin{aligned} \Sigma ^{V_1 V_2}_{Ff}= & {} \frac{\displaystyle 1}{\displaystyle 12 \pi ^2} C_{V_1Ff} C_{V_2Ff} \; \Biggl \{ 6 q^2 \Lambda ^2 + q^4 \log \frac{\displaystyle \Lambda ^2}{\displaystyle M^2}- 2 q^2 M^2\nonumber \\&-\frac{\displaystyle q^4}{\displaystyle 3}+ M^2(2M^2-q^2) + (M^2 - q^2)(2M^2 + q^2)\nonumber \\&\times \left[ -2 + \left( 1-\frac{\displaystyle M^2}{\displaystyle q^2}\right) \log \left( 1-\frac{\displaystyle q^2}{\displaystyle M^2} \right) \right] \Biggr \} \end{aligned}$$
(10)

where \(V_{1(2)}\) represent the initial (final) vector boson, q is external momentum and M is the mass of excited leptons in the loop. The transverse part of the self energy diagrams that contains two degenerate excited leptons in the loop can be written as

$$\begin{aligned} \Sigma ^{V_1 V_2}_{FF}= & {} \frac{\displaystyle 1}{\displaystyle 24\pi ^2} \; \frac{\displaystyle q^2}{\displaystyle M^2} \Biggl \{6 K_{V_1FF} K_{V_2FF} M^2 \Lambda ^2 \nonumber \\&+ \Bigl [ 2 A_{V_1FF} A_{V_2FF} + 6 \left( A_{V_1FF} K_{V_2FF} + A_{V_2FF} K_{V_1FF}\right) M\nonumber \\&+ 3 K_{V_1FF} K_{V_2FF} \left( \frac{\displaystyle q^2}{\displaystyle 3} + 2 M^2\right) \Bigr ] M^2 \log \frac{\displaystyle \Lambda ^2}{\displaystyle M^2}\nonumber \\&+ 4 A_{V_1FF} A_{V_2FF}M^2 \left( \frac{\displaystyle 1}{\displaystyle 3}+ \frac{\displaystyle 2 M^2}{\displaystyle q^2}\right) \nonumber \\&+ 6 (A_{V_1FF} K_{V_2FF} + A_{V_2FF} K_{V_1FF}) M^3 \nonumber \\&+ K_{V_1FF} K_{V_2FF} M^2 \left( \frac{\displaystyle 5 q^2}{\displaystyle 3} + 4 M^2\right) \nonumber \\&- 2 \frac{\displaystyle (4 M^2 -q^2)^{1/2}}{\displaystyle q} \arctan \left[ \frac{\displaystyle q}{\displaystyle (4 M^2 - q^2)^{1/2}}\right] \nonumber \\&\times \,\Bigg [ 2 A_{V_1FF} A_{V_2FF}M^2 \left( 1+ \frac{\displaystyle 2 M^2}{\displaystyle q^2}\right) \nonumber \\&+ 6 (A_{V_1FF} K_{V_2FF} + A_{V_2FF} K_{V_1FF}) M^3\nonumber \\&+ K_{V_1FF} K_{V_2FF} M^2 \left( q^2+ 8 M^2\right) \biggr ] \Biggr \} \end{aligned}$$
(11)

In the large-M limit, for \(R_Q \equiv q^2/M^2 \ll 1\), we get

$$\begin{aligned} \Sigma ^{V_1V_2}_{\text {ex}}= & {} \Sigma ^{V_1V_2}_{\text {Ff}}+ \Sigma ^{V_1V_2}_{\text {FF}} \nonumber \\= & {} \frac{\displaystyle M^2}{\displaystyle 12\pi ^2} R_Q \Biggl \{3\Lambda ^2 ( 2C_{V_1Ff} C_{V_2Ff}+K_{V_1FF} K_{V_2FF}) \nonumber \\&-A_{V_1FF} A_{V_2FF} -3 (A_{V_1FF} K_{V_2FF} + A_{V_2FF} K_{V_1FF}) M \nonumber \\&- 6 K_{V_1FF} K_{V_2FF}M^2 - 3 C_{V_1Ff} C_{V_2Ff}M^2\nonumber \\&+ \left[ A_{V_1FF} A_{V_2FF} + 3 (A_{V_1FF} K_{V_2FF} + A_{V_2FF} K_{V_1FF}) M\right. \nonumber \\&\left. + 3 K_{V_1FF} K_{V_2FF} M^2\right] \log \frac{\displaystyle \Lambda ^2}{\displaystyle M^2}\Biggr \} \end{aligned}$$
(12)

The universal corrections to \(\Delta \rho \) coming from the weak iso-spin doublet in the large-M limit are then given by

$$\begin{aligned} \Delta \rho (M_{Z}^{2})= & {} \frac{\alpha R_{z}}{720\pi }\frac{c_W^4+s_W^4}{c_W^2s_W^2} \biggl [-20-60 k \sqrt{R_L}-50f^{2}R_{L} \biggr . \nonumber \\&\biggl .-15k^{2}R_{L}+30f^{2}R_{L}\mathrm {log}{} { R_{L}}+15{ k}^{2}{} { R_{L}} \mathrm {log} { R_{L}}\biggr ] \end{aligned}$$
(13)

where \(R_Z=M_Z^2/M^2\), \(R_L=M^2/\Lambda ^2\) and for simplicity we have assumed that \(f_1 = f_2=f\) and \(k_1=k_2=k\). The universal corrections resulting from weak iso-spin triplet calculated using the couplings given in (3), (4) and (7), are given below,

$$\begin{aligned} \Delta \rho (M_{Z}^{2})= & {} -\frac{\alpha }{72\pi } R_{z}\biggl [\biggl (40f^{2}R_{L}+24f^{2}R_{L}\ln R_{L}\nonumber \\&+48R_{Z}R_{L}-2k^{2}R_{L}+6R_{L}\ln R_{L}\biggr )\cot ^{2}\theta _{W}\nonumber \\&-(3k^{2}R_{L}+9R_{L}\ln R_{L})\tan ^{2}\theta _{W}\biggr ]. \end{aligned}$$
(14)

The results presented in (13) and (14) were obtained with the assumption that the masses of the excited leptons are degenerate. However, mass splitting between the excited leptons can have considerable impact on the predictions for \(\Delta \rho \). For example, the W boson self energy \(\Sigma _{ex}^{WW}(0)=0\) if the excited leptons in the loop have equal masses. However there will be non-zero contribution from W boson self energy \(\Sigma _{ex}^{WW}(0)\) to \(\Delta \rho \) if the masses of the excited leptons in the loop are different. These contributions are given by the formula

$$\begin{aligned} \Delta \rho= & {} -\frac{G_{\mu }}{2\sqrt{2}\pi ^{2}} \biggl \{F(M_{E^{0}}^{2},M_{E^{-}}^{2})+F(M_{E^{-}}^{2},M_{E^{--}}^{2}) \biggr .\nonumber \\&-2(M_{E^{0}}-M_{E^{-}})^{2}\biggl [\ln \frac{\Lambda ^{2}}{M_{E^{0}}M_{E^{-}}}\nonumber \\&-\frac{M_{E^{0}}^{2}+M_{E^{-}}^{2}}{2(M_{E^{0}}^{2}-M_{E^{-}}^{2})}\ln \frac{ M_{E^{0}}^{2}}{M_{E^{-}}^{2}}\biggr ] \nonumber \\&-2(M_{E^{-}}-M_{E^{--}})^{2}\biggl [\ln \frac{\Lambda ^{2}}{M_{E^{-}}M_{E^{--}}}\nonumber \\&-\frac{M_{E^{-}}^{2}+M_{E^{--}}^{2}}{2(M_{E^{-}}^{2}-M_{E^{--}}^{2})}\ln \frac{ M_{E^{-}}^{2}}{M_{E^{--}}^{2}}\biggr ]\biggr \} \end{aligned}$$
(15)

Where \(G_{\mu }\) is the usual Fermi constant. The function \(F_{0}(m_{1}^{2},m_{2}^{2})\) which is proportional to the mass splitting is defined as

$$\begin{aligned} F_{0}(m_{1}^{2},m_{2}^{2})=m_{1}^{2}+m_{2}^{2}-\frac{2m_{1}^{2}m_{2}^{2}}{m_{1}^{2}-m_{2}^{2}}\ln \frac{m_{1}^{2}}{m_{2}^{2}} \end{aligned}$$
(16)

4 Numerical results

The new physics effects to the electroweak precision observables are usually described in terms of a set of three independent parameters called oblique parameters S, T and U [29, 30]. The \(\Delta \rho \) is related to the oblique parameter T via the relation

$$\begin{aligned} \Delta \rho = \hat{\alpha }(M_Z) T \end{aligned}$$
(17)

where electromagnetic fine structure constant \(\hat{\alpha }(M_Z)^{-1}=127.950\pm 0.017\) [31]. The current value for \(T=0.03\pm 0.12\) [31] can be used to put bounds on the value of \(\Delta \rho \) given by

$$\begin{aligned} -0.0007 \le \Delta \rho \le 0.0012 \end{aligned}$$
(18)

Fixing \(U=0\) results in better precision on T given by \(T= 0.05\pm 0.06\) which in turn yield more stringent limits for \(\Delta \rho \)

$$\begin{aligned} -0.000078 \le \Delta \rho \le 0.00086 \end{aligned}$$
(19)

Using the formulae given in (13) and (14), we can estimate the contributions of the excited leptons to the \(\Delta \rho \). In Fig. 2 we show our numerical results for excited lepton doublet and triplet contributions to \(\Delta \rho \) as a function of the excited lepton mass M. Here we fix the cut-off scale \(\Lambda = 2\) TeV and set \(f=k=1\). As one can see the doublet (solid blue line) and triplet (solid orange line) contributions in the degenerate case are well within the experimental bounds on \(\Delta \rho \) given in (19) except for a small range of excited lepton mass \(M<200\) GeV for doublet contribution and \(M<500\) GeV for triplet contribution which however is already excluded by the experimental searches.

Fig. 2
figure 2

Excited lepton doublet (blue line) and triplet (orange line) contributions to \(\Delta \rho \) as a function of excited lepton mass M. Dashed black line shows the experimental lower bound on \(\Delta \rho \)

Full size image

We assume that main contribution to the excited fermion masses arise at scale above EWSB and therefore we assume that they are of similar magnitude with small differences arising from SU(2) breaking contributions like couplings to exotic Higgs bosons. As already discussed, this computation is very sensitive to even small mass splittings of the SU(2) multiplets and can result in large contributions to \(\Delta \rho \) in the form of W boson self energy as shown in (15). Therefore we introduce mass splitting between the excited Fermions and study its impact on the \(\Delta \rho \) for the doublet and triplet contributions. Here we define \(M_{E^{0}}=M-\Delta M\), \(M_{E^{-}}=M\), and \(M_{E^{--}}=M+ \Delta M\).

Extending our analysis for the case of non degenerate masses, we show the bounds from \(\Delta \rho \) in \((M,\Lambda )\) plane using (19) in Fig. 3. Here again we fix \(f=k=1\). Our effective lagrangian approach is not valid on the region with \(M > \Lambda \), shaded in dark grey. We find that constrained areas by \(\Delta \rho \) above the line \(\Lambda =M\) can be found for mass splittings larger than about 10 GeV, excluded areas with \(\Delta M= 15\) GeV (Dot-dashed black line) and \(\Delta M= 25\) GeV (Dot-dashed brown line) are shown. Area below the lower dot-dashed lines is excluded due to the lower bound on \(\Delta \rho \) while the area above the upper dot-dashed lines is excluded by upper bound on \(\Delta \rho \). We have significant doublet contributions for \(\Delta M= 15\) GeV (black dot-dash line) which can result in exclusion of small area in the lower right corner of the \((M,\Lambda )\) plane due to the lower experimental bound on \(\Delta \rho \). Increasing the \(\Delta M\) to 25 GeV not only results in the exclusion of larger part of the \((M,\Lambda )\) plane in the lower right corner of the plot but some area in the upper left corner also gets excluded, as indicated by the dot-dashed brown line, due to upper experimental limit on \(\Delta \rho \). We also show the experimental findings here depicting the exclusion regions in the \((M,\Lambda )\) plane with 95\(\%\) C.L. [21, 22]. The dashed blue line corresponds to the recent CMS search in \(\ell \ell \gamma \) channel with integrated luminosity of 35.9 \(\mathrm {fb^{-1}}\) and orange line corresponds to the search for excited lepton decaying to two electrons or two muon and two jets via contact interaction with a total integrated luminosity of 77.4 \(\mathrm {fb^{-1}}\). The perturbative unitarity bounds for a composite fermion model were studied in [19]. These bounds are depicted using purple line with decreasing thickness corresponding to 100\(\%\), 95\(\%\) and 50\(\%\) event fractions respectively that satisfy unitarity bounds. The unitarity bound discussed in [19] in connection with the single production of excited fermions in quark-quark scattering provides a relation between \(\sqrt{\hat{s}}\), the energy in the parton-parton center of mass frame and the parameters \(\Lambda , M\):

$$\begin{aligned} \frac{g_*^4 \, \hat{s} \, (2\hat{s}+M^{2})}{288 \pi ^2 \Lambda ^4} \left( 1-\frac{M^{2}}{\hat{s}} \right) ^{2} \le 1 \, . \end{aligned}$$
(20)

As discussed in [19] this constraint is implemented in the simulation workflow of the LHC proton-proton collisions imposing it event by event. Accepting only the events that satisfy the constraint in Eq. (20) would give the unitarity bound with 100% of the events satisfying the bound (thicker purple curve). Points in the parameter space below such 100% curve violate unitarity signaling a breakdown of the EFT expansion we are using which could be corrected by adding higher dimension operators in the EFT expansion (higher powers of \(\sqrt{s}/\Lambda \)). Providing curves of the unitairty bounds with 95% and 50% of the events satisfying the unitarity bound respectively is a way of taking into account the fact that we do not know the ultraviolet completion of the model. For instance allowing 50% of the events to violate unitarity corresponds to assigning a relative correction to the cross section \(\delta \sigma /\sigma \le 0.5\) from higher order terms [19]. The shaded areas below the 100%, 95% and 50% solid lines (purple) are excluded due to the unitarity bounds while the shaded areas below the dashed lines (blue and orange) are excluded from and direct searches at the LHC.

Fig. 3
figure 3

Bound from \(\Delta \rho \) in the parameter space \((M, \Lambda )\) for the case of excited lepton doublet with \(\Delta M= 15\) GeV, dot-dashed lines (black) and \(\Delta M= 25\) GeV, dot-dashed lines (brown). The excluded area with \(M>\Lambda \) is shown in dark grey. Solid (purple) lines indicate the unitarity bound [19] with respectively 100%, 95% and 50% of the events while the dashed (blue and orange) lines are the exclusion limits from LHC run 2 for charged leptons searches with two different final states are also shown for comparison [21, 22]

Full size image
Fig. 4
figure 4

Bound from \(\Delta \rho \) in the parameter space \((M, \Lambda )\) for the case of excited lepton triplet with \(\Delta M= 10\) GeV, dot-dashed lines (black) and \(\Delta M= 15\) GeV, dot-dashed lines (brown). The excluded area with \(M>\Lambda \) is shown in dark grey. The other curves and shadings are as in Fig. 3

Full size image

In Fig 4, we show the bounds from \(\Delta \rho \) in \((M, \Lambda )\) plane using (19) for the case of excited lepton triplet. In this case the space above the excluded area with \(M>\Lambda \) (shaded in dark grey) is constrained by \(\Delta \rho \) for mass splittings larger than 5 GeV. Here the space above the bounds are more stringent compared to unitarity bounds even for \(\Delta M= 10\) GeV as indicated by the dot-dash black line. Increasing the mass splitting between the triplets to \(\Delta M= 15\) GeV result in the exclusion of larger area in the lower right region (area below the lower brown line) as well as the upper left corner of the plot (area above the upper dot-dash brown line).

5 Conclusions

The phenomenology of the effective interactions of a composite scenario of the standard model fermions based on extended isospin multiplets (\(I_W=1, 3/2\)) has recently been revived with several studies of the production at LHC of the corresponding states with exotic charge such as doubly charged leptons and quarks of charge \(Q=5/3 e\). On the other end both the ATLAS and CMS Collaborations have been testing this model at increasingly higher energies and luminosities extending the corresponding bounds in the parameter space \([\Lambda ,M]\) with new analyses. Plans are laid out to further these studies at the high luminosity (HL) option of the LHC collider.

In addition to direct searches for the excited fermions at the LHC also perturbative unitarity bounds proved very effective in constraining the composite fermion models [19]. In this paper, however, we have adopted yet another approach in order to constrain the excited fermion parameter space. We analyzed the effects of excited leptons to the electroweak precision observables (EWPO) in particular the \(\Delta \rho \) parameter. As a first step, we calculated the couplings of the \(I_W=1\) multiplet excited leptons to the ordinary leptons and gauge bosons and the direct coupling of the excited leptons to the gauge bosons. In the second step, we used these couplings to calculate the one-loop contributions to the W, Z and \(\gamma \) self-energies for the case of the lepton triplet. These self-energy contributions were then used to estimate the value of \(\Delta \rho \). For the case of mass degenerate excited leptons, their contributions to \(\Delta \rho \) turned out to be very small. However, mass splitting between the excited leptons can result in the large contributions to the \(\Delta \rho \) coming from the W boson self energy diagram. These contributions are directly proportional to the mass splitting and can results in the exclusion of significant regions in the [\(\Lambda ,M\)] plane compared to the present experimental bounds and those coming from perturbative unitarity. We believe that this study will prove helpful for the present and future experimental searches on these models.