1 Introduction

The Standard Model (SM) of particle physics predicts the existence of three generations of fermions and has been confirmed by experiments. Why are there only three generations? So far, we donot have a good understanding and so it is worth exploring the possible experimental consequences of additional fermions. There are powerful constraints on the possibility of an additional SM-like chiral fermions from the Large Hadron Collider (LHC) data [1]. One possibility is an additional vector-like generation, where a SM-like generation is paired with one of opposite chirality. They can acquire masses independently of their Yukawa couplings to the Higgs boson and thus they are much less constrained.

In this work, we consider \(SU(2)_{L}\) singlet charged vector-like leptons (VLL) model. The VLL (\(\tau ^{'\pm }\)) are hypothetical new fermions that transform in non-chiral representations of the unbroken SM gauge group, they are among the simplest SM extensions near the electroweak scale. The VLL and their associated SM leptons have identical lepton numbers and the VLL mass is the only free parameter [2]. Compared with the electron and muon, the relative weakness of lepton flavor-violation constraints involving the \(\tau \) lepton is that the VLL coupling to SM leptons is mostly with the third family, and therefore the \(\tau ^{'}\) decay mostly to final states involving the \(\tau \) lepton [3]. In Ref. [4], the authors have studied the VLL decays mostly to muons and derived some generally applicable limits on various VLL pair production and decay processes. They pointed out that BR(\(\tau ^{'}\rightarrow Z \mu \)) must be less than 92%, 76% and 75% for the singlet VLL \(m_{\tau ^{'}} =125, 150, 200\ \hbox {GeV}\), respectively.

An earlier study [5] excluded the \(\tau ^{'}\) mass up to 101.2 GeV from the non-discovery by the CERN large electron-positron (LEP) collider experiments. Recently, the ATLAS Collaboration has performed a search for the heavy charged leptons decaying to a Z boson and an electron or a muon, and excluded the mass range 129–176 GeV (114–168 GeV) for electron-only (muon-only) mixing, except for the interval 144–163 GeV (153–160 GeV) [6]. The CMS Collaboration has executed a search for the VLLs in multilepton final states, and excluded the mass range of 120–790 GeV for an SU(2) mass degenerate VLL doublet with couplings to the third generation SM leptons [2]. In Ref. [3], the authors studied the possibilities for discovering or excluding VLLs at the LHC of \(\sqrt{s}=8\ \hbox {TeV}\) and \(\sqrt{s}=13\ \hbox {TeV}\) in different multilepton searches. They points out that it is possible to set a 95% Conference Level (CL) exclusion in \(\ge 3 e/\mu + 1\tau _{h}\) channel with 350 fb\(^{-1}\) luminosity for 130 GeV \(< M_{\tau ^{'}}<\) 150 GeV of the singlet VLL model at the LHC of \(\sqrt{s}=13\ \hbox {TeV}\). For the modified singlet VLL model assuming BR(\(\tau ^{'}\rightarrow Z \tau \))=1, it is possible to set a 95% CL exclusion in 5-lepton signal channel with 100 fb\(^{-1}\) luminosity for \(M_{\tau ^{'}}\) up to 250 GeV at the LHC of \(\sqrt{s}=13\ \hbox {TeV}\). With a very high integrated luminosity of 1000 fb\(^{-1}\), it may be possible to set a 95% CL exclusion for a narrow range of 140 GeV \(< M_{\tau ^{'}}<\) 165 GeV using multilepton events at the LHC of \(\sqrt{s}=13\ \hbox {TeV}\). In Ref. [7], the authors pointed out that weak-isosinglet VLLs present a much more difficult challenge, with some reach for exclusion, but not for discovery at future proton-proton colliders.

Compared to the proton colliders, the lepton colliders could provide much cleaner environment to detect the VLL. At the electron-positron collider, we could search for \(\tau ^\prime \) by the s channel \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\). Besides, the incident beams can be polarized, which will to improve strongly the potential of searches for new particles and the identification of their dynamics. Some lepton collider design plans have been put forward, such as the Circular Electron Positron Collider (CEPC) [8], the Future Circular Collider in electron-positron mode (FCC-ee) [9], the International Linear Collider (ILC) [10, 11] and the Compact Linear Collider (CLIC) [12, 13]. In this work, we will focus on the ILC and CLIC since they have higher energy.

The paper is organized as follows: In Sect. 2, we give a brief review of the singlet VLL model. In Sect. 3, we present the details of event generation including the calculations of the polarized cross section, the left-right asymmetry and the detailed signal and background analysis. In Sect. 4, we display the numerical results including the cut scheme of our simulation and the excluding and discovering capability for the VLL in pure leptonic channel and fully hadronic channel at different colliders. Finally, we give a summary in Sect. 5.

2 A brief review of the model

In this work, we consider the detection ability of the \(e^+ e^-\) colliders for VLLs in the singlet model (referred to as the singlet VLL model). The singlet VLL model contains the SM fields and interactions, \(SU(2)_L\) singlet charged VLL \(\tau ^{\prime -}\) and its antiparticle \(\tau ^{\prime +}\). We transform \(SU(3)_C \times SU(2)_L \times U(1)_Y\) leptons \(\tau ^{\prime \pm }\) as a 2-component left-handed fermions [14, 15]

$$\begin{aligned} \tau ^{\prime }+\bar{\tau }^{\prime }=(\mathbf {1}, \mathbf {1},-1)+(\mathbf {1}, \mathbf {1},1) \end{aligned}$$
(1)

In the singlet VLL model, the fermion mass terms and \(\tau ^{\prime }\) mixing with the SM lepton can be obtained from the Lagrangian equation written in the form of a 2-component fermion [3]

$$\begin{aligned} -{\mathcal {L}}=m_{\tau ^{\prime }} \tau ^{\prime } \bar{\tau }^{\prime } +\epsilon H L \bar{\tau }^{\prime }+y_{\tau } H L \bar{\tau }+\mathrm{c.c.} \end{aligned}$$
(2)

where \(L = (\nu _\tau , \tau )\) is the SM third family lepton doublet based on the gauge eigenstate, \(\bar{\tau }\) is the antiparticle of \(\tau \) lepton, H is the SM Higgs complex doublet scalar field, \(y_\tau \) is the \(\tau \) Yukawa coupling in the SM and \(\epsilon \) is a small Yukawa couplings to the Higgs field providing the mixing mass with \(\tau \) lepton. The relevant particle fields and their SM quantum numbers are listed in Table 1.

Table 1 The relevant particle fields and their SM quantum numbers in Eq. (2)
Full size table

The charged fermion mass matrix based on the gauge eigenstate is

$$\begin{aligned} -{\mathcal {L}}=\left( \begin{array}{ll} \tau&\tau ^{\prime } \end{array}\right) {\mathcal {M}}\left( \begin{array}{l} \bar{\tau } \\ \bar{\tau }^{\prime } \end{array}\right) +\mathrm{c.c.} \end{aligned}$$
(3)

where \({\mathcal {M}}\) is a single weak-isosinglet bare fermion mass parameter and responsible for the VLL mass, with

$$\begin{aligned} {\mathcal {M}}=\left( \begin{array}{cc} y_{\tau } v &{} 0 \\ \epsilon v &{} M \end{array}\right) \end{aligned}$$
(4)

where \(v = \langle H \rangle \approx 174\ \hbox {GeV}\) is the SM Higgs vacuum expectation value. The tree-level mass eigenvalues, obtained from the square roots of the eigenvalues of \({\mathcal {M}}^{\dagger }{\mathcal {M}}\) after expanding for \(y_\tau \) \(v\), \(\epsilon v \ll M\), are

$$\begin{aligned}&m_{\tau ^{\pm }} = y_\tau v (1-\epsilon ^2 v^2 / 2M^2+ {\mathcal {O}}(\epsilon ^2)), \end{aligned}$$
(5)
$$\begin{aligned}&M_{\tau ^{'\pm }} = M (1+\epsilon ^2 v^2 / 2M^2+ {\mathcal {O}}(\epsilon ^2)), \end{aligned}$$
(6)

where the \({\mathcal {O}}(\epsilon ^2)\) terms are suppressed by \(\epsilon ^4 v^4 / M^4\) or \(\epsilon ^2 y _{\tau }^2 v^4 / M^4\). According to Ref. [7], we assume that \(\epsilon \) is small enough to be treated as a tiny perturbation in the mass matrix, but that it exceeds about \(2\times 10^{-7}\) to allow \(\tau ^{'\pm }\) to decay promptly on collider detector. As \(\epsilon \) is a tiny perturbation, M set the mass scale of the VLL \(\tau ^{'\pm }\) and the mixing between the gauge eigenstates \(\tau \) and \(\tau ^{'}\) is quite small, so that \(M_{\tau ^{\pm }} \simeq y_\tau v\), \(m_{\tau ^{'\pm }}\simeq M\) and the SM tau lepton and the vector lepton mass eigenstates \(\tau ^{-}\), \(\tau ^{'-}\) are nearly the same as their corresponding gauge eigenstate \(\tau \), \(\tau ^{'}\), respectively. In addition, we can see that the mixing parameter \(\epsilon \) does not affect the production cross section of the process \(e^{+} e^{-} {\mathop {\longrightarrow }\limits ^{\gamma /Z}} \tau ^{' +} \tau ^{' -}\) from Eq. (7) and the branching ratios of \(\tau ^{'\pm }\) from Eq. (10), so \(\epsilon \) do not affect the cross section of \(e^+ e^- \rightarrow \tau ^{' +} \tau ^{' -}, \tau ^{' +} \rightarrow W^+ \nu _{\tau }, \tau ^{' -} \rightarrow Z \tau ^{-}\) given that the prompt decay of \(\tau ^{'\pm }\). Therefore, we show the potential of future \(e^+ e^-\) colliders for the discovery of \(\tau ^{'}\) in terms of the parameter \(m_{\tau ^{'\pm }}\) in the following sections.

In 2-component fermion representation based on eigenstates [with a metric feature (\(-, +, +, +\))], the singlet VLL model ignores the term of \(\epsilon \) quadratic [3]:

$$\begin{aligned} {\mathcal {L}}_{\mathrm{int}}&=\frac{g s_{W}^{2}}{c_{W}} Z_{\mu } \left( \tau ^{\prime \dagger } \bar{\sigma }^{\mu } \tau ^{\prime } -\bar{\tau }^{\prime \dagger } \bar{\sigma }^{\mu } \bar{\tau }^{\prime }\right) -e A_{\mu }\left( \tau ^{\prime \dagger } \bar{\sigma }^{\mu } \tau ^{\prime } -\bar{\tau }^{\prime \dagger } \bar{\sigma }^{\mu } \bar{\tau }^{\prime }\right) \end{aligned}$$
(7)

where e is QED coupling, g is \(SU(2)_L\) coupling, \(s_W\), \(c_W\) are the sine and cosine of the weak mixing angle with \(e = gs_W\). The \(\tau ^{\prime \pm }\) decay is caused by the mixing parameter \(\epsilon \) and we have the interactions mediating \(\tau ^{\prime \pm }\) decay working to linear order in \(\epsilon \) [3]:Footnote 1

$$\begin{aligned} {\mathcal {L}}_{\mathrm{int}}&= g_{\nu ^{\dagger }_{\tau } \tau ^{\prime }}^{W^{+}} \left[ W_{\mu }^{+}\left( \nu ^{\dagger }_{\tau } \bar{\sigma }^{\mu } \tau ^{\prime }\right) +W_{\mu }^{-}\left( \tau ^{\prime \dagger } \bar{\sigma }^{\mu } \nu _{\tau } \right) \right] \nonumber \\&\quad +g_{\tau ^{\dagger } \tau ^{\prime }}^{Z} Z_{\mu }\left( \tau ^{\dagger } \bar{\sigma }^{\mu } \tau ^{\prime }+\tau ^{\prime \dagger } \bar{\sigma }^{\mu } \tau \right) \nonumber \\&\quad +\left( y_{\tau \bar{\tau }^{\prime }}^{h} h \tau \bar{\tau }^{\prime }+\mathrm{c.c.}\right) \end{aligned}$$
(8)

where

$$\begin{aligned} g_{\nu ^{\dagger }_{\tau } \tau ^{\prime }}^{W^{+}}&=\epsilon m_{W} / m_{\tau ^{\prime }} , \ \ g_{\tau ^{\dagger } \tau ^{\prime }}^{Z} \nonumber \\&=-\epsilon m_{Z} / \sqrt{2} m_{\tau ^{\prime }} ,\ \ y_{\tau \bar{\tau }^{\prime }}^{h}\nonumber \\&=-\epsilon / \sqrt{2} \end{aligned}$$
(9)

The resulting decay widths for \(\tau ^{\prime }\) to SM states are:

$$\begin{aligned} \Gamma \left( \tau ^{\prime \pm } \rightarrow W^{\pm } \nu _{\tau } \right)&=\frac{m_{\tau ^{\prime }}}{32 \pi }\left( 1-r_{W}\right) ^{2} \left( 2+1 / r_{W}\right) \left| g_{\nu ^{\dagger }_{\tau } \tau ^{\prime }}^{W^{+}}\right| ^{2} \nonumber \\ \Gamma \left( \tau ^{\prime \pm } \rightarrow Z \tau ^{\pm } \right)&=\frac{m_{\tau ^{\prime }}}{32 \pi } \left( 1-r_{Z}\right) ^{2}\left( 2+1 / r_{Z}\right) \left| g_{\tau ^{\dagger } \tau ^{\prime }}^{Z}\right| ^{2} \nonumber \\ \Gamma \left( \tau ^{\prime \pm } \rightarrow h \tau ^{\pm } \right)&=\frac{m_{\tau ^{\prime }}}{32 \pi }\left( 1-r_{h}\right) ^{2} \left| y_{\tau \bar{\tau }^{\prime }}^{h}\right| ^{2} \end{aligned}$$
(10)

where \(r_X = m^{2}_X / m^{2}_{\tau ^{'\pm }}\) for \(X = W, Z, h\). In the decays to Z and W, the factors\((2+1 / r_{Z})\) and \((2+1 / r_{W})\) can be understood as coming from the longitudinal (2) and transverse \((1 / r_{X})\) components of the weak vector bosons. The longitudinal components can in turn be understood as essentially the Goldstone modes that are eaten by the vector bosons to obtain their masses. This illustrates the usual Goldstone Equivalence Theorem [16]. The resulting branching ratios only depend on the single parameter \(m_{\tau ^{\prime \pm }}\), as all of the widths are proportional to \(\epsilon ^2\). In Fig. 1, we show the branching ratios of \(\tau ^{\prime \pm } \rightarrow W^{\pm } \nu _{\tau }\), \(Z \tau ^{\pm }\) and \(h \tau ^{\pm }\) as a function of \(m_{\tau ^{\prime \pm }}\) in the singlet VLL model. As expected by the Goldstone Equivalence Theorem, for \(m_{\tau ^{'\pm }} \gg m_h, m_Z, m_W\), the results asymptotically approach: \(\mathrm{BR}\left( \tau ^{\prime \pm } \rightarrow W^{\pm } \nu _{\tau } \right) \) : \(\mathrm{BR}\left( \tau ^{\prime \pm } \rightarrow Z \tau ^{\pm } \right) \) : \(\mathrm{BR}\left( \tau ^{\prime \pm } \rightarrow h \tau ^{\pm } \right) =2\):1:1.

Fig. 1
figure 1

The branching ratios of \(\tau ^{\prime \pm }\) as a function of \(m_{\tau ^{\prime \pm }}\)

Full size image

3 Event generation

We will consider the following \(e^+ e^-\) collider options [17]:

  • ILC with the highest integrated luminosity 4 ab\(^{-1}\) at \(\sqrt{s} = 500\ \hbox {GeV}\);

  • ILC with the highest integrated luminosity 8 ab\(^{-1}\) at \(\sqrt{s} = 1000\ \hbox {GeV}\);

  • CLIC with the highest integrated luminosity 2.5 ab\(^{-1}\) at \(\sqrt{s} = 1500\ \hbox {GeV}\).

Fig. 2
figure 2

Polarized cross sections of \(e^- e^+ \rightarrow \tau ^{'-}\tau ^{'+} \) at different polarization \(P_{e^-}\) and \(P_{e^+}\) for \(m_{\tau ^{'\pm }} = 200\ \hbox {GeV}\) and \(\sqrt{s} =500\ \hbox {GeV}\), and the contour lines stand for these cross sections and their unit is fb

Full size image

Since the polarized \(e^-\) beams and \(e^+\) beams can enhance the cross section effectively, we show the \(e^+ e^- \rightarrow \tau ^{'+}\tau ^{'-} \) cross sections at different polarization \(P_{e^-}\) and \(P_{e^+}\) for \(m_{\tau ^{'}}\) = 200 GeV and \(\sqrt{s}\) = 500 GeV in Fig. 2. We can see the symmetric center of the contour lines is near the point \(\left( P_{e^-}=-0.6, P_{e^+}=+0.6\right) \) rather than \(\left( P_{e^-}=0, P_{e^+}=0\right) \), which is caused by the Z boson mediated in the process \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\). When \(P_{e^-} \rightarrow 1\) and \(P_{e^+}\rightarrow -1\), the polarized cross section tends to the maximum since the polarized cross section \(\sigma _{P_{e^-}P_{e^+}}\) of \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\) can be written as [18],

$$\begin{aligned} \sigma _{P_{e^-}P_{e^+}}= (1-P_{e^-}P_{e^+})\sigma _0\left( 1-P_{eff}A_{LR}\right) , \end{aligned}$$
(11)

where \(P_{e f f}=\frac{P_{e^{-}}-P_{e^{+}}}{1-P_{e^{-}} P_{e^{+}}}\) is the effective polarization, \(\sigma _{RL}\) is the cross section for the completely right-handed polarized \(e^-\) beam (\(P_{e^-} =+1\)) and the completely left-handed polarized \(e^+\) beam (\(P_{e^+} =-1\)), and the cross section \(\sigma _{LR}\) is defined analogously, \(\sigma _0 = \frac{\sigma _{RL}+\sigma _{LR}}{4}\) is the unpolarized cross section, \(A_{LR} = \frac{\sigma _{LR} -\sigma _{RL}}{\sigma _{LR} + \sigma _{RL}}\) is the left-right asymmetry. In principle, only the electron beam needs to be polarized. However, even a small polarization of the positron beam can improve the effective polarization. For example, a \(80\%\) polarization in the electron beam and \(-30\%\) polarization in the positron beam yields an effective initial-state polarization of almost 90\(\%\) [19]. Considering the technical limit, we choose the following polarization in our calculations [17]: \(P_{e^{-}} = 0.8\), \(P_{e^{+}} = -0.3\) for \(\sqrt{s} =500\ \hbox { GeV}\), \(P_{e^{-}} = 0.8\), \(P_{e^{+}} = -0.2\) for \(\sqrt{s} =1000\ \hbox {GeV}\) and \(P_{e^{-}} = 0.8\), \(P_{e^{+}} = 0\) for \(\sqrt{s} =1500\ \hbox {GeV}\).

Fig. 3
figure 3

The left-right asymmetry \(A_{LR}\) as a function of \(m_{\tau ^{\prime \pm }}\) at \(\sqrt{s} = 500\ \hbox {GeV}\), 1000 GeV and 1500 GeV

Full size image

In Fig. 3, we show the value of the left-right asymmetry \(A_{LR}\) as a function of \(m_{\tau ^{'}}\) at \(\sqrt{s} = 500\ \hbox {GeV}\), 1000 GeV and 1500 GeV. We can see that the value of \(A_{LR}\) can reach \(-60\%\), which implies the chirality-violating effect caused by the Z boson.

Table 2 The processes and cross sections of the signal and backgrounds for three benchmark points in pure leptonic channel, where \(L^{\pm } = \ell ^{\pm }, \tau ^{\pm }\). The conjugate processes of the signal and backgrounds have been considered
Full size table

In this work, we choose two decay modes for the signal, that is the pure leptonic channel and fully hadronic channel, the production and decay chain of the signal are given as:

  • pure leptonic: \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\rightarrow (W^+ \bar{\nu }_\tau ) (\tau ^-Z)\rightarrow (\ell ^+ \nu _\ell \bar{\nu }_\tau ) (\tau ^-\ell ^+ \ell ^-)\);

  • fully hadronic: \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\rightarrow (W^+ \bar{\nu }_\tau ) (\tau ^-Z)\rightarrow (jj\bar{\nu }_\tau ) (\tau ^-jj)\).

Based on these signal characters, we analyzed the main backgrounds from the SM processes are \(\tau ^+\tau ^-\), ZZ, Zh, \(ZW^+W^-\), \(t\bar{t}Z\), ZZZ. In order to do quantitative calculation, we implement the singlet VLL model into the FeynRules [20] package to generate the model files in UFO [21] format. Then, we use MG5_aMC_v3.0.1 [22] to calculate the cross sections after decay of the signal and backgrounds and show the results in Table 2. The parton level events of the signal and backgrounds are required to pass through the basic cuts as follows:

$$\begin{aligned}&\Delta R(x,y)> 0.4\ , \quad x,y = L(\ell , \tau ), j(g,u,d,c,s), b \\&p_{T}^L> 10 \ \text {GeV}\ , \quad |\eta _L|<2.5 \\&p_{T}^b> 20 \ \text {GeV}\ , \quad |\eta _b|<2.5 \\&p_{T}^j > 20 \ \text {GeV}\ , \quad |\eta _j|<5.0 \end{aligned}$$

where \(p_T\) denotes the transverse momentum, meanwhile \(\Delta R(x,y) =\sqrt{(\Delta \phi )^2 + (\Delta \eta )^2} \) with \( \Delta \phi \) the difference of azimuthal angle between object x and y and \(\Delta \eta \) the difference of pseudo-rapidity between them. These basic cuts are used to simulate the geometrical acceptance and detection threshold of the detector.

Considering the limits of current experiments and collision energy, we take these parameter spaces \(m_{\tau ^{\prime \pm }} \in [180,250]\ \hbox {GeV}\) for \(\sqrt{s} = 500\ \hbox {GeV}\), \(m_{\tau ^{\prime \pm }} \in [240,500]\ \hbox {GeV}\) for \(\sqrt{s} =1000\ \hbox {GeV}\) and \(m_{\tau ^{\prime \pm }} \in [450,750]\ \hbox {GeV}\) for \(\sqrt{s} =1500\ \hbox {GeV}\), we also choose three benchmark points \(m_{\tau ^{\prime \pm }} = 200\ \hbox {GeV}\), \(m_{\tau ^{\prime \pm }}\) = 350 GeV and \(m_{\tau ^{\prime \pm }} =600\ \hbox {GeV}\), respectively. The relevant SM input parameters [23] are taken as follows:

$$\begin{aligned}&m_t = 173.0~\mathrm{GeV},\quad m_{Z} =91.1876 ~\mathrm{GeV}, \quad m_h =125 ~\mathrm{GeV}, \\&\sin ^{2}\theta _W = 0.231,\quad \alpha (m_Z) = 1/128.877. \end{aligned}$$

Note that the fine-structure constant \(\alpha \) is chosen at the \(m_Z\) scale in our simulation, which will not lead to the correct W boson mass at the tree level. But the effect coming from different values of \(\alpha \) is negligible for detector simulation.

Fig. 4
figure 4

The signal cross sections as a function of \(\sqrt{s}\) for \(m_{\tau ^{\prime \pm }} = 200, 350, 600\ \hbox {GeV}\)

Full size image

In Fig. 4, we show the signal cross sections as a function of \(\sqrt{s}\) for \(m_{\tau ^{\prime \pm }} = 200, 350, 600\ \hbox {GeV}\). We can see that the cross sections increase sharply at the threshold and then decrease with the center-of-mass energy \(\sqrt{s}\), which comes from the center-of-mass energy suppression of s-channel production process.

Fig. 5
figure 5

The cross sections of the signal process for \(m_{\tau ^{\prime \pm }} = 200\ \hbox {GeV}\) and background processes as a function of \(\sqrt{s}\)

Full size image
Fig. 6
figure 6

The Feynman diagram of \(e^+ e^- \rightarrow \tau ^{\prime +}\tau ^{\prime -}\) followed by the subsequent decay chains in pure leptonic chanel or fully hadronic channel

Full size image
Fig. 7
figure 7

Normalized distributions of the and \(\Delta R(\tau _1,\ell _1)\) in the signal and backgrounds at \(\sqrt{s}=500\ \hbox {GeV}\). The solid lines stand for signal events, dashed lines stand for background events and black arrows indicate our selection cuts

Full size image

In Fig. 5, we show the cross sections before decay of the signal process for \(m_{\tau ^{\prime \pm }} = 200\ \hbox {GeV}\) and background processes as a function of \(\sqrt{s}\). We can see that the cross sections of backgrounds \(\tau \tau \), ZZ, Zh are larger than the signal and the dominant background \(\tau \tau \) is about \(10^3\) times larger than the signal. In order to improve the signal significance, it is necessary to perform the detailed detector simulation and choose some effective cuts to suppress these backgrounds.

In the detector simulation of final states, we transmit these parton-level events to Pythia 8 [24] for showering and hadronization. Then we make a fast detector simulations by Delphes [25] and cluster jets by Fastjet [26] with the anti-\(K_t\) algorithm [27], where the distance parameter \(\Delta R = 0.4\). Finally, we analyse the reconstructed-level events by using MadAnalysis 5 [28, 29]. Besides, we use the package EasyScan_HEP [30] to connect these programs and scan the parameter space. In order to quantimize the observability, we evaluate the statistical significance \(({\mathcal {S}})\) by using the Poisson formula [31] as follow:

$$\begin{aligned} {\mathcal {S}}=\sqrt{2 {\mathcal {L}}\left[ \left( \sigma _{S}+\sigma _{B}\right) \ln \left( 1+\frac{\sigma _{S}}{\sigma _{B}}\right) -\sigma _{S}\right] } \end{aligned}$$
(12)

where \({\mathcal {L}}\) is the integrated luminosity and \(\sigma _{S}\), \(\sigma _{B}\) are the signal and background cross sections after all cuts, respectively. Here we define the exclusion limits as \({\mathcal {S}} = 2\), the possible evidence as \({\mathcal {S}} = 3\) and the discovery significance as \({\mathcal {S}} = 5\).

Systematic uncertainties are known to become dominant especially at higher luminosities, so we estimate the precision on the singlet VLL mass in case of a discovery by the following significance formula considering uncertainty for the background [31]:

Table 3 Summary of the cut schemes, where \(\tau \) stands for the \(\tau \)-tagging jet, \(j=g,u,d,c,s\) stands for light flavour jets, b stands for the b-tagging jet, \(\ell =e,\mu \)
Full size table
Table 4 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=200\ \hbox {GeV}\), \(\sqrt{s}=500\ \hbox {GeV}\)
Full size table
Table 5 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=350\ \hbox {GeV}\), \(\sqrt{s}=1000\ \hbox {GeV}\)
Full size table
Table 6 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=600\ \hbox {GeV}\), \(\sqrt{s}=1500\ \hbox {GeV}\)
Full size table
$$\begin{aligned} {\mathcal {S}}=\sqrt{2\left( {\mathcal {L}}\left( \sigma _{S}+\sigma _{B}\right) \ln \left[ \frac{\left( \sigma _{S}+\sigma _{B}\right) \left( \sigma _{B} +{\mathcal {L}}\Delta _{b}^{2}\right) }{\sigma _{B}^{2}+{\mathcal {L}} \left( \sigma _{S}+\sigma _{B}\right) \Delta _{b}^{2}}\right] -\frac{\sigma _{B}^{2}}{\Delta _{b}^{2}}\ln \left[ 1+\frac{{\mathcal {L}} \Delta _{b}^{2}\sigma _{S}}{\sigma _{B}\left( \sigma _{B}+{\mathcal {L}} \Delta _{b}^{2}\right) }\right] \right) } \end{aligned}$$
(13)

where \(\Delta _{b}\) stands for the systematic uncertainties of backgrounds and we choose \(\Delta _{b}=0.3*\sigma _{B}\) in the pure lepton channel and \(\Delta _{b}=0.5*\sigma _{B}\) in the hadronic channel.

4 Numerical results

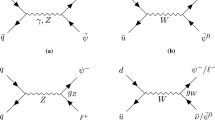
In this section, we will display the signal significance and the related excluding and discovering capability in the pure leptonic channel and fully hadronic channel at \(e^+ e^-\) colliders with \(\sqrt{s} = 500\), 1000 and 1500 GeV. We show the Feynman diagrams of the signal followed by the pure leptonic decay in Fig. 6a and followed by the fully hadronic decay in Fig. 6b.

Fig. 8
figure 8

The contour plots of \({\mathcal {S}}=2\) (blue solid line), \({\mathcal {S}}=3\) (black solid line) and \({\mathcal {S}}=5\) (red solid line) in the \({\mathcal {L}}\sim m_{\tau ^{\prime \pm }}\) plane for pure leptonic channel. The horizontal dashed black line is the highest integrated luminosity, and the horizontal dashed blue (red) line stands for the integrated luminosity for excluding (discovering) the mass region \(m_{\tau ^{\prime \pm }} \in [180,240]\ \hbox {GeV}\) in a, [240,450] GeV in b and [450,700] GeV in c. For discovery \({\mathcal {S}}=5\), the surrounding red band corresponds to the significance considering the systematic uncertainties \(\sigma _B=0.3*B\)

Full size image
Table 7 The processes and cross sections of the signal and backgrounds for three benchmark points in fully hadronic channel, where \(L^{\pm } = \ell ^{\pm }, \tau ^{\pm }\). The conjugate processes of the signal and backgrounds have been considered
Full size table
Fig. 9
figure 9

Same as Fig. 7 but for normalized distributions of the and \(E_T\) of signal and backgrounds in fully hadronic channel at \(\sqrt{s}=500\ \hbox {GeV}\)

Full size image
Table 8 Same as Table 3 but for fully hadronic channel
Full size table
Table 9 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=200\ \hbox {GeV}\), \(\sqrt{s}=500\ \hbox {GeV}\)
Full size table
Table 10 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=350\ \hbox {GeV}\), \(\sqrt{s}=1000\ \hbox {GeV}\)
Full size table
Table 11 Cut flows of the signal and backgrounds at \(m_{\tau ^{\prime \pm }}=600\ \hbox {GeV}\), \(\sqrt{s}=1500\ \hbox {GeV}\)
Full size table
Fig. 10
figure 10

Same as Fig. 8, but for the fully hadronic channel and the surrounding red band corresponds to the significance considering the systematic uncertainties \(\sigma _B=0.5*B\)

Full size image

4.1 pure leptonic channel

We give the processes of the signal and backgrounds in Table 2. We can see that the signal events satisfy the following features:

  1. (i)

    one lepton \(\tau \) and one neutrino \(\nu _\tau \) (i.e., missing energy at the detector level) are directly from the VLL decay;

  2. (ii)

    two leptons (labeled as \(\ell \) and \(\ell =e,\mu \)) from the Z boson, one lepton and one neutrino from W boson.

According to the features of the signal and backgrounds, we choose the missing energy and the separation \(\Delta R(\tau _1,\ell _1)\)Footnote 2 as cut criterions. As an example, we show their normalized distributions for the three benchmark points of the signal and backgrounds at \(\sqrt{s}=500\ \hbox {GeV}\) in Fig. 7. According to the behaviours of these distributions, we impose the cut schemes in Table 3 to enhance the signal significance for three different \(e^+ e^-\) options, i.e., ILC with \(\sqrt{s}=500\ \hbox {GeV}\), ILC with \(\sqrt{s}=1000\ \hbox {GeV}\) and CLIC with \(\sqrt{s}=1500\ \hbox {GeV}\).

Table 12 Comparison of the excluding and discovering capability in the pure leptonic and the fully hadronic decay channels of electroweak gauge bosons for \(\sqrt{s}=500\hbox { GeV}\) at ILC. The numbers in parentheses indicate the uncertainties of integrated luminosity
Full size table
Table 13 Same as Table 12 but for \(\sqrt{s}=1000\hbox { GeV}\) at ILC
Full size table
Table 14 Same as Table 12 but for \(\sqrt{s}=1500\hbox { GeV}\) at CLIC
Full size table

We show the cut flows of the signal and backgrounds at \(\sqrt{s}=500, 1000, 1500\ \hbox {GeV}\) in Tables 4, 5, 6, respectively. The bottom row named “Total Eff.” stands for the ratio of cross section at “Cut-2” over that at “Basic cut”. From these tables, we can see that the selected cuts can suppress the backgrounds and isolate the signal effectively. In Fig. 8a–c, we show the \({\mathcal {S}}\)= 2, 3, 5 lines in the \({\mathcal {L}}\sim m_{\tau ^{\prime \pm }}\) plane at \(\sqrt{s}\)=500, 1000, 1500 GeV, respectively. We can see that the required integrated luminosity increases with \(m_{\tau ^{\prime \pm }}\) increasing and sharply rises when \(m_{\tau ^{\prime \pm }}\) approaches to the threshold value, that is mainly because the signal cross section quickly decreases when \(m_{\tau ^{\prime \pm }}\) increases. If we consider the systematic uncertainties of backgrounds \(\sigma _B=0.3*B\), we can see that the integrated luminosities for discovery significance are required to increase by about 20%, 15%, 60% for the same \(m_{\tau ^{\prime \pm }}\) at \(\sqrt{s} = 500, 1000, 1500\ \hbox {GeV}\), respectively. The greater impact of systematic uncertainties on the case of \(\sqrt{s} = 1500\ \hbox {GeV}\) is due to the smaller signal to noise ratio in this case. At the highest integrated luminosities, the highest masses of \(\tau ^{\prime \pm }\) can be probed to 245 GeV at 500 GeV with 4 ab\(^{-1}\), 475 GeV at 1000 GeV with 8 ab\(^{-1}\) and 680 GeV at 1500 GeV with 2.5 ab\(^{-1}\).

4.2 Fully hadronic channel

We give the processes of the signal and backgrounds in Table 7. We can see that the signal events satisfy the following features:

  1. (i)

    one \(\tau \) lepton and one \(\tau \) neutrino \(\nu _\tau \) (i.e., missing energy at the detector level) are directly from the VLL decay;

  2. (ii)

    two jets (labeled as j and \(j=d,u,s,c,\bar{c},\bar{s},\bar{u},\bar{d},g\)) come from the W boson and two jets come from the Z boson.

According to the features of the signal and backgrounds, we choose the following kinematical variables as cut criterions: The missing transverse energy and the total transverse energy \(E_T\), where

$$\begin{aligned} E_{T} =\sum _{visible~particles}\left| \vec {P}_{T}\right| \end{aligned}$$

\(`` \left| \,\,\right| \)” for the magnitude of \(\vec {P}_{T}\).

As an example, we show the normalized distributions of the missing transverse energy and the total transverse energy \(E_T\) of the signal and backgrounds \(\sqrt{s}=500\ \hbox {GeV}\) after only the basic cut in Fig. 9. Based on these distributions, we impose the cuts to enhance the signal significance shown in Table 8.

We show the cut flows of the signal and backgrounds at \(\sqrt{s}=500, 1000, 1500\ \hbox {GeV}\) in Tables 9, 10, 11, respectively. We can see that the total cut efficiency of signal can reach more than \(10\%\) after all the cuts, while the total cut efficiencies of the backgrounds are reduced to less than 3%. In Fig. 10a–c, we show the significance contour lines \({\mathcal {S}}= 2\), 3, 5 in the \({\mathcal {L}}\sim m_{\tau ^{\prime \pm }}\) plane at \(\sqrt{s}=500\), 1000, 1500 GeV. If we consider the systematic uncertainties of backgrounds \(\sigma _B=0.5*B\), we can see that the integrated luminosities for discovery significance are required to increase by about 15%, 10%, 30% for the same \(m_{\tau ^{\prime \pm }}\) at \(\sqrt{s} = 500, 1000, 1500\ \hbox {GeV}\), respectively. At the highest integrated luminosities, the highest masses of \(\tau ^{\prime \pm }\) can be probed to 248 GeV at 500 GeV with 4 ab\(^{-1}\), 495 GeV at 1000 GeV with 8 ab\(^{-1}\) and 745 GeV at 1500 GeV with 2.5 ab\(^{-1}\).

5 Summary

In the singlet VLL model, we investigate the VLL through the process \(e^+ e^- \rightarrow \tau ^{'+} \tau ^{'-}\) followed by the two decay modes of the electroweak gauge bosons at \(e^+e^-\) collider. We perform a detailed detector simulation and choose the suitable kinematic cuts to enhance the signal significance effectively. For clarity, we display the comparison of the excluding and discovering capability in the two decay channels at different colliders with various center of mass energy in Tables 12, 13, 14.

From these tables, we can see that the process \(e^+ e^- \rightarrow \tau ^{'+}\tau ^{'-}\), \(\tau ^{'+} \rightarrow W^+ \bar{\nu }_\tau , \tau ^{'-}\rightarrow \tau ^-Z\) in the pure leptonic channel needs higher integrated luminosities for excluding or discovering the VLL \(\tau ^{\prime \pm }\) compared to the fully hadronic channel. Obviously, it is more hopeful to exclude and discover the singlet VLL through the fully hadronic channel at the \(e^+ e^-\) colliders. Besides, we can see that the future \(e^+e^-\) colliders will extend the search of the LHC and bring us a chance to detect the singlet VLL.