One-loop corrections to the two-body decays of the charged Higgs bosons in the real and complex NMSSM

Abstract

We evaluate the full next-to-leading order supersymmetric (SUSY) electroweak and SUSY-QCD corrections to the on-shell two-body decays of the charged Higgs bosons in the framework of the next-to-minimal supersymmetric extension of the Standard Model (NMSSM) allowing also for CP violation. We furthermore provide the possibility to choose between different renormalization schemes in the electroweakino and the squark and slepton sectors. Our corrections are implemented in the code NMSSMCALCEW and thus complete the one-loop corrections of the charged Higgs boson decays which so far only included the state-of-the-art QCD corrections and the resummed SUSY-electroweak and SUSY-QCD corrections. We investigate the impact of the NLO corrections including the newly computed higher-order corrections for each decay mode in a wide range of the parameter space that is allowed by the theoretical and experimental constraints as well as the effect of CP violation and the dependence on the choice of the renormalization scheme. The new version of NMSSMCALCEW is made publicly available.

1 Introduction

While the Higgs boson with a mass of 125 $\mathrm{GeV}$ [1] discovered by the LHC experiments ATLAS [2] and CMS [3] behaves very Standard Model (SM)-like [4, 5] the pending open questions within the SM call for extensions of the Higgs sector. The lacking direct discovery of any new physics sign so far forces us to focus more and more on the indirect discovery of physics beyond the SM which in turn requires precise predictions of the considered observables.

Among the most popular and best studied models beyond the SM is supersymmetry (SUSY) [6,7,8,9,10,11,12,13,14,15,16], which requires at least two complex Higgs doublets. This minimal supersymmetric SM (MSSM) [17,18,19,20] is extended by an additional complex singlet superfield in the next-to-minimal supersymmetric SM (NMSSM) [9, 21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. With a Higgs sector consisting of seven Higgs bosons, three neutral CP-even, two neutral CP-odd and two charged Higgs bosons, it entails a rich phenomenology. Moreover, the NMSSM features CP violation in the Higgs sector already at tree level that still allows for non-zero NMSSM-specific CP-violating phases despite the strong experimental constraints from the measurement of the electron electric dipole moment (EDM) by the ACME collaboration [36] which is due to cancellations of the NMSSM-specific contributions to the EDMs [37]. CP violation is one of the three Sakharov conditions [38] and hence a key ingredient for electroweak baryogenesis. In extended Higgs sectors, charged Higgs bosons play an important role. Their discovery would be a clear manifestation of extended Higgs sectors. Moreover, their possible decay channels induce interesting non-SM decay signatures, besides those in SUSY pairs, in particular modes with a massive gauge boson and a neutral Higgs boson in the final state.

The very SM-like nature of the discovered Higgs boson calls for sophisticated experimental techniques together with precise theoretical predictions in order to reveal new physics signs. In the context of the NMSSM, various radiative corrections to Higgs observables have been calculated. More specifically in the context of Higgs boson decay widths, the next-to-leading order (NLO) SUSY-electroweak (EW) and SUSY-QCD corrections to the decays of CP-odd Higgs bosons of the CP-conserving NMSSM into stop pairs have been computed in [39]. The full one-loop renormalization of the CP-conserving NMSSM has been worked out in [40, 41] together with the computation of the one-loop two-body Higgs decays in the on-shell (OS) renormalization scheme. In [42] a generic calculation of the two-body decays widths at full one-loop level was provided in the $\overline{\text{ DR }}$ scheme. The full one-loop corrections for the neutral Higgs decays into fermions and gauge bosons was performed in [43] in the framework of the CP-violating NMSSM and combined with the leading QCD corrections. More recently, the effects of Sudakov logarithms on fermionic decays of heavy Higgs bosons, which appear though radiative corrections of electroweak gauge bosons, have been studied in Ref. [44]. In [45], members of our group completed the evaluation of the NLO SUSY-EW and SUSY-QCD corrections to the full set of two-body on-shell decays of the neutral Higgs bosons in the CP-violating NMSSM, including the state of the art QCD corrections. For the Higgs-to-Higgs decays, the complete one-loop corrections [46] and two loop corrections of order ${\mathcal {O}}(\alpha _{s}\alpha _{t})$ [47] have been calculated in both the CP-conserving and the CP-violating NMSSM. As for the charged Higgs bosons, authors of our group have computed the SUSY-EW corrections to the charged Higgs two-body decays into a neutral Higgs boson and a $W^+$ boson and studied the gauge dependence arising from the mixing of different loop orders due to the inclusion of mass corrections to the external Higgs boson [48] in order to comply with phenomenological constraints. The authors of [49] discussed this problem further and proposed two strategies to preserve or restore gauge invariance.

In this work, we complete the one-loop higher-order corrections to the on-shell charged Higgs boson decays both in the CP-conserving and CP-violating NMSSM. In the previous implementation in our code NMSSMCALC [53], which computes the NMSSM Higgs mass spectrum and decays in both the CP-conserving and CP-violating case, the charged Higgs boson decay widths so far only included the state-of-the-art QCD corrections for the quark final states and the resummed SUSY-QCD and SUSY-electroweak corrections in the quark and lepton final states, respectively. The aim of this paper is to improve the accuracy for the predictions of the charged Higgs decay widths by computing the remaining one-loop SUSY-electroweak and SUSY-QCD corrections to all charged Higgs boson decays into on-shell two-particle final states in the framework of the CP-conserving and CP-violating NMSSM. More specifically, we evaluate the complete one-loop corrections to the decays into SM fermions, electroweakinos, sleptons and squarks. The one-loop corrections are based on the renormalization schemes that we have introduced and applied in Refs. [45, 47, 50,51,52]. In particular, we use a mixed $\overline{\text{ DR }}$-OS scheme in the Higgs sector and have the possibility to choose between OS and $\overline{\text{ DR }}$ renormalization in the electroweakino sector and in the squark and slepton sectors. This allows us to give a rough estimate of the remaining theoretical uncertainties due to missing higher-order corrections. The possibility to choose between different renormalization schemes and to include CP violation is new with respect to existing results in the literature.

Our newly computed higher-order corrections to the charged Higgs decays as well as those obtained previously in [48] are included in the Fortran code NMSSMCALCEW [45]. The program is based on NMSSMCALC [53] that has been derived by extending the Fortran code HDECAY [54, 55] to the NMSSM and as such contains the state-of-the-art QCD corrections and relevant off-shell decays as well as higher-order SUSY corrections through effective couplings. In the first version of NMSSMCALCEW we already included the SUSY-EW corrections to the neutral NMSSM Higgs boson decays of the CP-violating NMSSM published in Ref. [45] as well as their SUSY-QCD corrections to the coloured final states. The code NMSSMCALCEW with now also the higher-order corrections to the charged Higgs boson decays is available at the url:

$$\begin{aligned} \mathtt{http.//www.itp.kit.edu/\!\sim \! maggie/NMSSMCALCEW/} \end{aligned}$$

With our implemented corrections in NMSMMCALCEW we compute the decay widths and branching ratios of the charged Higgs bosons in the CP-conserving and CP-violating NMSSM and investigate the impact of our computed one-loop corrections. We start by investigating the relative size of the SUSY-EW and SUSY-QCD corrections, taking into account the recent theoretical and experimental constraints. In our analysis we find that the newly computed corrections are significant and can also become very large for some of the final states in specific corners of the parameter space. This shows the importance of the corrections for a meaningful interpretation of the experimental results both in direct as well as indirect searches for new physics. Subsequently, we analyse the new features of our results with respect to existing results, i.e. the effect of CP violation on the corrections to the decay widths and the impact of the choice of the renormalization scheme on the one-loop results.

The paper is organized as follows. In Sect. 2, we introduce the NMSSM at tree level to fix our notation for the higher-order computations. In Sect. 3, we briefly discuss the renormalization of the Higgs sector, the electroweakino and the squark sector. In Sect. 4 we move on to the calculations of the radiative corrections to the decay widths of the on-shell two-body decays of the charged Higgs boson. Our numerical analysis is presented in Sect. 5. Conclusions are given in Sect. 6.

2 The NMSSM at tree level

In this section, we briefly introduce the model and set up the notation used throughout the paper. Our notation and conventions follow those already used and explained in detail in our previous works [45,46,47,48, 50,51,52, 56]. We work in the framework of the scale-invariant NMSSM, in which the superpotential is constrained by a ${\mathbb {Z}}_3$ symmetry. The NMSSM is obtained from the MSSM by adding a gauge-singlet chiral superfield ${{\hat{S}}}$ to the MSSM field content. Since the new additional field is not charged under the $SU(2)_L \times U(1)_Y$ symmetry, the modification of the supersymmetric Lagrangian with respect to the MSSM only arises in the superpotential,

$$\begin{aligned} {\mathcal {W}}_{\mathrm{NMSSM}}={\mathcal {W}}_{\mathrm{MSSM}} -\epsilon _{ij} \lambda {\hat{S}} {\hat{H}}_d^i{\hat{H}}_u^j+\frac{1}{3}\kappa {{\hat{S}}}^3, \end{aligned}$$

(1)

where ${{\hat{H}}}_u, {{\hat{H}}}_d$ are the Higgs doublet superfields and $\epsilon _{ij}$ ($i,j=1,2$) is the totally antisymmetric tensor, with $\epsilon _{12}= \epsilon ^{12}=1$, and i, j denote the indices of the fundamental $SU(2)_L$ representation. Here and in the following we sum over repeated indices. The dimensionless NMSSM-specific parameters $\lambda$ and $\kappa$ are complex in the CP-violating NMSSM. The MSSM superpotential ${\mathcal {W}}_{\mathrm{MSSM}}$ is written in terms of the quark and lepton chiral superfields ${{\hat{Q}}}, {{\hat{L}}},{{\hat{U}}}, {{\hat{D}}}$ and ${{\hat{E}}}$ as

$$\begin{aligned} {\mathcal {W}}_\text {MSSM} = \epsilon _{ij} [y_e \hat{H}^i_d \hat{L}^j \hat{E}^c + y_d \hat{H}_d^i \hat{Q}^j \hat{D}^c - y_u \hat{H}^i_u \hat{Q}^j \hat{U}^c], \end{aligned}$$

(2)

where, for simplicity, we neglect colour and generation indices. Assuming flavour conservation, the Yukawa couplings $y_u,\ y_d$ and $y_e$ are diagonal 3$\times$3 matrices in flavour space. In accordance with the applied ${\mathbb {Z}}_3$ symmetry, the MSSM parameter $\mu$ has been set to zero.

In the NMSSM, the soft supersymmetry (SUSY) breaking Lagrangian reads

$$\begin{aligned} {\mathcal {L}}_{\mathrm{soft,NMSSM}}&= -m_{H_d}^2 H_d^\dagger H_d - m_{H_u}^2 H_u^\dagger H_u - m_{\tilde{Q}}^2 \tilde{Q}^\dagger \tilde{Q} \nonumber \\&\quad - m_{\tilde{L}}^2 \tilde{L}^\dagger \tilde{L} - m_{\tilde{u}_R}^2 \tilde{u}_R^* \tilde{u}_R - m_{\tilde{d}_R}^2 \tilde{d}_R^* \tilde{d}_R \nonumber \\&\quad - m_{\tilde{e}_R}^2 \tilde{e}_R^* \tilde{e}_R - \Bigg (\epsilon _{ij} [y_e A_e H_d^i \tilde{L}^j \tilde{e}_R^* \nonumber \\&\quad + y_d A_d H_d^i \tilde{Q}^j \tilde{d}_R^* - y_u A_u H_u^i \tilde{Q}^j \tilde{u}_R^*] + \mathrm {h.c.}\Bigg ) \nonumber \\&\quad -\frac{1}{2}\Bigg (M_1 \tilde{B}\tilde{B} + M_2 \tilde{W}_j\tilde{W}_j + M_3 \tilde{G}\tilde{G} + \mathrm {h.c.}\Bigg ) \nonumber \\&\quad - m_S^2 |S|^2 + \Bigg (\epsilon _{ij} \lambda A_\lambda S H_d^i H_u^j - \frac{1}{3} \kappa A_\kappa S^3 + \mathrm {h.c.}\Bigg ) , \end{aligned}$$

(3)

F where $\tilde{Q}=(\tilde{u}_L,\tilde{d}_L)^T$, $\tilde{L}=({\tilde{\nu }}_L,\tilde{e}_L)^T$, $H_d$ and $H_u$ are the complex scalar components of the chiral superfields $\hat{Q}$, $\hat{L}$, ${\hat{H}}_d$ and ${\hat{H}}_u$, respectively. Similarly, $\tilde{u}_R$, $\tilde{d}_R$ and $\tilde{e}_R$ denote the complex scalar components of the right-handed quark and lepton chiral superfields. Moreover, $\tilde{B},\ \tilde{W}_i$ $(i=1,2,3)$ and $\tilde{G}$ represent the bino, wino and gluino fields, with masses $M_j\ (j=1,2,3)$, respectively. Finally, the parameters $m_X^2$ are the squared soft SUSY-breaking masses of the fields $X=S, H_d, H_u, \tilde{Q}, \tilde{u}_R, \tilde{d}_R, \tilde{L}, \tilde{e}_R$. The terms $A_{\alpha }\ (\alpha =u, d, e, \lambda ,\kappa )$ are the soft SUSY-breaking trilinear couplings. In the CP-violating NMSSM, the trilinear couplings and the gaugino mass parameters $M_j\ (j=1,2,3)$ are complex.

The Higgs sector The tree-level Higgs potential derived from the F- and D-terms in the supersymmetric Lagrangian, and the soft SUSY-breaking Lagrangian, Eq. (3), reads

$$\begin{aligned} V_{H}&=|\lambda S|^2\left( H_{u}^\dagger H_u+H_{d}^\dagger H_d\right) \nonumber \\&\quad +\left| -\epsilon _{ij}\lambda \left( H_d^iH_u^j\right) +\kappa S^2\right| ^2 \nonumber \\&\quad +\frac{1}{2}g_2^2\left| H_u^\dagger H_d\right| ^2+\frac{1}{8}(g_1^2+g_2^2)\left( H_u^\dagger H_u-H_d^\dagger H_d\right) ^2 \nonumber \\&\quad +m_{H_u}^2H_u^\dagger H_u+m_{H_d}^2H_d^\dagger H_d+m_S^2\left| S\right| ^2\nonumber \\&\quad + \left[ -\epsilon _{ij}\lambda A_\lambda \left( H_d^iH_u^j\right) S +\frac{1}{3}\kappa A_\kappa S^3+\mathrm{h.c.}\right] , \end{aligned}$$

(4)

where $g_1$ and $g_2$ are the gauge couplings of the $U(1)_Y$ and $SU(2)_L$ symmetry, respectively. The complex scalar Higgs doublet fields $H_u$ and $H_d$ and the complex singlet field S are expressed in terms of the component fields and vacuum expectation values (VEVs) as

$$\begin{aligned} H_u&= e^{i\varphi _u}\begin{pmatrix} h_u^+\\ \frac{1}{\sqrt{2}}(v_u+h_u+ia_u) \end{pmatrix},\nonumber \\ H_d&= \begin{pmatrix} \frac{1}{\sqrt{2}}(v_d+h_d+ia_d) \\ h_d^- \end{pmatrix},\nonumber \\ S&=\frac{1}{\sqrt{2}}e^{i\varphi _s}(v_s+h_s+ia_s) \;, \end{aligned}$$

(5)

where $v_u, v_d$ and $v_s$ are the VEVs of $H_u$, $H_d$, and S, respectively. The two CP-violating phases $\varphi _u$ and $\varphi _s$ describe the phase differences between the VEVs. Following Refs. [47, 50,51,52], we set the phases of the Yukawa couplings to zero and rephase the left- and right-handed up-quark fields as $u_L \rightarrow e^{-i \varphi _u} u_L$ and $u_R \rightarrow e^{i\varphi _u} u_R$, so that the quark and lepton mass terms yield real masses. Inserting Eq. (5) into the gauge sector of the Lagrangian, we obtain the masses the charged gauge bosons $W^\pm$ and the neutral Z boson, respectively,

$$\begin{aligned} M_W=\frac{1}{2}vg_2 \quad \text{ and } \quad M_Z=\frac{1}{2}v\sqrt{g_1^2+g_2^2}, \end{aligned}$$

(6)

with the SM VEV v $\simeq 246 \,\mathrm{GeV}$ being related to $v_d$ and $v_u$ as

$$\begin{aligned} v^2=v_u^2+v_d^2, \end{aligned}$$

(7)

with

$$\begin{aligned} \tan \beta = \frac{v_u}{v_d}. \end{aligned}$$

(8)

The weak mixing angle $\theta _W$ is defined as

$$\begin{aligned} \cos \theta _W = \frac{M_W}{M_Z}. \end{aligned}$$

(9)

Substituting Eq. (5) into Eq. (4), we can express the Higgs potential as

$$\begin{aligned} V_H= & {} V_H^{\text {const}} + t_{\phi _i} \phi _i + \begin{pmatrix} h_d^+&h_u^+ \end{pmatrix} \mathbf {M_{H^{\pm }}} \begin{pmatrix} h_d^- \\ h_u^- \end{pmatrix} \nonumber \\&+ \frac{1}{2} \phi \mathbf {M_{\phi \phi }} \phi ^T + \lambda _{ijk}^{\phi ^3}\phi _i\phi _j\phi _k + V_H^{\phi ^4}, \end{aligned}$$

(10)

where $\phi =(h_d,h_u,h_s,a_d,a_u,a_s)$, $i,j,k=1,\ldots ,6$. Explicit expressions for the tadpoles $t_{\phi _i}$ and the mass matrix squared $\mathbf {M_{\phi \phi }}$ can be found in Refs. [50, 56]. The trilinear couplings $\lambda _{ijk}^{\phi ^3}$ have been derived in Refs. [46, 47]. The constant and quartic terms are summarized in $V_H^{\text {const}}$ and $V_H^{\phi ^4}$, respectively.

The charged Higgs mass matrix in the ’t Hooft-Feynman gauge, see [45], is given by

$$\begin{aligned} \mathbf {M_{H^{\pm }}}&= \frac{1}{2} \begin{pmatrix} {t_{\beta }}&{} 1 \\ 1 &{} 1/{t_{\beta }}\end{pmatrix} \bigg [ M_W^2 s_{2\beta } + \frac{|\lambda |v_s}{\cos ( \varphi _\lambda +\varphi _u+ \varphi _s) }\nonumber \\&\quad \times \left( \sqrt{2} \,\text {Re}\,A_\lambda +|\kappa |v_s \cos (\varphi _\kappa +3\varphi _s) \right) \nonumber \\&\quad -\frac{2 |\lambda |^2 M_W^2 s_{\theta _W}^2}{e^2}s_{2\beta } \bigg ] + M_W^2 \begin{pmatrix} {c_{\beta }}^2 &{} -{c_{\beta }}{s_{\beta }}\\ -{c_{\beta }}{s_{\beta }}&{} {s_{\beta }}^2 \end{pmatrix}, \end{aligned}$$

(11)

where $\varphi _\lambda$ and $\varphi _\kappa$ are the angular arguments of $\lambda$ and $\kappa$, respectively. Here and in the following, we use the shorthand notation $t_x\equiv \tan x, s_x \equiv \sin x, c_x \equiv \cos x$. Rotating the interaction states $h_d^\pm ,h_u^\pm$ by a rotation with the angle $\beta _c=\beta$, we obtain the charged Higgs boson $H^\pm$ with mass

$$\begin{aligned} M_{H^\pm }^2= & {} M_W^2+\frac{|\lambda |v_s}{s_{2\beta }\cos ( \varphi _\lambda +\varphi _u+ \varphi _s) } \nonumber \\&\times \left( \sqrt{2} \text {Re}\,A_\lambda +|\kappa |v_s \cos ( \varphi _\kappa + 3\varphi _s) \right) -\frac{2 |\lambda |^2 M_W^2 s_{\theta _W}^2}{e^2} \end{aligned}$$

(12)

and the charged Goldstone boson $G^\pm$ mass given by the charged $W^+$ mass in the ’t Hooft–Feynman gauge that we apply.

The neutral Higgs boson mass eigenstates are obtained via the diagonalization of the mass matrix squared $\mathbf {M_{\phi \phi }}$ by an orthogonal matrix ${\mathcal {R}}$,

$$\begin{aligned}&{\text {diag}}(m_{h_1}^2, m_{h_2}^2,m_{h_3}^2,m_{h_4}^2, m_{h_5}^2,M_Z^2)= {\mathcal {R}} \mathbf {M_{\phi \phi }} {\mathcal {R}}^T, \end{aligned}$$

(13)

$$\begin{aligned}&(h_1,h_2,h_3,h_4,h_5,G^0)^T = {\mathcal {R}} (h_d, h_u, h_s, a_d, a_u, a_s)^T, \nonumber \\ \end{aligned}$$

(14)

where $G^0$ is the neutral Goldstone boson with its mass given by the neutral Z boson mass in the applied ’t Hooft–Feynman gauge, and the tree-level neutral Higgs boson masses are ordered as $m_{h_1} \le \cdots \le m_{h_5}$.

The tree-level Higgs sector of the CP-violating NMSSM is described by eighteen independent input parameters which we choose as

$$\begin{aligned}&m_{H_d}^2, m_{H_u}^2, m_S^2,M_W^2, M_Z^2, e, \tan \beta , v_s, \varphi _s, \varphi _u, |\lambda |,\nonumber \\&\quad \varphi _\lambda , |\kappa |, \varphi _\kappa , \text {Re}\,A_{\lambda },\text {Im}\,A_\lambda , \text {Re}\,A_{\kappa }, \text {Im}\,A_\kappa , \end{aligned}$$

(15)

where the three Lagrangian parameters $g_1$, $g_2$ and v have been traded for the three physical observables $M_W$, $M_Z$ and the electric coupling e. In the following, the three soft SUSY-breaking mass parameters $m_{H_d}^2, m_{H_u}^2, m_S^2$ as well as $\text {Im}\,A_\lambda$ and $\text {Im}\,A_\kappa$ will be replaced by the tadpole parameters $t_{\phi _i}$ ($\phi _i=h_d, h_u, h_s, a_d, a_s$)¹. At tree level these tadpoles vanish at the minimum of the Higgs potential. They are, however, non zero at one-loop level, and hence kept for the renormalization procedure. There is also the option to replace the parameter $\text {Re}\,A_{\lambda }$ by the charged Higgs boson mass.

The electroweakino sector The fermionic partners of the neutral Higgs bosons, the neutral higgsinos $\tilde{H}_u$, $\tilde{H}_d$ and the singlino $\tilde{S}$, mix with the neutral gauginos $\tilde{B}$ and $\tilde{W}^3$, resulting in five neutralinos. The mass term of the neutralinos is given in the basis of the Weyl spinor field $\psi ^0=(\tilde{B},\ \tilde{W}^3,\ \tilde{H}_d,\ \tilde{H}_u, \tilde{S})^T$ as

$$\begin{aligned} {\mathcal {L}}^{\psi ^0}_\mathrm{Mass}=\frac{1}{2}(\psi ^0)^TM_N\psi ^0+\mathrm{h.c.}, \end{aligned}$$

(16)

with the $5\times 5$ symmetric mass matrix $M_N$,

$$\begin{aligned} M_N= \begin{pmatrix} M_1 &{} 0&{}-c_\beta M_Z s_{\theta _W}&{} s_\beta M_Z s_{\theta _W} e^{-i \varphi _u}&{} 0 \\ 0 &{} M_2&{}M_W c_{\beta }&{}- s_\beta M_W e^{-i \varphi _u} &{} 0 \\ -c_\beta M_Z s_{\theta _W}&{} M_W c_\beta &{}0&{}\frac{-\lambda v_S e^{i \varphi _s}}{\sqrt{2}}&{} \frac{-\lambda s_\beta ve^{i \varphi _u}}{\sqrt{2}} \\ s_\beta M_Z s_{\theta _W} e^{-i \varphi _u}&{}- s_{\beta }M_W e^{-i \varphi _u} &{}\frac{-\lambda v_S e^{i \varphi _s}}{\sqrt{2}}&{} 0 &{}\frac{-\lambda c_\beta v}{\sqrt{2}}\\ 0&{}0 &{}\frac{-\lambda s_\beta v e^{i \varphi _u}}{\sqrt{2}}&{} \frac{-\lambda c_\beta v}{\sqrt{2}}&{} \sqrt{2}\kappa v_s e^{i \varphi _s}\nonumber \end{pmatrix}.\\ \end{aligned}$$

(17)

By introducing the $5\times 5$ orthogonal matrix N, the mass matrix is diagonalized by performing the rotation²

$$\begin{aligned} \mathrm{diag}(m_{{\tilde{\chi }}^0_1}, m_{{\tilde{\chi }}^0_2}, m_{{\tilde{\chi }}^0_3}, m_{{\tilde{\chi }}^0_4}, m_{{\tilde{\chi }}^0_5})=N^*M_NN^\dagger , \end{aligned}$$

(18)

where the matrix N transforms the fields $\psi ^0_i \equiv (\psi ^0)_i$ into the mass eigenstates $\chi ^0_i \equiv (\chi ^0)_i$ $(i=1,\ldots , 5)$, i.e.,

$$\begin{aligned} \chi ^0=N\psi ^0. \end{aligned}$$

(19)

The neutralino mass eigenstates are given by the Majorana fields ${\tilde{\chi }}^0_i=(\chi ^0_i,\overline{\chi ^0_i})^T$ $(i=1,\ldots ,5)$. By convention, the mass ordering of the ${\tilde{\chi }}^0_i$ is chosen as $m_{{\tilde{\chi }}^0_1}\le \cdots \le m_{{\tilde{\chi }}^0_5}$. We choose $M_1$ and $M_2$ as input parameters, so that the masses $m_{{\tilde{\chi }}^0_i}$ are derived quantities.

Similarly, the charged higgsinos $\tilde{H}^\pm _d$ and $\tilde{H}^\pm _u$ mix with the charged gauginos $\tilde{W}^\pm$ resulting in the charginos. In the basis of the spinors $\psi ^-_R=(\tilde{W}^-, \tilde{H}^-_d)^T,\ \psi ^+_L=(\tilde{W}^+, \tilde{H}^+_u)^T$, built from the Weyl spinors $\tilde{H}_u^\pm$, $\tilde{H}_d^\pm$, $\tilde{W}^\pm$, the chargino mass terms are expressed as

$$\begin{aligned} {\mathcal {L}}_{\mathrm{Mass}}^{\psi _{L/R}}=(\psi _R^-)^TM_C\psi ^+_L+\mathrm{h.c.}, \end{aligned}$$

(20)

with

$$\begin{aligned} M_C= \begin{pmatrix} M_2 &{} \sqrt{2}s_\beta M_We^{-i\varphi _{u}}\\ \sqrt{2}c_\beta M_W &{}\lambda v_s e^{i\varphi _{S}} /\sqrt{2}\\ \end{pmatrix}. \end{aligned}$$

(21)

The spinors $\psi ^+_L,\ \psi ^-_R$ are rotated into the mass eigenstates $\tilde{\chi }^+_L=(\tilde{\chi }^+_{L_1},\tilde{\chi }^+_{L_2})^T,\ \tilde{\chi }^-_R=(\tilde{\chi }^-_{R_1},\tilde{\chi }^-_{R_2})^T$ by

$$\begin{aligned} \tilde{\chi }_L^+=V\psi _L^+,\quad \tilde{\chi }_R^-=U\psi _R^-, \end{aligned}$$

(22)

where U and V are $2\times 2$ unitary matrices. Thereby, the mass matrix for the charginos can be diagonalized as

$$\begin{aligned} \mathrm{diag}(m_{{\tilde{\chi }}_1^{\pm }}, m_{{\tilde{\chi }}_2^{\pm }})=U^*M_C V^\dagger , \end{aligned}$$

(23)

with the charginos described by the Dirac spinors ($i=1,2$)

$$\begin{aligned} {\tilde{\chi }}_i^+ = \left( \begin{array}{c} \tilde{\chi }_{L_i}^+ \\ \overline{\tilde{\chi }_{R_i}^-} \end{array}\right) . \end{aligned}$$

(24)

The convention used for the mass ordering is the same as that for the neutralinos, namely, $m_{{\tilde{\chi }}_1^{\pm }}\le m_{{\tilde{\chi }}_2^{\pm }}$. In total, the electroweakino sector requires four additional input parameters which are the absolute values of the gaugino masses and their corresponding two complex phases, hence

$$\begin{aligned} |M_1| ,|M_2|, \varphi _{M_1},\varphi _{M_2}. \end{aligned}$$

(25)

The Sfermion sector In the sfermion sector, we only consider the third generation which is the relevant one for our calculation of the charged Higgs boson decays. The mass terms for the left-handed and right-handed sfermions are derived from the soft-breaking Lagrangian Eq. (3) as well as from the F- and D-terms of the supersymmetric Lagrangian. This yields the mass matrices for the stops and sbottoms,

$$\begin{aligned} M_{\tilde{t}}&= \begin{pmatrix} m_{\tilde{Q}_3}^2+m_t^2+c_{2\beta }M_Z^2(I_{t}-Q_{t}s_{\theta _W}^2) &{} m_t(A_t^* e^{- i \varphi _u}- \mu _{\mathrm{eff}}/t_\beta )\\ m_t(A_t e^{i \varphi _u}- \mu _{\mathrm{eff}}^{*}/t_\beta ) &{}m_t^2+ m^2_{\tilde{t}_R}+Q_{t}c_{2\beta }M_Z^2s_{\theta _W}^2 \end{pmatrix}, \nonumber \\ M_{\tilde{b}}&= \begin{pmatrix} m_{\tilde{Q}_3}^2+m_b^2+c_{2\beta }M_Z^2(I_{b}-Q_{b}s_{\theta _W}^2) &{} m_b(A_b^*- e^{i \varphi _u}\mu _{\mathrm{eff}}t_\beta )\\ m_b(A_b- e^{-i \varphi _u}\mu _{\mathrm{eff}}^*t_\beta ) &{}m_b^2+ m^2_{\tilde{b}_R}+Q_{b}c_{2\beta }M_Z^2s_{\theta _W}^2 \end{pmatrix}, \end{aligned}$$

(26)

with the isospins $I_{t}$, $I_{b}$ and the electric charges $Q_{t}$, $Q_{b}$ given by $I_{t}=\frac{1}{2}$, $I_{b}=-\frac{1}{2}$, $Q_{t}=\frac{2}{3}$, $Q_{b}=-\frac{1}{3}$, and

$$\begin{aligned} \mu _{\mathrm{eff}}=\frac{\lambda v_s e^{i\varphi _s} }{\sqrt{2}} = \frac{|\lambda | v_s }{\sqrt{2}} e^{i(\varphi _\lambda + \varphi _s)}. \end{aligned}$$

(27)

The mass matrix which mixes left- and right-handed staus reads

$$\begin{aligned} M_{\tilde{\tau }}= \begin{pmatrix} m_{\tilde{L}_3}^2+m_\tau ^2+c_{2\beta }M_Z^2(I_{\tau }-Q_{\tau }s_{\theta _W}^2) &{} m_\tau (A_\tau ^*- e^{i \varphi _u} \mu _{\mathrm{eff}}t_\beta )\\ m_\tau (A_\tau - e^{-i \varphi _u} \mu _{\mathrm{eff}}^*t_\beta ) &{}m_\tau ^2+ m^2_{\tilde{\tau }_R}+Q_{\tau }c_{2\beta }M_Z^2s_{\theta _W}^2\nonumber \end{pmatrix},\\ \end{aligned}$$

(28)

with $Q_{\tau }=-1, I_{\tau }=-1/2$. The sneutrino masses are given by

$$\begin{aligned} m^2_{\tilde{\nu }_i} =\frac{1}{2} M_Z^2 c_{2\beta } + m_{\tilde{L}_i}^2, \end{aligned}$$

(29)

with the generation indices $i=1,2,3$. In our setting, only left-handed neutrinos exist and hence the neutrinos are massless.

Using a $2\times 2$ rotation matrix for the sfermions, $U^{\tilde{f}}$, which relates $\tilde{f}_L$, $\tilde{f}_R$ to the mass eigenstates $\tilde{f}_1$ and $\tilde{f}_2$, we get

$$\begin{aligned} \begin{pmatrix} \tilde{f}_1\\ \tilde{f}_2 \end{pmatrix}= U^{\tilde{f}} \begin{pmatrix} \tilde{f}_L\\ \tilde{f}_R \end{pmatrix}. \end{aligned}$$

(30)

The sfermion mass matrices are diagonalized as $(\tilde{f}=\tilde{t}, \tilde{b},\tilde{\tau })$

$$\begin{aligned} \mathrm{diag}(m_{\tilde{f}_1}^2, m_{\tilde{f}_2}^2)=U^{\tilde{f}}M_{\tilde{f}}U^{\tilde{f}\dagger }. \end{aligned}$$

(31)

In the calculation of the mass matrices $M_{\tilde{t}},M_{\tilde{b}}$ and $M_{\tilde{\tau }}$, the soft SUSY-breaking masses $m_{\tilde{Q}_3}^2$, $m_{\tilde{t}_R}^2$, $m_{\tilde{b}_R}^2$ and the trilinear soft SUSY-breaking couplings $A_t,\ A_b, A_\tau$ are chosen as input parameters, so that the mass eigenvalues are outputs, for which the convention $m_{\tilde{f}_1}\le m_{\tilde{f}_2}$ is used as before.

In addition to the input parameters of the Higgs and electroweakino sectors, we have seven more input parameters for the third generation of the squarks,

$$\begin{aligned} m_t,m_b,m_{\tilde{Q}_3}^2, m_{\tilde{t}_R}^2,m_{\tilde{b}_R}^2,A_t,A_b, \end{aligned}$$

(32)

and four parameters for the third-generation of the sleptons

$$\begin{aligned} m_\tau ,m_{\tilde{L}_3}^2, m_{\tilde{\tau }_R}^2,A_\tau . \end{aligned}$$

(33)

3 Renormalization of the NMSSM

In order to obtain UV-finite results at one-loop level, the renormalization of the parameters and external fields is mandatory. In particular, the bare parameters $p_0$ of the Lagrangian are replaced by the corresponding renormalized parameters, p, and the counterterms, $\delta p$, as

$$\begin{aligned} p_0= p +\delta p \end{aligned}$$

(34)

and the bare fields $\phi _0$ are expressed via the renormalized fields $\phi$ and the wave-function renormalization constants (WFRCs) $Z_\phi$ as

$$\begin{aligned} \phi _0 = \sqrt{Z_\phi }\phi = \left( 1 + \frac{\delta Z_\phi }{2}\right) \phi . \end{aligned}$$

(35)

In our previous studies [45, 47, 50,51,52], we have established the renormalization schemes in the complex NMSSM. We will adopt these procedures for the computation of the NLO corrections to the two-body decays of the charged Higgs bosons and summarize here the main points.

• The complex phases $\varphi _u,\varphi _s,\varphi _\lambda ,\varphi _\kappa , \varphi _{M_1}, \varphi _{M_2}$ do not need to be renormalized at one-loop level, see [45, 50].

• The tadpole counterterms are chosen in such way that the minimum of the Higgs potential does not change at one-loop level, leading to

  $$\begin{aligned} \delta t_{\phi _i} = t_{\phi _i}^{(1)}, \quad \phi _i=h_d, h_u, h_s, a_d, a_s, \end{aligned}$$

  (36)

  where $t_{\phi _i}^{(1)}$ are the tadpole contributions at one-loop level.

• The SM electroweak parameters $e, M_W,M_Z$, inspired by their experimental measurements, are renormalized in the on-shell (OS) scheme. The W and Z mass counterterms are given by

  $$\begin{aligned} \delta M_Z^2 = \text{ Re } \Sigma _{ZZ}^T (M_Z^2), \quad \delta M_W^2 = \text{ Re } \Sigma _{WW}^T (M_W^2), \end{aligned}$$

  (37)

  and the electric charge counterterm reads

  $$\begin{aligned} \delta Z_e= & {} \frac{1}{2} \left. \frac{\partial \Sigma ^T_{\gamma \gamma } (k^2)}{\partial k^2}\right| _{k^2=0} + \frac{s_W}{c_W} \frac{\Sigma ^T_{\gamma Z} (0)}{M_Z^2} - \frac{1}{2}\Delta \alpha (M_Z^2), \,\,\,\qquad \end{aligned}$$

  (38)
  $$\begin{aligned} \Delta \alpha (M_Z^2)= & {} \frac{\partial \Sigma ^{\text {light},T}_{\gamma \gamma }}{\partial k^2}\bigg \vert _{k^2=0}-\frac{ \text{ Re } \Sigma ^{\text {light},T}_{\gamma \gamma }(M_Z^2)}{M_Z^2}, \end{aligned}$$

  (39)

  where $\Sigma _{VV^\prime }^T$, $V,V^\prime =\gamma ,W,Z$, denote the transverse part of the respective self-energies. The notation ’$\text{ Re }$’ means that we take only the real part of the loop integrals. The above definition of the electric charge counterterm has been chosen to avoid the dependence of the results on large logarithms $\ln m_f$ from the light fermion $f\ne t$ contributions [57]. It corresponds to the input of the fine structure constant at the Z boson mass. Therefore, in Eq. (39) the photon self-energy $\Sigma ^{\text {light},T}_{\gamma \gamma }$ includes only the light fermion contributions.

• The charged Higgs mass in the calculation of the NLO decay widths is always renormalized in the OS scheme and its counterterm is defined via the charged Higgs self-energy,

  $$\begin{aligned} \delta M_{H^\pm }^2 = \text{ Re } \Sigma _{H^\pm H^\mp } (M_{H^\pm }^2). \end{aligned}$$

  (40)

  Note that in the computation of the loop-corrected Higgs masses in NMSSMCALCEW if the charged Higgs mass is an input parameter it is renormalized in the OS scheme. In case the ${{\overline{\mathrm{DR}}}}$ parameter $\text{ Re } A_\lambda$ is an input parameter, however, the charged Higgs mass is a derived quantity. The derived value will then be used as input in the decay part as an OS parameter.

• The parameters $|\lambda |,|\kappa |,v_s,\tan \beta$, and Re$A_\kappa$ are renormalized in the ${{\overline{\mathrm{DR}}}}$ scheme. The counterterms for $|\lambda |$ ,$|\kappa |$ and $v_s$ can be defined from the electroweakino sector [50, 56] or from the neutral Higgs boson sector. Both derivations lead to the same results which has been confirmed explicitly by our previous calculations.

• The gaugino mass parameters $|M_1|, |M_2|$ can be renormalized in the OS or the ${{\overline{\mathrm{DR}}}}$ scheme. In Ref. [45] we worked with three possible renormalization schemes which we called OS1, OS2 and ${{\overline{\mathrm{DR}}}}$. In OS1, the OS conditions are imposed on the wino-like chargino and the bino-like neutralino, while in OS2 they are applied to the wino- and the bino-like neutralinos. All three schemes lead to small loop corrections to the masses of the remaining neutralinos and charginos, cf. Ref. [45].

• The renormalization of the squark sector, i.e. of the parameters $m_t,m_b,m_{\tilde{Q}_3}^2, m_{\tilde{t}_R}^2, m_{\tilde{b}_R}^2,A_t,$ and $A_b$ can be performed in the OS or the ${{\overline{\mathrm{DR}}}}$ scheme. In Ref. [45] we provided the counterterms for both schemes and we also presented our evaluation of the one-loop SUSY-QCD and SUSY-EW corrections to the masses of the squarks. We observed large loop corrections to the squark masses and the decay widths of the heavy neutral Higgs bosons into squarks [39, 45]. The counterterms of the slepton sector can be derived similarly to the squark sector and are implemented both for the OS and the ${{\overline{\mathrm{DR}}}}$ scheme.

• The neutral Higgs fields are renormalized in the ${{\overline{\mathrm{DR}}}}$ scheme. The OS property of an external neutral Higgs boson is ensured by using the wave-function renormalization factors (WFRFs) $\mathbf{Z}^{H}$. Thereby potentially large corrections arising from external lines with neutral Higgs bosons can be resummed into the decay widths via WFRFs. The expressions for $\mathbf{Z}^{H}$ can be found in e.g. Ref. [48] for the real NMSSM and Ref. [45] for the complex case.

• The charged Higgs fields are also renormalized in the ${{\overline{\mathrm{DR}}}}$ scheme. Their WFRCs are related to the WFRCs of the neutral Higgs fields as they are in the same doublet [51, 52]. Unlike the neutral Higgs field, we cannot use the resummed WFRFs for external charged Higgs bosons since they contain an infrared (IR) divergence due to the contribution from the massless photon. We therefore expand the charged Higgs WFRFs to take only into account the pure one-loop term which is equivalent to the use of an OS charged Higgs wave function renormalization constant $\delta Z_{H^\pm }$,

  $$\begin{aligned} \delta Z_{H^\pm }&=-\left. \frac{\partial \Sigma _{H^+H^- }}{\partial p^2}\right| _{p^2=M_{{H^\pm }}^2}. \end{aligned}$$

  (41)

• The SM fermionic fields and the neutralino and chargino fields are renormalized in the OS scheme defined at the respective tree-level masses of the fields. The counterterm expressions for the neutralinos and charginos can be found in Ref. [45]. The OS property of the external fermionic line is justified if the corresponding mass of the fermion is also renormalized in the OS scheme. This is the case for the SM fermionic fields. However, in case of the neutralinos and charginos, some or all of them³ cannot be renormalized OS. As mentioned in the sixth point in this list, the loop corrections to the masses of the neutralinos and charginos in the studied renormalization schemes, OS1, OS2 and ${{\overline{\mathrm{DR}}}}$, are small. This allows us to use the OS WFRCs defined at the tree-level masses in the decay processes. In the cases where loop-corrections to particles on the external line are large, i.e squarks, we have to use the modified squark WFRCs which are defined at the loop-corrected masses [45],

  $$\begin{aligned} \delta Z^{\tilde{q}}_{ii}(M_{\tilde{q}_i}^2)= & {} - \frac{\partial \Sigma ^{\tilde{q}\, \text {div}}_{ii}(p^2)}{\partial p^2}\bigg {|}_{p^2 = m_{\tilde{q}_i}^2}\nonumber \\&- \frac{\partial {\hat{\Sigma }}^{\tilde{q}}_{ii}(p^2)}{\partial p^2}\bigg {|}_{p^2 = M_{\tilde{q}_i}^2}, \quad i=1,2 , \end{aligned}$$

  (42)

  for the diagonal WFRCs and

  $$\begin{aligned} \delta Z^{\tilde{q}}_{ij}(M_{\tilde{q}_k}^2)= & {} \frac{\Sigma ^{\tilde{q} \,\text {div}}_{ij}(m_{\tilde{q}_{i}}^2)- \Sigma ^{\tilde{q}\, \text {div}}_{ij}(m_{\tilde{q}_{j}}^2)}{m_{\tilde{q}_{j}}^2 -m_{\tilde{q}_{i}}^2}\nonumber \\&-2 \frac{{\hat{\Sigma }}^{\tilde{q}}_{ij}(M_{\tilde{q}_k}^2)}{M_{\tilde{q}_k}^2- m_{\tilde{q}_i}^2},\quad i,j,k=1,2, \quad i\ne j, \nonumber \\ \end{aligned}$$

  (43)

  for the off-diagonal WFRCs. Here $\Sigma ^{\tilde{q}}_{ij}$ denotes the unrenormalized self-energy for the $\tilde{q}^*_i\rightarrow \tilde{q}^*_j$ transition and the ${\hat{\Sigma }}^{\tilde{q}}$ stands for the renormalized one. The capital letter $M_{\tilde{q}}$ is used for the loop-corrected mass while the small letter $m_{\tilde{q}}$ for the tree-level mass. The superscript ’$\text {div}$’ means that we take only the UV divergent part. $M_{\tilde{q}_k}$ stands for the loop-corrected mass of the external squark where $\tilde{q}_k$ can be either $\tilde{q}_i$ or $\tilde{q}_j$. The renormalization of the slepton fields is performed in the OS scheme in accordance with their mass renormalization.

Given our flexibility in choosing different renormalization schemes, many particles may get loop-corrections to their masses, e.g. Higgs bosons, neutralinos, charginos, squarks, and sleptons. Loop corrections to the Higgs boson masses have been computed at the two-loop order $\mathcal{O}(\alpha _t \alpha _s + \alpha _t^2)$ [51, 52] while for the neutralinos, charginos, squarks and sleptons loop corrections are calculated at one-loop level [45]. These corrections, depending on the chosen renormalization scheme, have been implemented in the code NMSSMCALCEW [45]. We use the loop-corrected masses in the initial and in the final states of the decay processes. However, we use the tree-level masses and tree-level couplings, if not specified otherwise, in the internal lines of the loop diagrams to ensure the cancellation of the UV divergences.

4 Higher-order corrections to the two-body decays of the charged Higgs bosons

In this section we describe the computation of the NLO EW, QCD as well as SUSY-EW, and SUSY-QCD corrections to various two-body decays of the positively charged Higgs boson $H^+$. The NLO corrections for the decay widths of the negatively charged Higgs boson are derived in a similar way. In the real NMSSM the decay widths of the $H^+$ and $H^-$ are the same, however, in the presence CP-violating phases they may not be equal. In the following, we will discuss the decay modes $H^{+}\rightarrow q q^{\prime }$, $H^{+}\rightarrow \ell \nu$, $H^{+}\rightarrow \tilde{\chi }^{+} \tilde{\chi }^{0}$, $H^{+}\rightarrow \tilde{q} \tilde{q}^{\prime }$, and $H^{+}\rightarrow \tilde{\ell } \tilde{\nu }^{\prime }$. The NLO SUSY-EW corrections to Higgs boson decays into neutral Higgs bosons and a $W^+$ boson as well as their gauge dependences have been discussed in Ref. [48]. Higher-order corrections to the two-body decays of the neutral Higgs bosons in the CP-conserving and CP-violating NMSSM have been presented in Refs. [45,46,47].

We used the public codes FeynArts [58, 59], FormCalc [60] and FeynCalc [61, 62] in order to generate the Feynman diagrams and calculate the squared amplitudes. The NMSSM model file for FeynArts has been generated with the help of SARAH [63,64,65,66]. We have performed two independent calculations for all processes studied here and the results are in full agreement.⁴

The UV divergent diagrams are regularized by the dimensional reduction scheme [67] which is equivalent to the constrained differential renormalization scheme [68, 69] at one loop level as was shown in Ref. [60] and preserves SUSY at this level.

4.1 Charged Higgs boson decays into fermions

In our previous implementation in NMSSMCALC, the charged Higgs boson decay width includes higher-order QCD corrections for the quark final states⁵ while the decays into lepton final states were evaluated at tree level. We have taken into account, however, the universal large corrections proportional to $\tan \beta$ that arise from the SUSY-QCD (for the top-bottom final state) and the SUSY-EW (for the top-bottom and the $\tau$-neutrino final states) corrections by absorbing them into effective Yukawa couplings as described in our publication [53]. In this section we improve the calculation of the decay widths by including the missing one-loop SUSY-QCD and SUSY-EW corrections, i.e. their finite remainders. We present here the decay into the third generation fermions. Other decays into the first and second generation are kept as implemented in NMSSMCALC, i.e. apart from the absorption into effective couplings where applicable no further one-loop SUSY-QCD and SUSY-EW corrections have been included, since they are suppressed by the smallness of couplings due to the light quark masses and/or small CKM matrix elements. We note that in the setting of NMSSMCALC the CKM matrix is set to unity in the calculation of the loop corrections. This setting is valid for the third generation since the mixing with the first and second generations is small. We, however, keep the corresponding CKM matrix element in front of the charged Higgs decay widths as a factor and do not renormalize it.

The Yukawa interaction terms of the charged Higgs boson with third generation quarks and leptons read

$$\begin{aligned}&V_{tb} {\bar{t}}\left( g^{L}_{H^+ b{\bar{t}}} P_L + g^{R}_{H^+ b{\bar{t}}} P_R \right) b H^+ \nonumber \\&\quad + {\bar{\nu }}_\tau \left( g^{L} _{H^+ \tau {\bar{\nu }}_\tau } P_L + g^{R}_{H^+ \tau {\bar{\nu }}_\tau } P_R \right) \tau H^+ +\text { h.c.}, \end{aligned}$$

(44)

where the projection operators $P_{L/R}$ are given by $P_{L/R} = (1\mp \gamma _5)/2$ and $V_{tb}$ is the CKM matrix element. The explicit expressions of the tree-level couplings are given by

$$\begin{aligned} g^{R,\mathrm{tree}}_{H^+ b\bar{t}}&=e^{i\frac{\varphi _u}{2}}\frac{\sqrt{2}m_b }{v}\tan \beta ,\nonumber \\ g^{L,\mathrm{tree}}_{H^+ b{\bar{t}}}&=e^{i\frac{\varphi _u}{2}}\frac{\sqrt{2} m_t}{v}\cot \beta , \end{aligned}$$

(45)

$$\begin{aligned} g^{R,\mathrm{tree}}_{H^+ \tau {\bar{\nu }}_\tau }&=\frac{\sqrt{2} m_\tau }{v}\tan \beta ,\nonumber \\ g^{L,\mathrm{tree}}_{H^+ \tau {\bar{\nu }}_\tau }&=0. \end{aligned}$$

(46)

In NMSSMCALC we included higher-order QCD corrections to the decay width $H^+\rightarrow t{\bar{b}}$ based on HDECAY [54, 55, 73]. In HDECAY, there is an interpolation between the decay width that is valid near the threshold $m_t+m_b-\delta<M_{H^\pm }<m_t+m_b+\delta$ ($\delta =2 \,{\text {GeV}}$) and the one that is valid far above the threshold $M_{H^\pm }\ge m_t+m_b+\delta$. We include the newly computed one-loop SUSY-QCD and SUSY-EW corrections in the latter case. Our implemented loop-corrected decay width is hence given by

$$\begin{aligned}&\Gamma [H^+\rightarrow t\bar{b}\,] = \frac{3 G_F M^3_{H^\pm }}{4\sqrt{2}\pi } |V_{tb}|^2 \, \beta ^{1/2}(\mu _t,\mu _b) \, \nonumber \\&\quad \times \left\{ (1-\mu _t -\mu _b) \left[ \frac{\mu _t}{ \tan ^2 \beta } \left( 1+ \frac{4}{3} \frac{\alpha _s}{\pi } \delta _{tb}^+ \right) \right. \right. \nonumber \\&\quad \left. \left. +\mu _b^2 \tan ^2 \beta R^2 \left( 1+ \frac{4}{3} \frac{\alpha _s}{\pi } \delta _{bt}^+ \right) \right] \right. \nonumber \\&\left. \quad -4\mu _t\mu _b R \left( 1+ \frac{4}{3} \frac{\alpha _s}{\pi } \delta _{tb}^- \right) \right\} \nonumber \\&\quad + |V_{tb}|^2 \Gamma _{H^+\rightarrow t\bar{b}}^{\text {SUSYQCD}}+ |V_{tb}|^2 \Gamma _{H^+\rightarrow t\bar{b}}^{\text {SUSYEW}}], \end{aligned}$$

(47)

where $\mu _i = m_i^2/M_{H^\pm }^2$ ($i=t,b$), with $m_{t/b}$ being pole masses and

$$\begin{aligned} \beta ^{1/2}(\mu _t,\mu _b) =(1-\mu _t-\mu _b)^2-4\mu _t\mu _b \end{aligned}$$

(48)

denotes the two-body phase space factor. Explicit expressions for $\delta _{tb}^+,\delta _{bt}^+$ and $\delta _{tb}^-$ can be found in Ref. [73]. The universal SUSY-QCD and SUSY-EW corrections that become large in the large $\tan \beta$ regime are resummed into effective bottom Yukawa couplings. These $\Delta _b$ corrections are incorporated into the decay width through the R factor,

$$\begin{aligned} R = \frac{1}{1+\Delta _b} \left[ 1 - \frac{\Delta _b}{\tan ^2\beta } \right] , \end{aligned}$$

(49)

where the explicit expression for $\Delta _b$ is given by [73,74,75,76,77,78,79,80,81]

$$\begin{aligned} \Delta _b= & {} \frac{\Delta _b^{\text {QCD}}+\Delta _b^{\text {elw}}}{1+\Delta _1}, \end{aligned}$$

(50)

with the one-loop corrections for the complex NMSSM [53]

$$\begin{aligned} \Delta _b^{\text {QCD}}= & {} \frac{C_F}{2} \, \frac{\alpha _s (\mu _R)}{\pi } \, M_3^* \, \mu _{\text{ eff }}^* \, \tan \beta \, I (m_{\tilde{b}_1}^2, m_{\tilde{b}_2}^2 , m_{\tilde{g}}^2 ), \end{aligned}$$

(51)

$$\begin{aligned} \Delta _b^{\text {elw}}= & {} \frac{\alpha _t (\mu _R)}{4\pi } \, A_t^* \, \mu _{\text{ eff }}^* \, \tan \beta \, I (m_{\tilde{t}_1}^2, m_{\tilde{t}_2}^2 , |\mu _{\text{ eff }}|^2), \end{aligned}$$

(52)

$$\begin{aligned} \Delta _1= & {} - \frac{C_F}{2} \, \frac{\alpha _s (\mu _R)}{\pi }\, M_3^*\, A_b \, I (m_{\tilde{b}_1}^2, m_{\tilde{b}_2}^2 , m_{\tilde{g}}^2 ), \end{aligned}$$

(53)

where $\alpha _t = y_t^2/(4\pi )$ with $y_t = \sqrt{2} m_t /(v \sin \beta )$ is the top-Yukawa coupling and $C_F=4/3$. The generic function I is defined as

$$\begin{aligned} I(a,b,c)= & {} \frac{ab \, \log \frac{a}{b} + bc \, \log \frac{b}{c} + ca \, \log \frac{c}{a}}{(a-b)(b-c)(a-c)}. \end{aligned}$$

(54)

The remaining one-loop SUSY-QCD and SUSY-EW corrections are denoted by $\Gamma _{H^+\rightarrow t\bar{b}}^{\text {SUSYQCD}}$ and $\Gamma _{H^+\rightarrow t\bar{b}}^{\text {SUSYEW}}$ in Eq. (47), respectively. The SUSY-EW correction can be expressed as

$$\begin{aligned} \Gamma _{H^+\rightarrow t{\bar{b}}}^{\text {SUSYEW}}&= \frac{3\beta ^{1/2}\left( \mu _t,\mu _b\right) M_{H^\pm }}{8\pi }\nonumber \\&\quad \times \Bigg [ \left( 1-\mu _t-\mu _b\right) \mathrm{Re}\left[ g_{ H^+ b\bar{t}}^{L, \mathrm{tree}}\left( \Delta _{ H^+ b\bar{t}}^{L, \mathrm{SUSYEW}}\right) ^*\right. \nonumber \\&\left. \quad + g_{ H^+ b\bar{t}}^{R, \mathrm{tree}}\left( \Delta _{ H^+ b\bar{t}}^{R, \mathrm{SUSYEW}}\right) ^* \right] \nonumber \\&\quad -2\sqrt{\mu _t\mu _b}\ \mathrm{Re}\left[ {g}_{ H^+ b\bar{t}}^{L,\mathrm tree}\left( \Delta _{ H^+ b\bar{t}}^{R, \mathrm SUSYEW}\right) ^* \right. \nonumber \\&\left. \quad +{g}_{ H^+ b\bar{t}}^{R,\mathrm tree}\left( \Delta _{ H^+b\bar{t}}^{L,\mathrm SUSYEW}\right) ^*\right] \Bigg ]+ \Gamma _{H^+\rightarrow t{\bar{b}} \gamma }, \end{aligned}$$

(55)

where $\Delta _{ H^+ b\bar{t}}^{L/R, \mathrm{SUSYEW}}$ denote the left- and right-handed form factors of the renormalized one-loop amplitude and include the following contributions

$$\begin{aligned} \Delta _{ H^+ b\bar{t}}^{L/R, \mathrm{SUSYEW}}&= \Delta _{ \mathrm SUSYEW}^{L/R, \mathrm{vert}}+\Delta _{\mathrm{SUSYEW}}^{L/R, \mathrm{CT}}\nonumber \\&\quad +\Delta _{ \mathrm SUSYEW}^{L/R, \mathrm{GWmix}}+\Delta _\mathrm{SUSYEW}^{L/R, \mathrm{sub}}. \end{aligned}$$

(56)

The $\Delta _{\mathrm{SUSYEW }}^{L/R, \mathrm{vert}}$ contributions are computed from the corresponding one-loop triangle diagrams.⁶ The counterterm contributions read

$$\begin{aligned} \Delta ^{R, \mathrm{CT}}_{\mathrm{SUSYEW}}&= g^{R, \mathrm{tree}}_{H^+b\bar{t}} \left( \frac{\delta m_b}{m_b}-\frac{\delta v}{v}-\frac{\delta c_\beta }{c_\beta }\right. \nonumber \\&\left. \quad +\frac{1}{2}\delta \bar{Z}_R^t+\frac{1}{2}\delta Z_L^b+\frac{1}{2}\delta Z_{H^\pm }+ \frac{ c_\beta ^3}{ s_\beta } \delta t_\beta \right) , \end{aligned}$$

(57)

$$\begin{aligned} \Delta ^{L, \mathrm{CT}}_{\mathrm{SUSYEW}}&=g^{L, \mathrm{tree}}_{H^+b\bar{t}} \left( \frac{\delta m_t}{m_t}-\frac{\delta v}{v}-\frac{\delta s_\beta }{s_\beta }\right. \nonumber \\&\left. \quad +\frac{1}{2}\delta \bar{Z}_L^t+\frac{1}{2}\delta Z_R^b+\frac{1}{2}\delta Z_{H^\pm } - c_{\beta }s_{\beta } \delta t_\beta \right) , \end{aligned}$$

(58)

where $\delta v$ is given in terms of the counterterms for e, $M_W$ and $M_Z$ as,

$$\begin{aligned} \frac{\delta v}{v} = \frac{\delta e}{e} + \frac{c_W^2}{2s_W^2} \left( \frac{\delta M_Z^2}{M_Z^2} - \frac{\delta M_W^2}{M_W^2} \right) + \frac{\delta M_W^2}{2 M_W^2}. \end{aligned}$$

(59)

The contributions from the transition of the charged Higgs boson on the external line to the charged $W^+$ boson and the charged Goldstone boson, respectively, do not vanish. They are denoted by $\Delta _\mathrm{SUSYEW}^{L/R, \mathrm{GWmix}}$ and given by

$$\begin{aligned} \Delta ^{L, \mathrm{GWmix}}_{\mathrm{SUSYEW}}&=\frac{e m_t e^{i\varphi _u/2}}{\sqrt{2}s_W M_W^2}{\hat{\Sigma }}_{H^+W^+}(M_{H^\pm }^2)\;, \end{aligned}$$

(60)

$$\begin{aligned} \Delta ^{R, \mathrm{GWmix}}_{\mathrm{SUSYEW}}&= -\frac{e m_b e^{i\varphi _u/2}}{\sqrt{2}s_W M_W^2}{\hat{\Sigma }}_{H^+ W^+}(M_{H^\pm }^2), \end{aligned}$$

(61)

where ${\hat{\Sigma }}_{H^+W^+}(M_{H^\pm }^2)$ is the renormalized self-energy of the transition $H^+\rightarrow W^+$ computed at $p^2 = M_{H^\pm }^2$. The last term in Eq. (56) represents the subtraction terms which are needed to avoid double counting arising from the $\Delta _b$ corrections. They read

$$\begin{aligned} \Delta ^{L, \mathrm{sub}}_{\mathrm{SUSYEW}}&=0, \end{aligned}$$

(62)

$$\begin{aligned} \Delta ^{R, \mathrm{sub}}_{\mathrm{SUSYEW}}&= g^{R, \mathrm{tree}}_{H^+b\bar{t}}\frac{\Delta _b^{\mathrm{elw}}}{s_\beta ^2} \;, \end{aligned}$$

(63)

with $\Delta _b^{\mathrm{elw}}$ given in Eq. (52). The contribution from real photon emission, $\Gamma _{H^+\rightarrow t{\bar{b}} \gamma }$ in Eq. (55), is needed to cancel the infrared divergences (IR) from the triangle contributions. The decay width for the real emission of a photon reads

$$\begin{aligned} \Gamma _{H^+\rightarrow t \bar{b}\gamma }&=\frac{\alpha N_C M_{H^\pm }}{36\pi ^2 v^2}\Bigg [ \left( \mu _b t^2_\beta + \frac{\mu _t}{t^2_\beta }\right) \nonumber \\&\quad \times \bigg (-8 I_{21}^{00}+6 I_{01}^{22}-14 I_1^{0}+8 I_1^{2}-17 I_2^{0}-3 I_0^{1}\nonumber \\&\quad -7 I_2^{1}+3 I_ 0^{2}-26 I \bigg ) \nonumber \\&\quad +4M_{H^\pm }^2 \left( (\mu _b+\mu _t-1)\left( \mu _b t^2_\beta + \frac{\mu _t}{t^2_\beta }\right) + 4 \mu _t\mu _b\right) \nonumber \\&\quad \times \bigg (2 \left( M_{H^\pm }^2 -m_t^2 -m_b^2\right) I_{21}\nonumber \\&\quad +6 \left( M_{H^\pm }^2 +m_t^2 -m_b^2\right) I_{01} +3 \left( M_{H^\pm }^2 -m_t^2 +m_b^2\right) I_{02}\nonumber \\&\quad +9 M_{H^\pm }^2 I_{00}+4 m_t^2 I_{11}+m_b^2 I_{22}+9 I_0+4I_1+I_2\bigg ) \Bigg ], \end{aligned}$$

(64)

where we have dropped the arguments $(M_{H^\pm }^2,m_{t}^2,m_{b}^2)$ of the I functions for better readability. In the above formulae, the I functions are the Bremsstrahlung integrals defined as [57]

$$\begin{aligned} I_{i_1...i_n}^{j_1...j_m}&=\frac{1}{\pi ^2}\int \frac{d^3k_1}{2k_1^0}\frac{d^3k_2}{2k_2^0}\frac{d^3k_\gamma }{2k_g^0}\delta ^{(4)}(k_0-k_1-k_2-k_\gamma )\nonumber \\&\quad \times \frac{(\pm 2k_\gamma \cdot k_{j_1})\ .\ .\ . \ (\pm 2k_\gamma \cdot k_{j_m})}{(\pm 2k_\gamma \cdot k_{i_1})\ .\ .\ . \ (\pm 2k_\gamma \cdot k_{i_n})}, \end{aligned}$$

(65)

where $k_{0}$, $k_{1}$ and $k_{2}$ stand for the incoming momentum of the charged Higgs boson and the outgoing momentum of top and bottom quark, respectively, while $k_{\gamma }$ is the outgoing momentum of the photon. For the sign of the momentum products $k_\gamma \cdot k_{i_n}$ and $k_\gamma \cdot k_{j_m}$, the minus sign is chosen only when the indices $i_n, \ j_m$ are 0. In the I functions defined above, the integrals $I_{00},\ I_{01},\ I_{02},\ I_{11},\ I_{22},$ and $I_{12}$ are IR divergent. We checked that the analytical expression Eq. (64) is consistent with the generic result for the real corrections to $S\rightarrow F\bar{F}$ (S denotes a scalar, F a fermion) calculated in Ref. [42].

The SUSY-QCD contribution, $\Gamma _{H^+\rightarrow t\bar{b}}^{\text {SUSYQCD}}$, can be computed in a similar way as the SUSY-EW corrections,

$$\begin{aligned}&\Gamma _{H^+\rightarrow t{\bar{b}}}^{\text {SUSYQCD}} = \frac{3\beta ^{1/2}\left( \mu _t,\mu _b\right) M_{H^\pm }}{8\pi }\nonumber \\&\quad \times \Bigg [ \left( 1-\mu _t-\mu _b\right) \mathrm{Re}\left[ g_{ H^+ b\bar{t}}^{L, \mathrm{tree}}\left( \Delta _{ H^+ b\bar{t}}^{L, \mathrm{SUSYQCD}}\right) ^* \right. \nonumber \\&\quad \left. + g_{ H^+ b\bar{t}}^{R, \mathrm{tree}}\left( \Delta _{ H^+ b\bar{t}}^{R, \mathrm{SUSYQCD}}\right) ^* \right] \nonumber \\&\quad -2\sqrt{\mu _t\mu _b}\ \mathrm{Re}\left[ \tilde{g}_{ H^+ b\bar{t}}^{L,\mathrm tree}\left( \Delta _{ H^+ b\bar{t}}^{R, \mathrm SUSYQCD}\right) ^*\right. \nonumber \\&\left. \quad +\tilde{g}_{ H^+ b\bar{t}}^{R,\mathrm tree}\left( \Delta _{ H^+b\bar{t}}^{L,\mathrm SUSYQCD}\right) ^*\right] \Bigg ], \end{aligned}$$

(66)

where the left- and right-handed form factors of the renormalized vertex $g_{ H^+b\bar{t}}^{L/R,\mathrm SUSYQCD}$ are given by

$$\begin{aligned} \Delta _{ H^+ b\bar{t}}^{L/R, \mathrm{SUSYQCD}} = \Delta _{\mathrm{SUSYQCD}}^{L/R, \mathrm{vert}}+\Delta _{\mathrm{SUSYQCD}}^{L/R, \mathrm{CT}} +\Delta _{\mathrm{SUSYQCD}}^{L/R, \mathrm{sub}}.\nonumber \\ \end{aligned}$$

(67)

The contribution $\Delta _{\mathrm{SUSYQCD}}^{L/R, \mathrm{vert}}$ comes from one-loop diagrams containing a virtual gluino. The counterterm contributions $\Delta _{\mathrm{SUSYQCD}}^{L/R, \mathrm{CT}}$ are given by Eqs. (57) and (58) by setting the counterterms $\delta v, \delta t_\beta , \delta s_\beta , \delta c_\beta , \delta Z_{H^\pm }$ to zero and including in the computation of $\delta m_{b,t}$ and $\delta Z_{L,R}^{t,b}$ instead of the SUSY-EW the SUSY-QCD corrections. The subtraction terms of the SUSY-QCD contributions read

$$\begin{aligned} \Delta ^{L, \mathrm{sub}}_{\mathrm{SUSYQCD}}&=0, \end{aligned}$$

(68)

$$\begin{aligned} \Delta ^{R, \mathrm{sub}}_{\mathrm{SUSYQCD}}&= g^{R, \mathrm{tree}}_{H^+b\bar{t}}\frac{\Delta _b^{\mathrm{QCD}}+\Delta _1}{s_\beta ^2}, \end{aligned}$$

(69)

with $\Delta _b^{\mathrm{QCD}}$ and $\Delta _1$ given in Eqs. (51) and (53), respectively.

The higher-order corrections for the charged Higgs decays into leptons and neutrinos can be expressed in the same way as the decays into quarks, $H^+\rightarrow t{\bar{b}}$. Since the left-handed form factor of the vertex $H^+l{\bar{\nu }}$ vanishes the formula for the NLO width is given by

$$\begin{aligned}&\Gamma _{H^+\rightarrow \nu \bar{\tau }}^{\mathrm{NLO}}= \frac{M_{H^\pm }}{16\pi } \left( 1-\frac{m_\tau ^2}{M_{H^\pm }^2}\right) ^2 \left( |{ {\tilde{g}}}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}}|^2\right. \nonumber \\&\left. \quad +2\mathrm{Re}\left[ {g}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}}\big (\Delta _{R}^{\mathrm{vert}}+\Delta _{R}^{\mathrm{CT}} +\Delta _{R}^{\mathrm{GWmix}}+\Delta _{R}^{\mathrm{sub}}\big )^*\right] \right) \nonumber \\&\quad +\Gamma (H^+\rightarrow \nu \bar{\tau } \gamma ), \end{aligned}$$

(70)

where the effective tree-level coupling resumming the large $\Delta _\tau$ corrections reads

$$\begin{aligned} {\tilde{g}}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}} ={g}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}} \frac{1-\Delta _\tau /t_\beta ^2}{1 +\Delta _\tau }, \end{aligned}$$

(71)

with

$$\begin{aligned} \ \Delta _\tau= & {} \frac{\alpha _1}{4\pi } M_1^* \mu _\mathrm{eff}^* t_\beta I(m_{{\tilde{\tau }}_1}^2,m_{{\tilde{\tau }}_2}^2, |M_1|^2)\nonumber \\&+ \frac{\alpha _2}{4\pi } M_2^* \mu _{\mathrm{eff}}^* t_\beta I(m_{{\tilde{\nu }}_\tau }^2,m_{{\tilde{\tau }}_2}^2, |M_2|^2) \end{aligned}$$

(72)

and

$$\begin{aligned} \alpha _{1,2}= \frac{g_{1,2}^2}{4\pi } . \end{aligned}$$

(73)

The vertex correction $\Delta _{R}^{\mathrm{vert}}$ is given by the corresponding genuine one-loop triangle diagrams. The counterterm contribution, which is needed to cancel the UV divergences arising from the genuine one-loop triangle contribution, is denoted by $\Delta _{R}^{\mathrm{CT}}$ and reads

$$\begin{aligned} \Delta _{R}^{\mathrm{CT}}= & {} {g}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}}\left( \frac{\delta m_\tau }{m_\tau } - \frac{\delta v}{v}- \frac{\delta c_\beta }{c_\beta } \right. \nonumber \\&\left. + \frac{1}{2} \delta Z_{H^\pm } + \frac{c_\beta ^3}{s_\beta }\delta t_\beta +\frac{1}{2} \delta Z_\tau +\frac{1}{2} \delta \bar{Z}_{\nu _\tau } \right) . \end{aligned}$$

(74)

For the one-loop $H^\pm$-W/G mixing contributions $\Delta ^\mathrm{GWmix}_{R}$ to the effective coupling we get

$$\begin{aligned} \Delta _{R}^{\mathrm{GWmix}} =-\frac{ g_{2}m_\tau }{\sqrt{2}}\frac{\hat{\Sigma }_{H^+W^+}}{M_W^2}, \end{aligned}$$

(75)

and the subtraction term to avoid double counting reads

$$\begin{aligned} \Delta _{R}^{\mathrm{sub}} = {g}_{ H^+ \tau \bar{\nu }_\tau }^{R, \mathrm{tree}} \Delta _\tau \left( 1 + \frac{1}{t_\beta ^2}\right) . \end{aligned}$$

(76)

The real photon emission $\Gamma _{H^+\rightarrow \nu \bar{\tau } \gamma }$ can be cast into the form

$$\begin{aligned} \Gamma _{H^+\rightarrow \nu \bar{\tau } \gamma }&=\frac{\alpha t^2_\beta m_\tau ^2}{4 \pi ^2 v^2 M_{H^{\pm }} }\nonumber \\&\quad \times \bigg (-2 (M_{H^{\pm }}^2 -m_\tau ^2 ) \big (M_{H^{\pm }}^2 \left( I_{00}+I_{20}\right) \nonumber \\&\quad +m_\tau ^2 \left( I_{20}+I_{22}\right) +I_0+I_2\big )-I_2^0-I \bigg ), \end{aligned}$$

(77)

where the arguments $(M_{H^{\pm }}^2,0,m_{\tau }^2)$ of the bremsstrahlung functions have been dropped.

4.2 Charged Higgs boson decays into electroweakinos

In this section, we present the results for charged Higgs bosons decaying into a pair of electroweakinos. The Lagrangian describing the interaction between a charged particle $H_k^+$ ($k=1$ for the charged Goldstone boson $G^+$ and $k=2$ for the charged Higgs boson $H^+$) and a neutralino $\tilde{\chi }_i^0$ ($i=1,\ldots ,5$) and a chargino $\tilde{\chi }_j^-$ ($j=1,2$) reads

$$\begin{aligned} {\bar{\psi }}_{\tilde{\chi }_i^0} \left( g^{R}_{H^+_k \tilde{\chi }_i^0\tilde{\chi }^-_j} P_R+g^{L}_{H^+_k \tilde{\chi }_i^0 \tilde{\chi }^-_j }P_L\right) \psi _{\tilde{\chi }_j^-} H^+_k +\text { h.c.}. \end{aligned}$$

(78)

The tree-level couplings are given by

$$\begin{aligned} g_{H^+_k \tilde{\chi }_i^0\tilde{\chi }^-_j}^{R,\mathrm{tree}}&= -\frac{1}{\sqrt{2}}{V}_{j2}\Big ((g_1N_{i1}+g_2N_{i2})Z^{H^\pm }_{k2}e^{i \varphi _u}+\sqrt{2}\lambda ^*N_{i5}Z^{H^\pm }_{k1}\Big )\nonumber \\&\quad -g_2 e^{i \varphi _u} {V}_{j1}N_{i4} Z^{H^\pm }_{k2}, \end{aligned}$$

(79)

$$\begin{aligned} g_{H^+_k \tilde{\chi }_i^0\tilde{\chi }^-_j}^{L,\mathrm{tree}}&= -\frac{1}{\sqrt{2}}{U}_{j2}^*\Big ({-}g_1N_{i1}^*Z^{H^\pm }_{k1} {-}g_2N_{i2}^*Z^{H^\pm }_{k1} +\sqrt{2} e^{i \varphi _u}\lambda N_{i5}^*Z^{H^\pm }_{k2}\Big )\nonumber \\&\quad -g_2{U}_{j1}^*N_{i3}^*Z^{H^\pm }_{k1}, \end{aligned}$$

(80)

with the matrix elements

$$\begin{aligned} Z^{H^\pm }_{11}=-Z^{H^\pm }_{22}=-c_\beta , \quad Z^{H^\pm }_{12}=Z^{H^\pm }_{21}=s_\beta . \end{aligned}$$

(81)

In the previous version of NMSSMCALC, we included only the tree-level decay width which reads

$$\begin{aligned}&\Gamma ^{\mathrm{tree}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^+_j } = \frac{\beta ^{1/2}\left( \mu _i,\mu _j\right) M_{H^\pm }}{16\pi }\nonumber \\&\quad \times \Bigg [ \left( 1-\mu _i-\mu _j \right) \left( |g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L, \mathrm{tree}}|^2+|{g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R, \mathrm{tree}}|^2\right) \nonumber \\&\quad -2 \sqrt{\mu _i\mu _j}\left( {g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L,\mathrm{tree}}(g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R,\mathrm{tree}})^* +{g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R,\mathrm{tree}}(g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L,\mathrm{tree}})^* \right) \Bigg ],\qquad \nonumber \\ \end{aligned}$$

(82)

where $\mu _i = M_{{\tilde{\chi }}_i^0}^2/M_{H^+}^2$ and $\mu _j = M_{{\tilde{\chi }}_j^+}^2/M_{H^+}^2$.⁷ We now include the NLO SUSY-EW corrections to the decay width as

$$\begin{aligned} \Gamma ^{\mathrm{NLO}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^+_j }= \Gamma ^{\mathrm{tree}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^-_j } +\Gamma ^{\mathrm{SUSYEW}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^-_j }, \end{aligned}$$

(83)

with

$$\begin{aligned} \Gamma ^{\mathrm{SUSYEW}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^+_j }= & {} \frac{\beta ^{1/2}\left( \mu _i,\mu _j\right) M_{H^\pm }}{8\pi } \nonumber \\&\times \Bigg [ \left( 1-\mu _i-\mu _j \right) \mathrm{Re}\left[ g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L, \mathrm{tree}}\Delta _{L}^*+{g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R, \mathrm{tree}}\Delta _{R}^*\right] \nonumber \\&-2 \sqrt{\mu _i\mu _j}\ \mathrm{Re}\left[ {g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L,\mathrm{tree}}\Delta _{R}^* +{g}_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R,\mathrm{tree}}\Delta _{L}^* \right] \Bigg ]\nonumber \\&+ \Gamma _{H^+\rightarrow {\tilde{\chi }}_i^0{\tilde{\chi }}^{+}_j\gamma }\,. \end{aligned}$$

(84)

The left- and right-handed form factors $\Delta _{L/R}$ consist of the genuine triangle one-loop diagram contributions $\Delta _{L/R}^\mathrm{vert}$, the counterterms $\Delta _{L/R}^{\mathrm{CT}}$ and the contributions $\Delta _{L/R}^{\mathrm{GWmix}}$ from the transitions of $H^+\rightarrow G^+/W^+$ on the external line,

$$\begin{aligned} \Delta _{L/R}= & {} \Delta _{L/R}^{\mathrm{vert}} + \Delta _{L/R}^{\mathrm{CT}} + \Delta _{L/R}^{\mathrm{GWmix}}. \end{aligned}$$

(85)

The counterterm contributions read

$$\begin{aligned} \Delta _{R}^{\mathrm{CT}}= & {} -\frac{1}{\sqrt{2}}{V}_{j2}\Big ((\delta g_1N_{i1}+ \delta g_2N_{i2})c_\beta e^{i \varphi _u}\nonumber \\&+\sqrt{2}\delta \lambda ^*N_{i5}s_\beta \Big ) - \delta g_2 e^{i \varphi _u} {V}_{j1}N_{i4} c_\beta \nonumber \\&+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_m \tilde{\chi }_i^0\tilde{\chi }^-_j}^{R,\mathrm{tree}}\delta Z^{H^\pm }_{m k} \nonumber \\&+ \frac{1}{2} \sum _{m=1}^5 g_{H^+_k \tilde{\chi }_m^0\tilde{\chi }^-_j}^{R,\mathrm{tree}}\delta {\bar{Z}}^{\tilde{\chi }^0}_{L,im} + \frac{1}{2} \sum _{m=1}^2 g_{H^+_k \tilde{\chi }_i^0\tilde{\chi }^-_m}^{R,\mathrm{tree}}\delta Z^{\tilde{\chi }^+}_{R,mj} \qquad \end{aligned}$$

(86)

$$\begin{aligned} \Delta _{L}^{\mathrm{CT}}= & {} -\frac{1}{\sqrt{2}}{U}_{j2}^*\Big ({-}\delta g_1N_{i1}^*Z^{H^\pm }_{k1} {-}\delta g_2N_{i2}^*Z^{H^\pm }_{k1} \nonumber \\&+\sqrt{2} e^{i \varphi _u}\delta \lambda N_{i5}^*Z^{H^\pm }_{k2}\Big ) -\delta g_2{U}_{j1}^*N_{i3}^*Z^{H^\pm }_{k1}\nonumber \\&+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_m \tilde{\chi }_i^0\tilde{\chi }^-_j}^{L,\mathrm{tree}}\delta Z^{H^\pm }_{m k} + \frac{1}{2} \sum _{m=1}^5 g_{H^+_k \tilde{\chi }_m^0\tilde{\chi }^-_j}^{L,\mathrm{tree}}\delta {\bar{Z}}^{\tilde{\chi }^0}_{R,im} \nonumber \\&+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_k \tilde{\chi }_i^0\tilde{\chi }^-_m}^{L,\mathrm{tree}}\delta Z^{\tilde{\chi }^+}_{L,mj}. \end{aligned}$$

(87)

The $\Delta _{L/R}^{\mathrm{GWmix}}$ can be expressed in terms of the renormalized self-energy ${\hat{\Sigma }}_{H^+W^+}(M_{H^\pm }^2)$ as

$$\begin{aligned} \Delta _{L}^{\mathrm{GWmix}}= & {} \left( M_{\tilde{\chi }^+_j} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^L- M_{\tilde{\chi }^0_i} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^R\right) \frac{{\hat{\Sigma }}_{H^+W^+}(M_{H^\pm }^2)}{M_W^2},\nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} \Delta _{R}^{\mathrm{GWmix}}= & {} \left( M_{\tilde{\chi }^+_j} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^R- M_{\tilde{\chi }^0_i} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^L\right) \frac{{\hat{\Sigma }}_{H^+W^+}(M_{H^\pm }^2)}{M_W^2},\qquad \nonumber \\ \end{aligned}$$

(89)

where

$$\begin{aligned} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^R= & {} g_2\left( {V}_{j1} N^*_{i2} - {V}_{j2} N^*_{i4}/\sqrt{2}\right) , \end{aligned}$$

(90)

$$\begin{aligned} g_{W^+\tilde{\chi }_i^0\tilde{\chi }_j^-}^L= & {} g_2 \left( {U}_{j1}^* N_{i2} + {U}_{j2}^* N_{i3}/\sqrt{2}\right) . \end{aligned}$$

(91)

The IR divergences which appear in the $\Delta _{L/R}^{\mathrm{vert}}$ vertex corrections are removed by the contribution from the real photon emission. It is given by

$$\begin{aligned} \Gamma _{H^+\rightarrow {\tilde{\chi }}_i^0{\tilde{\chi }}^{+}_j\gamma }&=\frac{2\alpha \Gamma ^{\mathrm{tree}}_{H^+ \rightarrow \tilde{\chi }_i^0\tilde{\chi }^-_j }}{\pi \beta ^{1/2}\left( \mu _i,\mu _j\right) }\nonumber \\&\quad \times \bigg [ -2 \left( M_{H^\pm }^2 I_{00}+I_{01} (M_{H^\pm }^2+M_{\tilde{\chi }_{i}^{-}}^2-M_{\tilde{\chi }_{i}^{0}}^2 )\right. \nonumber \\&\quad \left. +M_{\tilde{\chi }_{i}^{-}}^2 I_{11} +I_0 +I_1 \right) \bigg ] +\frac{\alpha }{8\pi ^2 M_{H^\pm } }\left( g_{H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j}^{R, \mathrm{tree}} \right. \nonumber \\&\quad \times \left. (g_{H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L, \mathrm{tree}})^* + g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{L, \mathrm{tree}} (g_{ H^+ {\tilde{\chi }}_i^0 {\tilde{\chi }}^{-}_j }^{R, \mathrm{tree}})^* \right) \left( I_1^{0}+I\right) , \end{aligned}$$

(92)

where the arguments $(M_{{H^\pm }}^2,M_{\tilde{\chi }_{j}^{+}}^2,M_{\tilde{\chi }_{i}^{0}}^2)$ of the I functions have been dropped.

4.3 Charged Higgs decays into squarks and sleptons

In this section, we give the expressions for the loop-corrected decays of the charged Higgs boson into squarks and sleptons. The Lagrangian describing the interactions between the charged particle $H^+_{k}$ (with $H_1 = G^+$ and $H_2 = H^+$) and the squarks and sleptons reads

$$\begin{aligned} i g_{H^+_k \tilde{t}^*_i\tilde{b}_j} H^+_k \tilde{t}^*_i\tilde{b}_j + i g_{H^+_k \tilde{\nu }_\tau \tilde{\tau }_i^*} H^+_k \tilde{\nu }_\tau \tilde{\tau }_i +\text { h.c.}, \end{aligned}$$

(93)

with $i,j=1,2$ and the tree-level couplings

$$\begin{aligned} g_{H^+_k \tilde{t}^*_i\tilde{b}_j }= & {} \sum _{a=1}^2\sum _{b=1}^2 U^{\tilde{b}*}_{ja}(C_{H^+_k\tilde{b}\tilde{t}^*})_{ab}(U^{\tilde{t}})_{ib}, \end{aligned}$$

(94)

$$\begin{aligned} g_{H^+_k \tilde{\nu }_\tau \tilde{\tau }_i^* }= & {} -\frac{v U^{\tilde{\tau }*}_{i1} \left( c_{\beta } \left( g_2^2-2 y_{\tau }^2\right) Z^{H^\pm }_{k1}+g_2^2 s_{\beta } \ Z^{H^\pm }_{k2}\right) }{2 \sqrt{2}}\nonumber \\&+U^{\tilde{\tau }*}_{i2} y_{\tau } \left( A_{\tau }^* Z^{H^\pm }_{k1}+e^{i \varphi _u } \ \mu _{\mathrm{eff}} Z^{H^\pm }_{k2}\right) , \end{aligned}$$

(95)

with

$$\begin{aligned} (C_{H^+_k\tilde{b}\tilde{t}^*})_{11}&=-\frac{c_{\beta } v \left( g_2^2-2 y_b^2\right) Z^{H^\pm }_{k1}}{2 \sqrt{2}}-\frac{s_{\beta } v \left( g_2^2-2 y_t^2\right) Z^{H^\pm }_{k2}}{2 \sqrt{2}}, \end{aligned}$$

(96)

$$\begin{aligned} (C_{H^+_k\tilde{b}\tilde{t}^*})_{12}&= e^{i\varphi _u} y_t A_t Z^{H^\pm }_{k2}+\mu _{\mathrm{eff}}^* y_t Z^{H^\pm }_{k1}, \end{aligned}$$

(97)

$$\begin{aligned} (C_{H^+_k\tilde{b}\tilde{t}^*})_{21}&= y_b A_b^* Z^{H^\pm }_{k1}+e^{i \varphi _u } \mu _{\mathrm{eff}} y_b Z^{H^\pm }_{k2}, \end{aligned}$$

(98)

$$\begin{aligned} (C_{H^+_k\tilde{b}\tilde{t}^*})_{22}&=\frac{c_{\beta } e^{i\varphi _u} v y_b y_t Z^{H^\pm }_{k2}}{\sqrt{2}}+\frac{e^{i\varphi _u} s_{\beta } v y_b y_t Z^{H^\pm }_{k1}}{\sqrt{2}}. \end{aligned}$$

(99)

The fermion Yukawa couplings are defined as

$$\begin{aligned} y_t= \frac{\sqrt{2} m_t}{v s_\beta } \quad \text{ and } \quad y_{b/\tau }= \frac{\sqrt{2} m_{b/\tau }}{v c_\beta } . \end{aligned}$$

(100)

The NLO decay width for the process $H^+\rightarrow \tilde{t}_i \tilde{b}_j^*$ consists of the tree-level decay width and the NLO SUSY-QCD⁸ and SUSY-EW corrections,

$$\begin{aligned} \Gamma ^{\mathrm{NLO}}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}= \Gamma ^\mathrm{tree}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}+ \Gamma ^{\mathrm{SUSYQCD}}_{H^+\rightarrow \tilde{t}_i\tilde{b}_j^* }+ \Gamma ^{\mathrm{SUSYEW}}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}\,, \end{aligned}$$

(101)

where the tree-level decay width was implemented in the NMSSMCALC as

$$\begin{aligned} \Gamma ^{\mathrm{tree}}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}= & {} 3R_2|g_{H^+_k \tilde{t}^*_i\tilde{b}_j }| ^2, \end{aligned}$$

(102)

with the two-body phase space factor $R_2=\beta ^{\frac{1}{2}}\left( \mu _i,\mu _j\right) /(16\pi M_{H^\pm })$, $\mu _i= M_{\tilde{t}_i}^2/M_{H^\pm }^2$, $\mu _j= M_{\tilde{b}_j}^2/M_{H^\pm }^2$. The newly computed NLO SUSY-QCD and SUSY-EW corrections are given by

$$\begin{aligned} \Gamma ^{\mathrm{SUSYQCD}}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}= & {} 6R_2g_{H^+_k \tilde{t}^*_i\tilde{b}_j } \Delta ^{\mathrm{SUSYQCD}}_{H^+_k \tilde{t}_i^*\tilde{b}_j } +\Gamma _{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*g}\,, \end{aligned}$$

(103)

$$\begin{aligned} \Gamma ^{\mathrm{SUSYEW}}_{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*}= & {} 6R_2g_{H^+_k \tilde{t}_i^*\tilde{b}_j }\Delta ^{\mathrm{SUSYEW}}_{H^+_k \tilde{t}^*_i\tilde{b}_j } +\Gamma _{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*\gamma }. \end{aligned}$$

(104)

The $\Delta ^{\mathrm{SUSYQCD/SUSYEW}}_{H^+_k \tilde{t}^*_i\tilde{b}_j }$ can be decomposed into

$$\begin{aligned} \Delta ^{\mathrm{SUSYQCD}}_{H^+_k \tilde{t}^*_i\tilde{b}_j }= & {} \Delta _\mathrm{SUSYQCD}^{\mathrm{vert}} + \Delta _{\mathrm{SUSYQCD}}^{\mathrm{CT}} \,, \end{aligned}$$

(105)

$$\begin{aligned} \Delta ^{\mathrm{SUSYEW}}_{H^+_k \tilde{t}^*_i\tilde{b}_j }= & {} \Delta _\mathrm{SUSYEW}^{\mathrm{vert}} + \Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}} + \Delta _{\mathrm{SUSYEW}}^{\mathrm{GWmix}}\,. \end{aligned}$$

(106)

The contributions to $\Delta _{\mathrm{SUSYQCD}}^{\mathrm{vert}}$ ($\Delta _{\mathrm{SUSYEW}}^{\mathrm{vert}}$) arise from one-loop triangle diagrams containing at least a gluon or a gluino (all possible particles except for gluons and gluinos). The SUSY-EW counterterm contribution can be expressed as

$$\begin{aligned} \Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}}= & {} \sum _{a=1}^2\sum _{b=1}^2 U^{\tilde{b}*}_{ja}(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{ab}(U^{\tilde{t}})_{ib}\nonumber \\&+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_m \tilde{t}^*_i\tilde{b}_j }^{\mathrm{tree}}\delta Z^{H^\pm }_{2m}+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_2 \tilde{t}^*_m\tilde{b}_j }^\mathrm{tree}\delta {\bar{Z}}^{\tilde{t}}_{im} \nonumber \\&+ \frac{1}{2} \sum _{m=1}^2 g_{H^+_2 \tilde{t}^*_i\tilde{b}_m }^{\mathrm{tree}}\delta Z^{\tilde{b}}_{jm}, \end{aligned}$$

(107)

where the $(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{ab}$ are obtained from Eqs. (96)–(99) by differentiating these expressions with respect to their parameters except for the rotation matrix $Z^{H^\pm }$, resulting in

$$\begin{aligned}&(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{11}=\frac{c_{\beta }^2 \delta t_{\beta } v \left( s_{\beta }^2 \left( g_2^2-2 y_b^2\right) -c_{\beta }^2 \left( g_2^2-2 y_t^2\right) \right) }{2 \sqrt{2}}\nonumber \\&\quad +\frac{c_{\beta } s_{\beta } \left( 2 v (\delta y_b y_b+\delta y_t y_t-\delta g_2 g_2)+\delta v \left( y_b^2+y_t^2-g_2^2\right) \right) }{\sqrt{2}} \;, \end{aligned}$$

(108)

$$\begin{aligned}&(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{12}=c_{\beta } \delta A_t e^{i\varphi _u} y_t\nonumber \\&\quad +\delta \mu _{\mathrm{eff}}^* s_{\beta } y_t+\delta y_t \left( A_t c_{\beta } e^{i\varphi _u}+\mu _{\mathrm{eff}}^* s_{\beta }\right) , \end{aligned}$$

(109)

$$\begin{aligned}&(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{21}= c_{\beta } \delta \mu _{\mathrm{eff}} e^{i \varphi _u } y_b+\delta A_b^* s_{\beta } y_b\nonumber \\&\quad +\delta y_b \left( A_b^* s_{\beta }+c_{\beta } e^{i \varphi _u } \mu _{\mathrm{eff}} \right) , \end{aligned}$$

(110)

$$\begin{aligned}&(\delta C_{H^+_2\tilde{b}\tilde{t}^*})_{22}=\frac{\delta v e^{i\varphi _u} y_b y_t }{\sqrt{2}}+\frac{\delta y_b e^{i\varphi _u} v y_t }{\sqrt{2}}+\frac{\delta y_t e^{i \varphi _u} v y_b }{\sqrt{2}}, \end{aligned}$$

(111)

with

$$\begin{aligned} \frac{\delta \mu _{\mathrm{eff}}}{\mu _{\mathrm{eff}}}=\frac{\delta \lambda }{\lambda }+\frac{\delta v_s}{v_s}. \end{aligned}$$

(112)

The SUSY-QCD counterterm $\Delta _{\mathrm{SUSYQCD}}^{\mathrm{CT}}$ is similar to the counterterm $\Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}}$, with the modification that the counterterms $\delta g_2$, $\delta v$, $\delta t_\beta$, $\delta \mu _{\mathrm{eff}}$ do not receive QCD contributions and are hence set to zero then, and the remaining counterterms are obtained from SUSY-QCD loop corrections instead of SUSY-EW corrections. The mixing contributions with a $W^+$ boson and a charged Goldstone boson are given by

$$\begin{aligned} \Delta ^{\mathrm{GWmix}}_{\mathrm{SUSYEW}} =\frac{g_2\hat{\Sigma }_{H^{+}W^{+}}(M_{H{\pm }}^{2}) }{\sqrt{2} M_{W}^{2}} \big (M_{ \tilde{t}_{i}}^{2}- M_{ \tilde{b}_{j}}^{2}\big ) U^{\tilde{t}}_{i1} U^{{\tilde{b}}*}_{j1}\,. \end{aligned}$$

(113)

Finally the real photon and gluon emission contributions, necessary to cancel the IR divergences arising from the vertex corrections, are given by

$$\begin{aligned} \Gamma _{H^+\rightarrow \tilde{t}_i \tilde{b}_j^*\gamma }&= \frac{3\alpha }{4\pi ^2 M_{H^{\pm }} }|g_{H^+_k \tilde{t}^*_i\tilde{b}_j }^{\mathrm{tree}}|^2\nonumber \\&\quad \bigg [-\frac{2}{3} (M_{H^{\pm }}^2 +M_{\tilde{t}_i}^2-M_{\tilde{b}_j}^2)I_{10}\nonumber \\&\quad +\frac{1}{3} (-M_{H^{\pm }}^2+M_{\tilde{t}_i}^2-M_{\tilde{b}_j}^2)I_{20}\nonumber \\&\quad -\frac{2}{9} (M_{H^{\pm }}^2-M_{\tilde{t}_i}^2-M_{\tilde{b}_j}^2)I_{21}- M_{H^{\pm }}^2 I_{00}\nonumber \\&\quad -\frac{4}{9} M_{\tilde{t}_i}^2 I_{11}-\frac{1}{9} M_{\tilde{b}_j}^2 I_{22}-I_0-\frac{4}{9} I_1-\frac{1}{9} I_2\bigg ], \end{aligned}$$

(114)

$$\begin{aligned} \Gamma _{H^+\rightarrow \tilde{t}_i\tilde{b}_j^*g}&= \frac{3C_F\alpha _{\mathrm{S}}}{4\pi ^2M_{H^{\pm }}}|g_{H^+_k \tilde{t}^*_i\tilde{b}_j }^{\mathrm{tree}}|^2\Big ((M_{H^{\pm }}^2-M_{\tilde{t}_i}^2-M_{\tilde{b}_j}^2)I_{12}\nonumber \\&\quad -M_{\tilde{b}_j}^2I_{22}-M_{\tilde{t}_i}^2I_{11} -I_1-I_2\Big ), \end{aligned}$$

(115)

where the arguments $(M_{H^{\pm }}^2,M_{\tilde{t}_i}^2,M_{\tilde{b}_j}^2)$ of the I functions have been dropped. The full expressions for the real photon and gluon emission contributions Eqs. (114) and (115) are in agreement with those of Ref. [42].

The NLO decay width for the decay $H^{+}\rightarrow \tilde{\tau }^*_i \tilde{\nu }$ ($i=1,2$) is composed of the tree-level contribution and the SUSY-EW corrections and given by

$$\begin{aligned} \Gamma ^{\mathrm{NLO}}_{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau }= \Gamma ^{\mathrm{tree}}_{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau }+ \Gamma ^{\mathrm{SUSYEW}}_{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau }, \end{aligned}$$

(116)

with the tree-level decay width

$$\begin{aligned} \Gamma ^{\mathrm{tree}}_{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau }= & {} R_2|g_{H^+_{2} \tilde{\nu }_\tau \tilde{\tau }_i^* }| ^2, \end{aligned}$$

(117)

in terms of the coupling $g_{H^+_{2} \tilde{\nu }_\tau \tilde{\tau }_i^* }$ given in Eq. (95) and where in the phase space factor $R_{2}$ the loop-corrected masses of the staus and the sneutrino are used, hence, $\mu _{i}=M^{2}_{\tilde{\tau }_{i}}/M_{H^+}^{2},\ \mu _{j}=M^{2}_{\tilde{\nu }_\tau }/M_{H^+}^{2}$. The NLO SUSY-EW corrections are given by

$$\begin{aligned} \Gamma ^{\mathrm{SUSYEW}}_{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau }= & {} 2R_2g_{H^+_{2} \tilde{\nu }_{\tau } \tilde{\tau }_i^* }^{\mathrm{tree}} \Delta ^{\mathrm{SUSYEW}}_{H^+ \tilde{\nu }_\tau \tilde{\tau }_i^* } +\Gamma _{H^+\rightarrow \tilde{\tau }_i^*\tilde{\nu }_\tau \gamma }, \end{aligned}$$

(118)

where the $\Delta ^{\mathrm{SUSYEW}}_{H^+ \tilde{\nu }_\tau \tilde{\tau }_i^* }$ are given by

$$\begin{aligned} \Delta ^{\mathrm{SUSYEW}}_{H^+ \tilde{\nu }_\tau \tilde{\tau }_i^* } = \Delta _{\mathrm{SUSYEW}}^{\mathrm{vert}} + \Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}} + \Delta _{\mathrm{SUSYEW}}^{\mathrm{GWmix}} \;. \end{aligned}$$

(119)

While $\Delta _{\mathrm{SUSYEW}}^{\mathrm{vert}}$ denotes the contributions from the one-loop triangle diagrams of the loop-corrected decay $H^{+}\rightarrow \tilde{\tau }^{*}_i \tilde{\nu }_{\tau }$, the counterterm contribution $\Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}}$ reads

$$\begin{aligned} \Delta _{\mathrm{SUSYEW}}^{\mathrm{CT}}= & {} \sum _{a=1}^2 U^{\tilde{\tau *}}_{ia}(\delta C_{H^+\tilde{\nu }\tilde{\tau }^* })_{a} + \frac{1}{2} \sum _{m=1}^2 g_{H^+_m \tilde{\nu }_{\tau } \tilde{\tau }_{i}^* }\delta Z^{H^\pm }_{2m}\nonumber \\&+ \frac{1}{2} g_{H^+_2 \tilde{\nu }_{\tau } \tilde{\tau }_{i}^* }\delta {\bar{Z}}^{\tilde{\nu }_{\tau }} + \frac{1}{2} \sum _{m=1}^2 g_{H^+_2 \tilde{\nu }_{\tau } \tilde{\tau }_{m}^* }\delta Z^{\tilde{\tau }}_{im}, \end{aligned}$$

(120)

where

$$\begin{aligned} (\delta C_{H^+\tilde{\tau }^*\tilde{\nu }_{\tau } })_{1}&=\frac{c_{\beta }^2 \delta t_{\beta } v \left( s_{\beta }^2 \left( g_2^2-2 y_\tau ^2\right) -c_{\beta }^2 g_2^2\right) }{2 \sqrt{2}}\nonumber \\&\quad +\frac{c_{\beta } s_{\beta } \left( 2 v (\delta y_\tau y_\tau -\delta g_2 g_2)+\delta v \left( y_\tau ^2-g_2^2\right) \right) }{\sqrt{2}} , \end{aligned}$$

(121)

$$\begin{aligned} (\delta C_{H^+\tilde{\tau }^*\tilde{\nu }_{\tau }})_{2}&={c_{\beta } \delta \mu _{\mathrm{eff}} e^{i \varphi _u } y_\tau }+\delta A_\tau ^* s_{\beta } y_\tau \nonumber \\&\quad +\delta y_\tau \left( A_\tau ^* s_{\beta }+{c_{\beta } e^{i \varphi _u } \mu _{\mathrm{eff}} }\right) . \end{aligned}$$

(122)

The contribution of the G/W mixing reads

$$\begin{aligned} \Delta _{\mathrm{SUSYEW}}^{\mathrm{GWmix}}&=\frac{g_2U^{\tilde{\tau }*}_{i1} \hat{\Sigma }_{H^{+}W^{+}}(M_{H^+}^{2})}{M_W^2\sqrt{2}}(M^{2}_{\tilde{\nu }_{\tau }}-M^{2}_{\tilde{\tau }_{i}}), \end{aligned}$$

(123)

and the real photon emission is given by

$$\begin{aligned} \Gamma _{H^+\rightarrow \tilde{\tau }^*_i \tilde{\nu }_\tau \gamma }&= \frac{\alpha }{4\pi ^2 M_{H^{\pm }}}\bigg ( (-M_{H^{\pm }}^2-M^{2}_{\tilde{\tau }_{i}}+M^{2}_{\tilde{\nu }_{\tau }})I_{01}\nonumber \\&\quad -M_{H^{\pm }}^2 I_{00}-M^{2}_{\tilde{\tau }_{i}} I_{11}-I_0-I_1 \bigg ), \end{aligned}$$

where again the arguments $(M_{H^{\pm }}^2,M^{2}_{\tilde{\tau }_{i}},M^{2}_{\tilde{\nu }_{\tau }})$ of the I functions have been dropped.

5 Numerical results

In the following we will discuss the impact of the computed higher-order corrections on the charged Higgs boson decays and branching ratios. In order to get an overall picture we performed a scan in the NMSSM parameter space and only retained those data sets whose phenomenology is in accordance with the most recent experimental results. For this purpose, the parameter points were checked against compatibility with the experimental constraints from the Higgs data by using the programs HiggsBounds [82,83,84] and HiggsSignals [85]. The effective couplings of the Higgs bosons normalized to the corresponding SM values, that are required as input for these programs, have been obtained with the Fortran code NMSSMCALCEW [45]. One of the neutral CP-even Higgs bosons is identified with the SM-like Higgs boson and will be called h from now on. Its mass is required to lie in the range

$$\begin{aligned} 123 \text{ GeV } \le m_h \le 127 \text{ GeV }. \end{aligned}$$

(124)

The SM input parameters have been chosen as [86, 87]

$$\begin{aligned} \alpha (M_Z)= & {} 1/127.955, \nonumber \\ \alpha ^{\overline{\text{ MS }}}_s(M_Z)= & {} 0.1181, \nonumber \\ M_Z= & {} 91.1876~\mathrm{GeV}, \nonumber \\ M_W= & {} 80.379~\mathrm{GeV} ,\nonumber \\ m_t= & {} 172.74~\mathrm{GeV}, \nonumber \\ m^{\overline{\text{ MS }}}_b(m_b^{\overline{\text{ MS }}})= & {} 4.18~\mathrm{GeV},\nonumber \\ m_c= & {} 1.274~\mathrm{GeV}, \nonumber \\ m_s= & {} 95.0~\mathrm{MeV},\nonumber \\ m_u= & {} 2.2~\mathrm{MeV}, \nonumber \\ m_d= & {} 4.7~\mathrm{MeV}, \nonumber \\ m_\tau= & {} 1.77682~\mathrm{GeV}, \nonumber \\ m_\mu= & {} 105.6584~\mathrm{MeV}, \nonumber \\ m_e= & {} 510.9989~\mathrm{KeV}, \nonumber \\ G_F= & {} 1.16637 \cdot 10^{-5}~\mathrm{GeV}^{-2}. \end{aligned}$$

(125)

For the NMSSM sector we follow the SUSY Les Houches accord (SLHA) format [88] in which the soft SUSY breaking masses and trilinear couplings are understood as ${{\overline{\mathrm{DR}}}}$ parameters at the scale

$$\begin{aligned} \mu _R = M_s= \sqrt{m_{\tilde{Q}_3} m_{\tilde{t}_R}}. \end{aligned}$$

(126)

This is also the renormalization scale that we use in the computation of the higher-order corrections. The code NMSSMCALCEW provides the option to choose either $A_\lambda$ or $M_{H^\pm }$ as input parameter. We adopted the latter choice and used the charged Higgs boson mass as an OS input parameter. The computation of the $\mathcal{O}(\alpha _t\alpha _s +\alpha _t^2)$ corrections to the Higgs boson masses is done in the ${{\overline{\mathrm{DR}}}}$ renormalization scheme of the top/stop sector [51, 52]. In Table 1 we summarize the ranges applied in the parameter scans. In order to ensure perturbativity we apply the rough constraint

$$\begin{aligned} \lambda ^2 + \kappa ^2 < 0.7^2. \end{aligned}$$

(127)

The bottom trilinear coupling has been fixed to

$$\begin{aligned} \quad A_b= 2 \text{ TeV }. \end{aligned}$$

(128)

The mass parameters of the first and second generation sfermions are chosen as

$$\begin{aligned} m_{\tilde{u}_R,\tilde{c}_R} = m_{\tilde{d}_R,\tilde{s}_R} = m_{\tilde{Q}_{1,2}}= m_{{\tilde{L}}_{1,2}} =m_{\tilde{e}_R,{\tilde{\mu }}_R} = 3\;\text{ TeV }.\nonumber \\ \end{aligned}$$

(129)

Table 1 Input parameters for the NMSSM scan. All parameters have been varied independently between the given minimum and maximum values

From the scan we retain those points that have a $\chi ^2$ computed by HiggsSignals-2.2.3 that is consistent with an SM $\chi ^2$ within $2\sigma$.⁹ For the scan and the results presented in the first part of the numerical analysis we keep the CP-violating phases equal to zero. In the second part we turn on various CP-violating phases in order to study their impact individually. Note that in all our CP-conserving scenarios it is the lightest CP-even Higgs boson $H_1$ that is SM-like and has a mass around 125 GeV.

Fig. 1

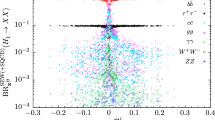
Branching ratios of the charged Higgs boson $H^+$ into various final states including the NLO corrections as described in the text as a function of $M_{H^\pm }$ for all scan parameter points passing the constraints. Left: $t\bar{b}$ (gray diamond), ${\tilde{\chi }}_2^+ {\tilde{\chi }}^0$ (violet diamond), $\tau ^+ \nu _\tau$ (pink circle), $\tilde{t}\tilde{b}^*$ (black diamond), $\mu ^+ \nu _\mu$ (red circle); right: $W^+H$ (orange circle) ${\tilde{\chi }}_1^+ {\tilde{\chi }}^0$ (cyan diamond), ${\tilde{\tau }}^* {\tilde{\nu }}_\tau$ (blue diamond), $c{\bar{s}}$ (green circle)

All the branching ratios shown in the following have been calculated by implementing the higher-order corrections to the various charged Higgs boson decay widths in NMSSMCALCEW. In this way the newly computed corrections are combined with the state-of-the-art higher-order QCD corrections already included in NMSSMCALCEW. Note, however, that the (SUSY-)EW and SUSY-QCD corrections are only taken into account if the respective decay is kinematically allowed. Otherwise, the corresponding decay width without the higher-order corrections discussed in this paper, which only apply for on-shell decays, is used in the computation of the total decay width and branching ratios.

For the computation of radiative corrections we used the following renormalization schemes unless stated differently (see also Sect. 3): In the electroweakino sector we used the OS1 renormalization scheme. For the SUSY-EW corrections to the decays into stop-sbottom and stau-sneutrino pairs the $\overline{\text{ DR }}$ scheme was applied for the stop, sbottom sector and the OS scheme for the stau sector. For details on the definition of the schemes, we refer to Ref. [45].

5.1 The branching ratios

In Fig. 1 we show as function of the charged Higgs boson mass the NLO branching ratios of the charged Higgs boson decays into the various possible final states, namely into the SM-like final states $t\bar{b}$, $\tau ^+ \nu _\tau$, $\mu ^+ \nu _\mu$ and $c\bar{s}$, and the new physics final states $W^+H$, ${\tilde{\chi }}^+_1 {\tilde{\chi }}^0$, ${\tilde{\chi }}^+_2 {\tilde{\chi }}^0$, $\tilde{t}\tilde{b}^*$ and ${\tilde{\tau }}^*{\tilde{\nu }}_\tau$. In the decays into a charged $W^+$ boson plus Higgs final state we have summed up all $W^+H_i$ final states, so that the branching ratio $\text{ BR }(H^+ \rightarrow W^+ H)$ is given by¹⁰

$$\begin{aligned}&\text{ BR }(H^+ \rightarrow W^+ H) \equiv \sum _{i=1}^{3} \text{ BR }(H^+ \rightarrow W^+ H_i) \nonumber \\&\quad + \sum _{j=1}^{2} \text{ BR }(H^+ \rightarrow W^+ A_j). \end{aligned}$$

(130)

Analogously, in the branching ratios into the electroweakino final states we have summed over the neutralinos, hence

$$\begin{aligned} \text{ BR }(H^+ \rightarrow {\tilde{\chi }}^+_{1,2} {\tilde{\chi }}^0) \equiv \sum _{i=1}^5 \text{ BR }(H^+ \rightarrow {\tilde{\chi }}^+_{1,2} {\tilde{\chi }}^0_i) \;. \end{aligned}$$

(131)

Also the decays into the sfermion final states are summed over so that

$$\begin{aligned} \text{ BR }(H^+ \rightarrow \tilde{t}\tilde{b}^*)&\equiv \sum _{i=1}^2 \sum _{j=1}^2 \text{ BR }(H^+ \rightarrow \tilde{t}_i \tilde{b}_j^*), \end{aligned}$$

(132)

$$\begin{aligned} \text{ BR }(H^+ \rightarrow {\tilde{\tau }}^*{\tilde{\nu }}_\tau )&\equiv \sum _{i=1}^2 \text{ BR }(H^+ \rightarrow {\tilde{\tau }}_i^* {\tilde{\nu }}_{\tau }). \end{aligned}$$

(133)

The NLO branching ratios include the higher-order corrections to the Higgs decays widths as presented in the draft, namely the SUSY-EW corrections as well as the QCD and SUSY-QCD corrections for the coloured final states. More specifically, the formulae for the loop-corrected decay widths are given in Eq. (47) for the decay in the top-bottom final state, in Eq. (70) for the decay into $\tau ^+ \nu _\tau$, in Eqs. (83) for the decays into electroweakino pairs, in Eqs. (101) for the decays into stop-sbottom pairs, and in Eq. (116) for those into stau-sneutrino pairs. The implemented higher-order corrections to the decays into charged $W^+$ boson plus Higgs final states have been described in Ref. [48] for the CP-even Higgs bosons in the CP-conserving NMSSM. We have extended this to the CP-violating case. The decays into the SM-like final states include the higher-order QCD and resummed SUSY corrections as specified in the manual for HDECAY [54, 55] and extended to the NMSSM case in [53]. As mentioned above the SUSY-EW and SUSY-QCD corrections are only included in on-shell decays. Otherwise, (where applicable) only QCD corrections and resummed corrections through effective couplings are included. We furthermore include in the decays with on-shell neutral Higgs bosons in the external states the resummed $\mathbf{Z}^{H}$ factors, cf. Sect. 3.

As can be inferred from the plots, the largest branching ratios are given by the decays into top-bottom final states (gray circles) with values of up to almost 100% for charged Higgs mass values below $2\,{\text {TeV}}$. For larger values of the charged Higgs mass the decays into electroweakinos become dominant. For $M_{{H^\pm }}< 1.2\,{\text {TeV}}$, the decays into a charged W plus a neutral Higgs boson provide the second largest branching ratio for some parameter points. As stated above we show here the sum over all possible neutral Higgs bosons. The resulting branching ratio, indicated by the orange circles, can reach up to 98%. The decays into the electroweakinos (cyan diamonds for ${\tilde{\chi }}_1^+ {\tilde{\chi }}^0$, violet diamonds for ${\tilde{\chi }}_2^+ {\tilde{\chi }}^0$) can reach up to 54% (55%) for ${\tilde{\chi }}_1^+ {\tilde{\chi }}^0$ (${\tilde{\chi }}_2^+ {\tilde{\chi }}^0$) when summed up. The summed-up branching ratios into stau-sneutrino pairs (blue diamonds) can go up to 17% for charged Higgs masses below 1.4 TeV and specific parameter configurations, whereas the decays into stop-sbottom pairs (black diamonds) become important for large charged Higgs masses and can have branching ratios of up to 29% in their sum. The branching ratios into $\tau ^+ \nu _\tau$ (pink circles) reach 20%. The branching ratios into $\mu ^+ \nu _\mu$ (red circles) and $c\bar{s}$ (green circles) attain at most $7\cdot 10^{-2}$% and $4 \cdot 10^{-2}$%, respectively. The comparison of these scatter plots with the corresponding ones for the leading order (LO) branching ratios shows that the overall pattern of the distribution of the branching ratios does not change when NLO corrections are included. For individual parameter points the changes can be substantial, however. In the following, we will discuss the impact of the higher-order corrections for the various final states separately.

5.2 Impact of higher-order corrections

For the discussion of the impact of the NLO corrections on the decay width of the decay $H^+ \rightarrow X Y$ we introduce the relative correction of the partial width as

$$\begin{aligned} \delta _{\Gamma }(H^{+}X Y)&=\frac{\Gamma (H^{+}\rightarrow X Y)^\mathrm{NLO} }{\Gamma (H^{+}\rightarrow X Y)^{\mathrm{LO}} }-1 . \end{aligned}$$

(134)

We furthermore define the relative change in the branching ratio for the decay $H^+ \rightarrow X Y$ as

$$\begin{aligned} \Delta _{\mathrm{BR}}^{\mathrm{}}(H^{+}X Y)=\frac{\mathrm{BR}^{\mathrm{NLO}} (H^{+}\rightarrow X Y) -\mathrm{BR}^{\mathrm{LO}}(H^{+}\rightarrow X Y)}{ \mathrm{max}( \mathrm{BR}^{\mathrm{NLO}} (H^{+} \rightarrow X Y),\mathrm{BR}^{\mathrm{LO}}(H^{+} \rightarrow X Y) ) }. \end{aligned}$$

(135)

This quantity allows us to directly identify large corrections in the branching ratios that are not ’artificially’ enhanced because of tiny LO branching ratios.

We have to specify what we mean by LO widths and branching ratios. They are the LO quantities calculated with ’Higgs effective tree-level couplings’, which means that the Higgs tree-level rotation matrix elements have been replaced by the loop-corrected ones. For decays with neutral Higgs bosons in the final state, additionally the improved resummed $\mathbf{Z}^{H}$ factor as described in Ref. [45] is included in the LO decay widths and branching ratios. Note, that these ’LO’ quantities also include the QCD corrections and resummed SUSY-EW and SUSY-QCD corrections in effective quark couplings as already implemented in the first release of NMSSMCALC [53] and described there. In fact the use of the word ’LO’ in essence means that we thereby refer to the old implementation in NMSSMCALC without the genuine SUSY-EW and SUSY-QCD vertex corrections. This means that the definitions Eqs. (134) and (135) give us information on the effects of the newly computed corrections, namely the SUSY-EW and SUSY-QCD vertex corrections, respectively their finite remainders, compared to the previous implementation in NMSSMCALC which only uses the improved LO decay widths as defined here.

5.3 Decays into fermion pairs

Figure 2 displays the relative, $\Delta _\mathrm{BR}$, due to the impact of the SUSY-QCD and SUSY-EW corrections on the branching ratio $\mathrm{BR} (H^+ \rightarrow t\bar{b})$ (left) and the impact of the SUSY-EW corrections on $\mathrm{BR} (H^+ \rightarrow \tau ^+ \nu _\tau )$ (right) as a function of their respective NLO branching ratios. The color code indicates the respective relative corrections to the partial width in per cent for the newly computed SUSY-QCD and SUSY-EW corrections. It shows that the impact of the corrections on the partial width for the decay into $t\bar{b}$ is of moderate size, ranging between $-20$ to $+2$% with a few outliers going down to $-29$%. The relative change in the branching ratio is of similar size with values between $-20$ and $+8$% and a few outliers going down to about $-30$%. Splitting up the contributions, we find that apart from a few outliers the relative SUSY-EW corrections to the partial width (branching ratio) lie between $-16$ and $-2\% (-12\%$ and $+6\%)$, whereas the relative SUSY-QCD corrections range between $-11$ and $+7\% (-10\%$ and $+4\%)$. The SUSY-EW corrections on the width are negative and of comparable size as the SUSY-QCD ones which underlies the importance of including both types of corrections. Large relative corrections to the decay widths of up to about $-30\%$ arise from the sum of SUSY-QCD and SUSY-EW corrections with same sign. The dominant contributions to both the SUSY-EW corrections and the SUSY-QCD corrections stem from one-particle irreducible triangle diagrams. The SUSY-EW corrections to the decay width into $\tau ^+ \nu _\tau$ mostly lie between $-17$ and $+7\%$ and between $-10$ and $+15\%$ for $\Delta _{\mathrm{BR}}$ for the bulk of the points.

Fig. 2

Relative change in the branching ratio as defined in Eq. (135) for the $H^+$ decays into $t\bar{b}$ (left) and and $\tau ^+ \nu _\tau$ (right) as a function of the respective NLO-corrected (SUSY-QCD and SUSY-EW for the former and SUSY-EW for the latter decay) branching ratio for all scan parameter points passing the constraints. The color code indicates the relative correction in the partial width as defined in Eq. (134)

5.4 Decays into gauge plus Higgs boson pairs

In Fig. 3 we show the relative change in the branching ratios due to our newly computed genuine SUSY-EW corrections and as colour code the relative correction for the partial decay widths of the $H^+$ decays into charged $W^+$ boson plus Higgs final states as a function of the corresponding NLO branching ratio. We do not classify the Higgs final states by the mass eigenstates but by the gauge eigenstates, i.e. we show final states with mostly $h_u$, $h_s$ and $a_s$ final states (decays into $W^+ h_d$ and $W^+ a_d$ are kinematically closed). Mostly j-like ($j=h_u,h_s,a_s$) means that the mixing matrix element squared $|R_{i j}|^2$ of the Higgs eigenstate $H_i$ exceeds 0.5. Note, that the $h_u$-like state corresponds to the SM-like Higgs boson as compatibility with the Higgs data requires a maximum coupling to the top-quark.

Fig. 3

Relative change in the branching ratio as defined in Eq. (135) for the $H^+$ decays into $W^+h_u,$ $W^+h_s$, and $W^+a_s$ (going clockwise from upper left to lower middle) as a function of the respective SUSY-EW corrected branching ratio for all scan parameter points passing the constraints. The color code indicates the relative correction in the partial width as defined in Eq. (134)

As can be inferred from the upper left plot the bulk of the corrections to the branching ratio (decay width) for the decay into an $h_u$-like, i.e. SM-like, Higgs boson together with the charged $W^+$ boson lies between $-42$ and $+10\% (-35\%$ and $+3\%$). There are a few outliers with somewhat larger corrections. We note that the branching ratio into $W^+ h_u$ always remains below $0.75 \%$ and is hence rather unimportant for charged Higgs decays.

The branching ratios into singlet-like CP-even Higgs final states, $W^+ h_s$, with up to 25% reach larger values than those into $W^+h_u$. The relative corrections to the decay widths are moderate and range between $-18$ and $+4\%$ with the change in the branching ratio being between $-14$ and $+10\%$. There are two outliers with $\Delta _{\mathrm{BR}}$ reaching up to $-20\%$. Similarly, the corrections to the decay width in the CP-odd singlet-like Higgs state are moderate with corrections to the decay width between $-10$ and $+15\%$ and to the branching ratio between mostly $-2\%$ and $+20\%$. A few outliers can reach corrections to the branching ratio of up to $-23\%$.

Note that for all scattering plots here we do not consider branching ratios that are smaller than $10^{-4}$, since they are not phenomenologically interesting. We can have large relative corrections in these cases because of the suppression of the tree-level couplings.

5.5 Decays into electroweakinos

We now turn to the impact of the SUSY-EW corrections on the decays into electroweakino pairs. The relative changes in the branching ratios and the relative corrections of the decay widths are shown for the final states in the gauge basis, in Fig. 4 for the charged wino and in Fig. 5 for the charged higgsino final state, respectively, together with a neutral electroweakino as specified in the figure labels. In the plots we show results for the parameter points passing our constraints after applying the following cuts: We cut the ratio

$$\begin{aligned} r = \frac{g_2(U_{i2}^* N_{j2}^*-U_{i1}^* N_{j3}^*)}{g_1 U_{i2}^* N_{j1}^*} \end{aligned}$$

(136)

to lie in the range

$$\begin{aligned} 0.5 \le r \le 1.5. \end{aligned}$$

(137)

This ensures that there are no large hierarchies among the left-handed couplings¹¹ of the charged Higgs to a neutralino-chargino pair, cf. Eq. (80), which would otherwise blow up the NLO corrections compared to the LO width. If $r\in [0.5 \cdots 1.5]$, there exist cancellations in the tree-level couplings of the decay in question, that lead to a suppression of the tree-level decay width. Contributions coming from a neutralino close in mass with an enhanced tree-level coupling will dominate and can be very large. In NMSSMCALCEW we print out a warning if this case occurs. Furthermore, for the charged Higgs decay $H^+ \rightarrow {\tilde{\chi }}_i^+ {\tilde{\chi }}_j^0$ we impose the following cuts on the mass differences

$$\begin{aligned}&m_{{\tilde{\chi }}_2^+} - m_{{\tilde{\chi }}_1^+}> 10 \text{ GeV } \, \text{ and } \nonumber \\&m_{{\tilde{\chi }}_{j+1}^0} - m_{{\tilde{\chi }}_{j}^0}> 10 \text{ GeV } \; \wedge \;\; m_{{\tilde{\chi }}_j^0} - m_{{\tilde{\chi }}_{j-1}^0}> 10 \text{ GeV } \,\, \text{ if } \,\,j=2,3,4\nonumber \\&m_{{\tilde{\chi }}_{j+1}^0} - m_{{\tilde{\chi }}_{j}^0}> 10 \text{ GeV } \quad \text{ if } j=1\nonumber \\&m_{{\tilde{\chi }}_j^0} - m_{{\tilde{\chi }}_{j-1}^0} > 10 \text{ GeV } \quad \text{ if } j=5 \end{aligned}$$

(138)

to avoid large mixing effects between the close-in-mass electroweakino masses that also induce huge NLO corrections. Since we use the OS scheme for the WFR constants of the electroweakinos, if two neutralinos (charginos) are degenerate then the WFR constant contributions are dominant and huge.¹² In the code we print out a warning if degenerate cases are involved. In our study, we fix the renormalization scheme for all points to be OS thus encountering about one hundred points¹³ the corrections have the typical size of EW corrections that we comment on in the following. In case of unnaturally large loop corrections we recommend to change the renormalization scheme.

Fig. 4

Relative change in the branching ratio as defined in Eq. (135) for the $H^+$ decay into into charged wino plus neutral electroweakino final states all in the gauge basis as a function of the respective SUSY-EW corrected branching ratio for all scan parameter points passing the constraints. The color code indicates the relative correction in the partial width as defined in Eq. (134)

The maximum relative corrections do not differ much for the charged wino and charged Higgsino final states when comparing the final states with the same neutral electroweakino. The smallest corrections are found for neutral down-type Higgsino production together with a charged wino or Higgsino, i.e. $\tilde{W}^+ \tilde{H}_d^0$ and $\tilde{H}_u^+ \tilde{H}_d^0$. The relative corrections of the partial width lie between about $-16\%$ and $+24\%$ for the former and $-37\%$ and $+2\%$ for the latter, for the bulk of the points. A few outliers involve also corrections of up to $-55\%$ to the $\tilde{H}_u^+ \tilde{H}_d^0$ decay. The relative corrections of the branching ratios lie between about $-4\%$ and $+20\%$ for $\tilde{W}^+ \tilde{H}_d^0$ production and $-30\%$ and 0% for $\tilde{H}_u^+ \tilde{H}_d^0$ production (again for the bulk of the points). The corrections to the $\tilde{W}^+ \tilde{H}_u^0$, $\tilde{W}^+ \tilde{W}^3$, $\tilde{W}^+ \tilde{S}$, $\tilde{H}_u^+ \tilde{H}_u^0$, $\tilde{H}_u^+ \tilde{W}^3$, $\tilde{H}_u^+ \tilde{S}$ final states are somewhat larger but do not exceed what is in general expected for EW corrections. The relative corrections to the decay widths lie between about $-35\%$ and $+40\%$ (depending on the specific final state) for the bulk of the parameter points, and those to the branching ratios between about $-30\%$ and $+30\%$ apart from a few outliers. The largest corrections are found for $\tilde{W}^+ \tilde{B}$, $\tilde{H}_u^+ \tilde{B}$ production where the relative corrections to the partial widths range between $-34\%$ ($-34\%$) and $+77\%$ ($+57\%$) for $\tilde{W}^+ \tilde{B}$ ($\tilde{H}_u^+ \tilde{B}$) and to the branching ratios between $-30$ and $+40\%$ barring a few outliers that can go up to $-100\%$. These are found, however, for small LO widths and branching ratios so that the relative correction easily gets enhanced.

Let us also briefly comment on the size of the branching ratios. The largest branching ratios are obtained for the $\tilde{H}_u^+ \tilde{W}^3$ and $\tilde{W}^+ \tilde{W}^3$ final states with 37% and 30%, respectively, followed by $\tilde{H}_u^+ \tilde{B}$ (35%) and $\tilde{W}^+ \tilde{B}$ (25%) production. The branching ratios into $\tilde{W}^+ \tilde{H}_d^0$, $\tilde{W}^+ \tilde{H}_u^0$, $\tilde{W}^+ \tilde{S}$, $\tilde{H}_u^+ \tilde{H}_u^0$, $\tilde{H}_u^+ \tilde{S}$ reach maximum values between 10 and 20%. The smallest branching ratio is found for the $\tilde{H}_u^+ \tilde{H}_d^0$ final state with at most 0.5%.

Fig. 5

Same as Fig. 4 but for the charged Higgsino plus neutral electroweakino final states

5.6 Decays into Sfermions

Fig. 6

Relative change in the branching ratio as defined in Eq. (135) for the $H^+$ decays into stop-sbottom (left) and stau-sneutrino (right) as a function of their NLO corrected branching ratio for all scan parameter points passing the constraints. The color code indicates the relative corrections in the partial width as defined in Eq. (134)

Like for the electroweakino decays also in the decays into sfermions we apply some cuts to get rid of artificially enhanced corrections due to specific corners in the parameter space. Thus we require for the decays into stop-sbottom pairs, $H^+ \tilde{t}_i \tilde{b}_j$, that the involved masses fulfill

$$\begin{aligned} M_{H^+} - M_{\tilde{t}_i} - M_{\tilde{b}_j} > 40 \text{ GeV } \end{aligned}$$

(139)

so that large corrections originating from threshold effects in triangle loop diagrams do not play a role. Furthermore, we apply the following cuts on the mass differences¹⁴

$$\begin{aligned}&|M_{\tilde{t}_i}-m_{\tilde{t}_{i'}}|> 10 \text{ GeV }\quad \text{ and } \nonumber \\&|M_{\tilde{b}_j}-m_{\tilde{b}_{j'}}| > 10 \text{ GeV } \quad \text{ with }\,\, i\ne i', \; j \ne j' . \end{aligned}$$

(140)

This way large corrections arising from degenerate squark mixing contributions are removed. In case of large loop corrections, we recommend the user to change the renormalization scheme of the stop/sbottom sector as in the case of decays into electroweakinos.

The relative corrections to the decay widths and branching ratios into sfermion final states are shown in Fig. 6 for the stop-sbottom final state on the left and for the stau-sneutrino final state on the right. Note that we sum over all possible final states $\tilde{t}_i \tilde{b}_j^*$ ($i,j=1,2$) in the left and ${\tilde{\tau }}_{i}^*{\tilde{\nu }}_\tau$ ($i=1,2$) in the right plot. The reason why we have less points in the stop-sbottom than in the stau-sneutrino case is simply because in a lot of the scenarios of our scan compatible with the applied constraints the former decays are kinematically closed.

The decays into squarks receive SUSY-EW and SUSY-QCD corrections. For most of the points the relative SUSY-QCD corrections to the decay widths are distributed between 10 and 90%, while the typical size for the SUSY-EW corrections is between $-30$ and $+22\%$. The combination of both corrections alters the decay width between $-37$ and $+92\%$. Some parameter points can reach corrections of up to more than 100% which is due to the renormalization of the squark wave functions in the SUSY-QCD corrections and calls for future improvements through the inclusion of higher-order corrections or resummation. Barring these outliers the relative corrections in the branching ratios range between $-10$ and $+50\%$.

The relative corrections to the decays into stau-sneutrino, stemming only from SUSY-EW corrections, lie between $-64$ and $+72\%$, ranging for the bulk of the corrections only between $-31$ and $+39\%$, however. For $\Delta _{\text {BR}}$ we find values between $-25$ and 30%.

5.7 The impact of CP violation

In contrast to the MSSM, the NMSSM features CP violation in the Higgs sector already at tree level. The NMSSM tree-level Higgs sector contains several complex parameters, as listed in Eq. (15). These CP-violating effects, along with those in the electroweakino and the sfermion sectors, can alter the predictions for the Higgs boson decays compared to the CP-conserving case. The measurement of CP violation at the LHC is a highly non-trivial task requiring the inclusion of as many observables as possible to derive limits on possibly small CP-violating phases. Therefore – in case of discovery – the investigation of CP violation both in the neutral and the charged Higgs sector will be mandatory for the successful determination of CP-violating effects. In [45], we studied the effect of CP violation on the NLO corrections for the neutral Higgs boson decays. Here, we investigate the behaviour of our newly computed NLO corrections to the charged Higgs boson decays for varying complex parameters. We focus on the impact of CP violation in the NLO corrections themselves and therefore vary the CP-violating phases for illustrative purposes over a wide range without taking into account the constraints from the EDMs, namely the strict constraint from the electron EDM provided by the ACME collaboration [36]. For a phenomenological investigation they have to be taken into account, however. Both NMSSMCALC and NMSSMCALCEW allow to compute the EDMs [37] which will be required in this case.

For the investigation of the impact of CP violation on the higher-order corrections to the charged Higgs decays we chose the following parameter point from the set of valid scenarios obtained in our scan,

$$\begin{aligned} M_{H^\pm }= & {} 2537\ \mathrm{GeV}, \; t_\beta =4.84, \; |\lambda |=0.590, |\kappa |=0.339, \nonumber \\ |M_1|= & {} 764 \ \mathrm{GeV}, |M_2|= 917 \ \mathrm{GeV}, \; |M_3|=2211 \ \mathrm{GeV}, \nonumber \\ |A_t|= & {} 3.4\ \mathrm{TeV}, \; |A_b|= 2\ \mathrm{TeV}, \; |A_\tau |= 2\ \mathrm{TeV}, \nonumber \\ |\mu _{\mathrm{eff}}|= & {} 585\ \mathrm{GeV}, \; \text {Re}\,A_\kappa =- 16.4\ \mathrm{GeV}, \; m_{\tilde{Q_{3}}}=1.14\ \mathrm{TeV}, \nonumber \\ m_{\tilde{t}_R}= & {} 1.57\ \mathrm{TeV}, \; m_{\tilde{b}_R}=1.76\ \mathrm{TeV}, \; m_{\tilde{L}_3}=476\ \mathrm{GeV}, \\ m_{{\tilde{\tau }}_R}= & {} 1.66\ \mathrm{TeV.} \end{aligned}$$

The remaining parameters and phases are fixed as

$$\begin{aligned} m_{\tilde{u}_R,\tilde{c}_R}&=m_{\tilde{d}_R,\tilde{s}_R}=m_{\tilde{Q}_{1,2}}=m_{\tilde{L}_{1,2}}=m_{\tilde{e}_R,{\tilde{\mu }}_R}=3\ \mathrm{TeV}, \nonumber \\ \varphi _{M_{1},M_{2},M_{3}}&=\varphi _{A_{t},A_{b},A_{\tau }}=\varphi _{\mu }=\varphi _{\kappa }=0 \;, \end{aligned}$$

(141)

where for simplicity we choose the notation $\varphi _{\mu _\mathrm{eff}}\equiv \varphi _{\mu }$. The lightest CP-even Higgs boson $H_1$ is the SM-like Higgs boson and the Higgs mass spectrum is given by

$$\begin{aligned} M_{H_1}= & {} 123.97 \text{ GeV }, \; M_{H_2}= 132.57 \text{ GeV }, \nonumber \\ M_{H_3}= & {} 680.45 \text{ GeV }, \nonumber \\ M_{A_1}= & {} 2536.92 \text{ GeV }, \; M_{A_2}= 2538.66 \text{ GeV }. \end{aligned}$$

(142)

In the following we vary the three phases $\varphi _{\mu }$, $\varphi _{M_{2}}$, $\varphi _{A_{t}}$ individually away from their benchmark value zero while keeping all the other phases fixed to zero in order to quantify the effect induced by CP violation through the respective non-zero phase. For the phase of $\lambda$, we set $\varphi _{\lambda }=2\varphi _{\mu }/3$ so that we do not encounter CP violation at tree level in the Higgs sector. Note, that we vary the phases almost up to their maximum values leading to scenarios that are already excluded by the EDM constraints. For illustrative purposes, we still allow for these variations, however. We stop all plots at $\pm 0.47\pi$ and not at $\pm \pi /2$ because for phases $|\varphi _\mu | > 0.47\pi$ the singlet-like Higgs boson has a negative mass.

Fig. 7

Left: $\Gamma (H^+\rightarrow t\bar{b})$, right: $\Gamma (H^+\rightarrow W^+H_1)$ as function of the CP-violating phase for $\mu _{\mathrm{eff}}$ (red), $A_{t}$ (blue) and $M_{2}$ (green), respectively. Full lines correspond to the decay width at NLO, while dashed lines are those at LO. The lower panels show the relative corrections $\delta _\Gamma$ as defined in Eq. (134)

In Fig. 7 (left) we show the tree-level and loop-corrected decay width of the charged Higgs decay into the top-bottom final state as function of a variation of either $\varphi _\mu$ (red), $\varphi _{A_t}$ (blue) or $\varphi _{M_2}$ (green) while keeping all other phases to zero and ensuring a vanishing tree-level CP-violating phase in the Higgs sector. The lower panels show the relative corrections of the partial decay width as defined in Eq. (134) as a function of the respective non-zero phase. Despite the vanishing CP-violating phase at tree level we still see a small dependence of the tree-level decay width on the CP-violating phase $\varphi _\mu$ and $\varphi _{A_t}$, respectively. This is due to the $\Delta _b$ corrections included in our definition of the tree-level decay width into quarks, which depends on the phases of $\mu _{\text {eff}}$ and $A_t$. As for the loop corrections, the relative correction which is $\delta _\Gamma = -19\%$ for the chosen parameter point, barely changes when $\varphi _{M_2}$ is turned on, whereas for non-zero $\varphi _\mu$ it varies from -19% to $-11$% for $\varphi _{\mu }=-0.47\pi$ and $-12.5$% for $\varphi _{\mu }=+0.47\pi$. The dependence on $\varphi _{A_t}$ is given by values ranging from $-19\%$ at vanishing phase to $-14$% at $\varphi _{A_t}=\pm 0.47\pi$.

For the decays into a charged $W^+$ plus Higgs boson final state for the chosen benchmark point we see the largest impact of the CP-violating phases on the $W^+H_1$ final state, where $H_1$ is the SM-like Higgs boson, cf. Fig. 7 (right). For $\varphi _\mu$ and $\varphi _{A_t}$ each, the relative corrections vary from about $-10\%$ to at $-0.47\pi$ to about $40\%$ at $+0.47\pi$. The dependence on $\varphi _{M_2}$ is very weak, however. The LO dependence on $\varphi _\mu$ and $\varphi _{A_{t}}$ is due to the inclusion of the two-loop corrections into the final state Higgs boson masses, where the dependence on $\varphi _\mu$ is largest. For the $W^+H_2$ final state $\varphi _{\mu }$ and $\varphi _{M_2}$ change $\delta _\Gamma$ from 3% at zero phase to 4.5% (1% for $\varphi _{\mu }$ and 1.5% for $\varphi _{M_{2}}$) at $0.47\pi$ ($-0.47\pi$). The dependence on $\varphi _{A_t}$ is very small. The loop corrections to $H^+ \rightarrow W^+A_1$ show a smaller dependence on $\varphi _\mu$, $\varphi _{M_2}$ and again the dependence on $\varphi _{A_t}$ is almost negligible. The other decays into charged $W^+$ boson plus Higgs final states are kinematically closed.

The charged Higgs couplings to the electroweakinos depend on the phases $\varphi _\mu$ and $\varphi _{M_2}$ so that the LO decay widths already show a dependence on these CP-violating phases. We exemplary show the effect on the decay $H^+ \rightarrow {\tilde{\chi }}_1^+ {\tilde{\chi }}_2^0$ in Fig. 8 (left). In this case the ${\tilde{\chi }}_1^+$ is a higgsino-like chargino while the ${\tilde{\chi }}_2^0$ is a higgsino-like neutralino. (The CP-violating impact is found to be less important for the ${\tilde{\chi }}_1^+ {\tilde{\chi }}_1^0/{\tilde{\chi }}_3^0$ final states of this benchmark point.) The relative correction $\delta _\Gamma$ shows a substantial dependence on all three phases.

Fig. 8

Left: $\Gamma (H^+\rightarrow \chi ^{+}_{1} \chi ^{0}_{2})$, right: $\Gamma (H^+\rightarrow \tilde{t}_1 \tilde{b}_1^*)$ as a function of $\varphi _\mu$ (red), $\varphi _{A_{t}}$ (blue) and $\varphi _{M_{2}}$ (green) at LO (dashed) and NLO (full). Lower insert: relative correction of the decay width $\delta _\Gamma$

The tree-level charged Higgs couplings to squarks depend on the phases $\varphi _\mu$ and $\varphi _{A_t}$ so that the LO width shows a substantial dependence on these phases that is also translated to NLO, as can be inferred from Fig. 8 (right), which shows the decay $H^+ \rightarrow \tilde{t}_1 \tilde{b}_1^*$ as a function of the CP-violating phases at LO and NLO. (The decays into other stop-sbottom final states are kinematically closed.) The dependence on $\varphi _{M_2}$ is only radiatively induced and very weak.

5.8 The impact of the renormalization scheme

We now want to discuss the impact of the renormalization scheme. The renormalization scheme dependence of the decay widths also gives us a possibility to roughly estimate the remaining theoretical uncertainty due to missing higher-order corrections. The code NMSSMCALCEW that we use for the computation of the decay widths and branching ratios follows the SLHA conventions where the soft SUSY breaking parameters are understood to be $\overline{\text{ DR }}$ input parameters at the scale $M_{\text {SUSY}}$ which per default is given as in Eq. (126). Consequently, depending on the chosen renormalization scheme for the computation of the higher-order corrections the input parameters have to be converted to the applied scheme where necessary. For example, if we use OS renormalization in the stop sector then the soft SUSY-breaking parameters ($\tilde{m}_{Q_3}^2$, $\tilde{m}_{t_R}^2$, $A_t$) affecting the stop sector must be converted from the SLHA $\overline{\text{ DR }}$ parameters to OS parameters. With these converted parameters the NLO width is calculated then. In Ref. [45] we outlined in detail the procedure applied in NMSSMCALCEW to convert the input parameters. In the following we show the change in the LO and NLO widths for the electroweakino and sfermion decays when applying different renormalization schemes after consistently converting the input parameters. The benchmark point used in the plots is the same as for the investigation of the impact of CP-violation in the previous Sect. 5.7, we only vary $\tan \beta$ in the following. In order to quantify the renormalization scheme dependence we introduce

$$\begin{aligned} \Delta _{ \Gamma }= \left| \frac{\Gamma ^{\mathrm{OS}}-\Gamma ^\mathrm{{\overline{DR}}}}{\Gamma ^{\mathrm{OS}}} \right| , \end{aligned}$$

(143)

where $\Gamma ^{\mathrm{OS}}$ $(\Gamma ^{\mathrm{{\overline{DR}}}})$ denotes partial width evaluated in the OS ($\overline{\mathrm{DR}}$) scheme. It should be noted that in both renormalization schemes we use the loop-corrected masses for the external lines only while we use tree-level masses and tree-level couplings for particles inside loops. For our chosen parameter point, we present the tree-level and loop-corrected masses for the electroweakinos in Table 2, for the stops/sbottoms in Table 3, and for the staus/tau-sneutrino in Table 4.

Table 2 Masses (in GeV) and main components of the neutralino and chargino mass eigenstates at tree level and one-loop level in the two renormalization schemes OS1 and ${{\overline{\mathrm{DR}}}}$

Table 3 The tree-level and one-loop corrected stop and sbottom masses in the ${{\overline{\mathrm{DR}}}}$ and the OS scheme

Table 4 The tree-level and one-loop corrected stau and tau sneutrino masses in the ${{\overline{\mathrm{DR}}}}$ and the OS scheme

Fig. 9

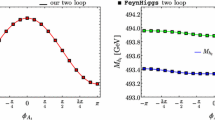
The partial decay width for the decays of $H^+$ into the electroweakino final states ${\tilde{\chi }}_1^+{\tilde{\chi }}_1^0$, ${\tilde{\chi }}_1^+{\tilde{\chi }}_2^0$, ${\tilde{\chi }}_1^+{\tilde{\chi }}_3^0$ as a function of $\tan \beta$ for OS1 (red) and $\overline{\text{ DR }}$ (blue) renormalization at LO (dashed) and NLO (full). Lower insert: the relative difference in the widths due to different renormalization schemes at LO (dashed) and NLO (full)

Figure 9 shows the LO and NLO widths for the charged Higgs decays into the exemplary electroweakino final states ${\tilde{\chi }}_1^+ {\tilde{\chi }}_1^0$, ${\tilde{\chi }}_1^+{\tilde{\chi }}_2^0$, and ${\tilde{\chi }}_1^+ {\tilde{\chi }}_3^0$, respectively, for OS1 renormalization¹⁵ (red) and for $\overline{\text{ DR }}$ renormalization (blue) at LO (dashed) and NLO (full) as a function of $\tan \beta$. The lower insert displays $\Delta \Gamma$ where in the definition Eq. (143) OS has to be replaced by OS1. As we can inferred from the plots for all three decays the dependence on the renormalization scheme decreases when going from LO to NLO, as expected. For the ${\tilde{\chi }}_1^+ {\tilde{\chi }}_1^0$ and ${\tilde{\chi }}_1^+{\tilde{\chi }}_3^0$ final states, already at LO the dependence is very small with $\Delta _\Gamma \approx 1.5$% for the former and 0.32% for the latter, almost independently of $\tan \beta$. It gets reduced to close to 0% at NLO. For the ${\tilde{\chi }}_1^+ {\tilde{\chi }}_2^0$ final state the LO difference between OS1 and $\overline{\text{ DR }}$ renormalization is larger than in the other decays, as is the relative NLO correction to the decay width in the OS1 scheme. For this final state the LO dependence on the renormalization scheme gets reduced from about 18% to 3% at NLO. These results are in accordance with the observed small dependence of the loop-corrected final state masses on the renormalization scheme, cf. Table 2.

Fig. 10

The partial decay width for the decay $H^+ \rightarrow \tilde{t}_1 \tilde{b}_1^*$ as a function of $\tan \beta$ for OS (red) and $\overline{\text{ DR }}$ (blue) renormalization in the stop sector at LO (dashed) and NLO (full) for the SUSY-EW (left) and the SUSY-QCD corrections (right). Lower insert: The relative difference in the widths due to different renormalization schemes at LO (dashed) and NLO (full)

In Fig. 10 we display the LO and the NLO widths for the charged Higgs decay into $\tilde{t}_1 \tilde{b}_1^*$ for OS renormalization (red) and for $\overline{\text{ DR }}$ renormalization in the stop sector (blue) at LO (dashed) and NLO (full) for the SUSY-EW (left) and the SUSY-QCD corrections (right), as a function of $\tan \beta$. The lower insert displays $\Delta \Gamma$ as defined in Eq. (143). As expected, the plots show that the LO dependence on the renormalization scheme gets reduced when going to NLO, both for the SUSY-EW and the SUSY-QCD corrections, namely from about 38% (39%) to 35% (37%) for the SUSY-EW corrections for $\tan \beta =4.5$ (6.5). For the SUSY-QCD corrections the reduction is more important, going down to about 30%. The overall larger dependence on the renormalization schemes compared to the electroweakino final states is also reflected in the larger dependence of the final state squark masses on the renormalization scheme, cf. Table 3.

Figure 11 shows the $H^+ \rightarrow {\tilde{\tau }}^* {\tilde{\nu }}_\tau$ decay (summing over the two possible ${\tilde{\tau }}_i$ ($i=1,2$) states) for OS (red) and the $\overline{\text{ DR }}$ (blue) renormalization at LO (dashed) and SUSY-EW NLO (full) as a function of $\tan \beta$. For the chosen parameter point the SUSY-EW corrections are rather small, and the rather small dependence on the renormalization scheme at LO with $\Delta _\Gamma = 5\%$ gets reduced to 1% at NLO.

Fig. 11

The partial decay width for the decays into stau-sneutrino pairs as a function of $\tan \beta$ for OS (red) and $\overline{\text{ DR }}$ (blue) renormalization at LO (dashed) and NLO (full). Lower insert: The relative difference in the widths due to different renormalization schemes at LO (dashed) and NLO (full)

6 Conclusions

In this paper we complete the computation of the NLO SUSY-EW and SUSY-QCD corrections to the charged Higgs boson decays in the CP-conserving and CP-violating NMSSM that was started in a previous paper with the corrections to the charged $W^+$ plus Higgs boson final states. We provide the missing corrections to the on-shell two-body decays into the SM fermion, the electroweakino and the sfermion final states. For the decays into electroweakinos and sfermions we provide the corrections for different renormalization schemes, chosen to be OS and $\overline{\text{ DR }}$. This allows us to roughly estimate the remaining theoretical uncertainty due to missing higher-order corrections. All corrections have been implemented in the code NMSSMCALCEW thereby combining them with the already incorporated state-of-the-art higher-order QCD corrections.

In our numerical analysis we find that the newly computed SUSY-EW and SUSY-QCD corrections are significant and need to be included for meaningful predictions of the decay branching ratios. In specific corners of the parameter space with small LO widths and/or large mixing effects the corrections can become very large. As for the dependence on the CP-violating phases of the various parameters the effects are of typical size for radiatively induced CP violation. The investigation of the renormalization scheme dependence shows a good perturbative convergence of the higher-order corrections. Our results contribute to the improvement of the precision on the predictions for Higgs boson observables in beyond-the-SM extensions that is required for the correct interpretation of new physics effects being looked for at the LHC.