DNS of Turbulent Premixed Ammonia/Hydrogen Flames: The Impact of Thermo-Diffusive Effects

Abstract

Direct Numerical Simulations (DNS) of three-dimensional premixed turbulent hydrogen-air flames enriched with 19%, 36%, 44% and 57% of NH$_3$ (in volume) are performed. Starting from an equivalence ratio of 0.44 for the case with 19% of NH$_3$, richer mixtures of $\phi =$ 0.54, 0.69 and 0.95 are considered when increasing NH$_3$ concentration to obtain comparable laminar flame speeds, i.e., 0.17 m/s for 19% and 36 % NH$_3$ enriched case, and 0.30 m/s when NH$_3$ concentration is increased to 44 and 57%. The composition and characteristics of the studied mixtures enable to investigate the effects of thermo-diffusivity in a turbulent flow and the role of chemistry and stretch effects in the development of the flames. Given a composition of ammonia and hydrogen and an equivalence ratio, a predictive method is described to identify compositions where thermo-diffusive effects impact the flame and predict the stretch factors. Two maps are proposed to achieve this: the first one is based on the Markstein number and the second one is based on the ratio of consumption speed of strained flames over the laminar unstretched flame speed. This prediction can guide model selection and help manufacturers and experimentalists identify relevant operating points based on desired energy output.

1 Introduction

Recent interest in decarbonizing energy systems such as gas turbines, internal combustion engines, boilers and furnaces is leading to an interest in utilizing carbon-free fuels such as hydrogen (H$_2$) or ammonia (NH$_3$). However, integrating these new fuels into combustors is challenging. For instance, H$_2$ large flame speed at stoichiometry and wide flammability ranges, not only require potential chamber redesign but also raise safety concerns regarding transportation and storage (Staffell et al. 2019). In contrast, NH$_3$ is easier to store and transport (MacFarlane et al. 2020) but its major drawback is its low flame speed which limits its direct use in combustion systems. To offset this, researchers have explored the potential of mixing NH$_3$ with H$_2$ to find a compromise between each fuel’s advantages and drawbacks (Ichikawa et al. 2019; Valera-Medina et al. 2021).

In this context, high fidelity Direct Numerical Simulation (DNS) can be employed in combustion research to investigate the properties of such multi-fuel combustion, supporting the development and validation of combustion models (Rogallo and Moin 1984; Orszag 1970; Domingo and Vervisch 2022). Work on laminar and turbulent premixed combustion of ammonia/hydrogen fuel mixtures has highlighted the importance of thermo-diffusive effects. Indeed, some mixture’s thermo-chemical and transport properties will lead to intrinsic instabilities, which are not caused by external sources. Two major types of instabilities can be distinguished: the hydrodynamic instabilities (Darrieus 1938; Landau 1988) and thermo-diffusive instabilities (Barenblatt 1962). The first cause flame speed modulation due to thermal expansion, and are unconditionally destabilizing at any wavelength. The latter stabilizes or destabilizes the flame compared to the hydrodynamic instabilities. Thermo-diffusively unstable mixtures occur at small scales, with sizes close the flame thickness, and are due to a competition between the deficient reactant’s diffusivity and the temperature diffusion’s speed (Matalon 2007). This can be characterized by the Lewis number: when the deficient reactant is slower than temperature, typically characterized by Lewis number above 1, thermo-diffusive effects are stabilizing. When the deficient reactant is faster than the heat diffusion, which is also called preferential diffusion of light or fast diffusing species, the Lewis number is lower than one and thermo-diffusive effects are destabilizing. Although intrinsic instabilities are understood in the context of laminar flames (Berger et al. 2022; Gaucherand et al. 2023), the investigation of unstable mixtures in turbulent flows is also relevant (Berger et al. 2022). In regards to laminar ammonia and hydrogen mixtures, Wiseman et al. (2021) performed a comparison of numerical and experimental studies of the blowout behavior of a lean ($\phi$ = 0.45) turbulent 3-D premixed NH$_3$/H$_2$/N$_2$ flame, finding preferential diffusion effects, reaching an increase of the flame speed of two times of an unstretched flame in the same conditions. A large increase of the flame surface area and fuel consumption rate was observed, which was related to hydrogen’s preferential diffusion and prevented extinction. DNS of spherically expanding turbulent NH$_3$/H$_2$-air flames with different fuel ratios and equivalence ratios found important distortion due to equivalence ratio local variation, and more wrinkling as H$_2$ content increased (Mukundakumar and Bastiaans 2022). This study was limited to an equivalence ratio between 0.8 and 1.2. In a study with premixed turbulent flames (Yang et al. 2022) at elevated pressure, stronger wrinkling was found at an equivalence ratio of 0.9 for pure NH$_3$ and NH$_3$/H$_2$ mixtures (with up to 15% of H$_2$ in the fuel in volume fraction) compared to the rich ($\phi$ = 1.1) and stoichiometric mixtures. 2-D and 3-D DNS of turbulent ammonia/hydrogen flames at different pressures have also been performed by  Rieth et al. (2022) finding thermo-diffusive effects and local enrichment of positively curved portions of the flame at $\phi$ = 0.45 for a NH$_3$/H$_2$/N$_2$ mixture of respectively 40%/45%/15% in volume fraction in the fuel. Another study by the same authors investigated the formation of NO$_x$ with regards to the observed enrichment in turbulent flames (Rieth et al. 2023). NO$_x$ production was also investigated both in laminar and turbulent ammonia/hydrogen flames with 40% of hydrogen at stoichiometry (Karimkashi et al. 2023), where NO production was lower in positive curvature zones, a phenomenon attributed to H$_2$ preferential diffusion in these zones which was also observed by Netzer et al. in a 2-D laminar study (Netzer et al. 2021) with the same fuel mixture as Rieth et al. but with equivalence ratio from 0.3 to 1.1. Netzer et al. also considered ammonia cracking proportions with 72%/21%/7% of NH$_3$/H$_2$/N$_2$. The behavior of lean, unstable, ammonia/hydrogen premixed mixtures does not seem to differ largely from what is known for pure hydrogen flames. Indeed, in pure hydrogen lean flames ($\phi$ = 0.45 in Coulon et al. (2023) and 0.4 in Berger et al. (2019)), turbulent premixed simulations have identified flame surface reduction and flame consumption speed increased due to thermo-diffusive effects from hydrogen’s preferential diffusion. These results indicate that equivalence ratio and fuel composition affect the development of thermo-diffusive effects. Hydrogen has been investigated both theoretically, numerically and experimentally for a long time (Im and Chen 2002; Lee et al. 2022): preferential diffusion phenomena in hydrogen-premixed flames and specifically lean flames have been discussed in the literature, notably by  Matalon (2007) and Lipatnikov and Chomiak (2005). Hochgreb (2023) highlighted in a recent review, the large flame speed laminar and turbulent flame speeds of hydrogen could reach, notably due to the thermo-diffusively unstable nature of these mixtures, and on the need of combustion models to account for the impact these thermo-diffusive effects in these flames. A large number of work has highlighted the need for lean H$_2$ flames to account for the flame speed increase due to thermo-diffusive effects in combustion model (Berger et al. 2022; Aniello et al. 2022). In the case of NH$_3$/H$_2$ mixtures, the same need has been identified (Gaucherand et al. 2023), but the limited mixture composition investigated in the literature  (Netzer et al. 2021; Wiseman et al. 2021; Mukundakumar and Bastiaans 2022; Yang et al. 2022; Rieth et al. 2022, 2023; Karimkashi et al. 2023; Coulon et al. 2023) still raises the question of the range of conditions where thermo-diffusive effects impact turbulent flames in ammonia/hydrogen blends, and at which intensity.

In order to investigate the effects of unstable ammonia/hydrogen mixtures in turbulent flows, this article presents four DNS of turbulent premixed NH$_3$/H$_2$ flames in a slot burner configuration. The objective of the simulations is twofolds: the first one is to create a database of turbulent premixed NH$_3$/H$_2$ flames, with equivalence ratio varying between 0.44 and 0.95, and NH$_3$ content varying between 19% and 54% in volume. Cases A (19% of NH$_3$, $\phi = 0.44$) and B (36% of NH$_3$, $\phi = 0.54$) have a similar flame speed, and so do Cases C (44% of NH$_3$, $\phi = 0.69$) and D (57% of NH$_3$, $\phi = 0.95$). Indeed, ammonia/hydrogen mixtures are notably investigated to phase out carbon-based fuels such as methane in engines. Methane-based engines operate at various load and equivalence ratios, going from very lean to stoichiometric. Therefore, representative conditions of the laminar flame speed of lean methane flames were picked and two target flame speeds were selected: 0.17 m/s which is representative of a lean methane flame of $\phi \approx 0.7$ and a flame speed of 0.30 m/s which is representative of a lean methane flame of $\phi \approx 0.85$. As the two laminar flame speeds are targeted, the equivalence ratio and ammonia/hydrogen fuel content are tuned using two combinations.

The second objective is to study the proposed flames and gain in understanding on their flame structure and response to thermo-diffusive effects. Furthermore, in terms of modeling, questions remain on the appearance of thermo-diffusive effects in NH$_3$/H$_2$ flames and the construction of models for flame speed enhancement observed in the DNS flames. The numerical setup and DNS solver are presented in Sect. 2. Section 3 shows the flame topology and preferential diffusion impact on the flame structure. A predictive method is developed and tested on the DNS to investigate the mixture’s tendency to have a stretch factor higher than unity based on the mixture composition and one-dimensional flames. This prediction can guide model selection and help manufacturers and experimentalists identify relevant operating points based on desired energy output.

2 Theory, Numerical Setup and Methodology

2.1 Numerical Solver and Chemistry

In this work, the flow is modeled by the reacting Navier–Stokes equations with the compressible solver AVBP¹ (Schönfeld and Rudgyard 1999), an explicit massively parallel code. A third-order accurate in space and time Taylor-Galerkin finite-element scheme is used for the discretization of the convective terms, while a second-order Galerkin scheme is used for diffusion terms (Colin and Rudgyard 2000).

The flow is gaseous and NH$_3$/H$_2$-air chemistry is modeled using an analytically reduced chemistry mechanism which is reduced from CRECK (Stagni et al. 2020) with the in-house software Arcane (Cazères et al. 2021), composing 14 transported species, 7 species with QSS assumption and 88 reactions. Validation of the reduced chemistry is included in the Supplementary Materials. A power law is used to compute the molecular viscosity. Constant Schmidt Sc and Prandtl Pr numbers are used for species molecular diffusion: $D_k = \mu /Sc_k$, for species k, and for thermal conductivity: $\lambda = \mu C_p/Pr$ with $C_p$ the specific heat capacity of the mixture. Pr of 0.7 is selected as it corresponds to the Prandtl number of air, the main component in the premixed mixtures.

2.2 Numerical Set-up and Boundary Conditions

The target configuration corresponds to a turbulent slot burner where burned gases are initiated in the domain and surround fresh gases. Turbulence is injected in the central zone of one-third of the inlet (Fig. 1). The 3-D domains are parallelepiped with dimensions $L_x \times L_y \times L_z$ given in Table 1. The dimensions $L_x$ are chosen based on the estimated flame brush from simulations with a coarser grid (3 points in the flame front). Domains are discretized on regular Cartesian meshes composed of $N_x \times N_y \times N_z$ hexahedral cells of size $\Delta x$ given in Table 1. Laminar 1-D planar unstretched flames were first computed, initialized with Cantera (Goodwin et al. 2022) solutions, to determine the spatial resolution of species mass fractions, temperature and density profiles and to choose an adequate number of points ($N_c$) in each thermal thickness $\delta _L^0$:

$$\begin{aligned} \delta _L^0 = \frac{T_{ad} - T_u}{max(\nabla T)}, \end{aligned}$$

(1)

where $T_u$ is the initial flame temperature (300K), and $T_{ad}$ is the adiabatic flame temperature. The flames are computed at atmospheric pressure. At least 12 points are ensured in the flame front.

Fig. 1

Set-up of the 3-D DNS simulations. Two coflows of burnt gases of each respective cases surround the injection of fresh gases where turbulence is also injected following a Passot-Pouquet spectrum

The injection of turbulence at the inlet corresponds to homogeneous and isotropic turbulence using a Passot-Pouquet turbulence spectrum (Passot and Pouquet 1987) where the turbulent intensity $u'$ corresponds to 10% of the bulk velocity ($U_{bulk}$ = 25 m/s) injected in the central slot. For the details regarding the generation of turbulence through a Fourier series decomposition, readers are referred to Kraichnan (Kraichnan 1970). The spectra decay slowly over time and more details are presented in the Supplementary Materials. A smooth transition from $U_{bulk}$ to $U_{coflow}$ is enforced through a hyperbolic tangent function between the central fresh gas jet and the burnt gas coflow surrounding it. The domain is periodic in the spanwise direction (z), no-slip conditions are specified in the crosswise direction (y) and static pressure is imposed at the outlet. Both inlet and outlet boundary conditions are treated with the Navier–Stokes Characteristic Boundary Conditions (NSCBC) (Poinsot and Lele 1992). More details for the description of the setup, and information on turbulent injection and shear turbulence development, can be found in Coulon et al. (2023) and is reported in the Supplementary Materials. Table 1 presents the parameters of the four 3-D simulations performed, with the NH$_3$ content in volume, equivalence ratio $\phi$, u’/s$_l^0$, l$_t$/$\delta _L^0$, which are needed in order to compute Karlovitz number Ka $=(l_t/\delta _L^0 )^{-{1/2}}(u'/s_L^0)^{3/2}$, Reynolds number $Re = U_{bulk}H / \nu$, where $\nu$ is the kinematic viscosity of the mixture, the turbulent Reynolds number Re$_t = u' l_t/\nu _u$, the laminar flame thickness $\delta _L^0$, cell size $\Delta _x$, numbers of points in thermal thickness $N_c = \delta _L^0 / \Delta _x$, lengths in x, y and z direction $L_x$, $L_y$, $L_z$, and numbers of points in x, y and z direction $N_x$, $N_y$, $N_z$. With H the height of the central jet, corresponding to one-third of L$_y$. $l_t$ is the integral length scale of the turbulence spectrum, corresponding to one-fourth of H (Poinsot and Veynante 2005; Domingo and Vervisch 2022). The four flames are situated in the thin reaction zone defined by the Borghi-Peters diagram (Borghi 1985; Peters 2000) which is presented in the Supplementary Materials. The simulations are performed during two flow-through times.

Table 1 Parameters and mesh information of the simulations with NH$_3$ content in volume, equivalence ratio $\phi$, laminar flame speed s$_l^0$, u’/s$_l^0$, l$_t$/$\delta _L^0$, Karlovitz number Ka, Reynolds number Re, turbulent Reynolds number Re$_t$, laminar flame thickness $\delta _L^0$, cell size $\Delta _x$, numbers of points in thermal thickness $N_c$, lengths in x, y and z direction $L_x$, $L_y$, $L_z$, and numbers of points in x, y and z direction $N_x$, $N_y$, $N_z$

3 Results and Discussion

3.1 Premixed Turbulent NH$_3$/H$_2$-air Flames

Figure 2 displays snapshots of heat release rate normalized by the maximum heat release rate of the 1-D unstretched flame for the four flames after two flow-through times at a cut in the z-axis. Figure 3 presents the contour of local equivalence ratio $\phi$ minus the initial equivalence ratio in the fresh gases.² This normalization is to visualize the effects of preferential diffusion on the flame: the equivalence ratio found in the turbulent flame brush reaches larger (as well as lower) values than the injected equivalence ratio when preferential diffusion becomes significant.

A shorter flame brush length is captured for leaner cases (A, B and C). Zones of high heat release rate are captured along the flame front for all cases. In Case A, for example, the heat release rate in the 3-D DNS is up to five times higher than the maximum heat release rate of the equivalent unstretched laminar case. Strong variations of the equivalence ratio are also seen in all cases. The following sections detail these observations.

Fig. 2

Contour of heat release rate normalized by the maximum heat release rate of the unstretched flames for the four flames after two flow-through times at a cut in the center of the z-axis

Fig. 3

Contour of equivalence ratio minus the initial equivalence ratio in the fresh gases for the four flames after two flow-through times at a cut in the center of the z-axis

3.1.1 Progress Variable Definition

The combustion process of NH$_3$/H$_2$ mixtures needs to be parameterized using an appropriate definition of the progress variable. A modeling strategy to characterize preferential diffusion effects is the use of two controlling variables to parameterize the scatter of the mixture. This has been established for different fuels such as hydrogen (Berger et al. 2022; Böttler et al. 2023), methane (Oijen et al. 2010; Kuenne et al. 2011) or syngas (Zhang et al. 2021) exhibiting preferential diffusion effects. The following two controlling variables are commonly used:

• a progress variable c,

• a mixture fraction Z.

The definition of the mixture fraction is well established, and the Bilger’s expression is used (Bilger et al. 1990). However, an appropriate progress variable definition in the case of ammonia/hydrogen needs to be defined. Furthermore, many modeling strategies rely on tabulation and the thermochemistry of the reacting flow from burn to unburned gas can be mapped in the composition space described by the combination of progress variable and mixture fraction. Two constraints are imposed on the progress variable: a monotonous growth from fresh (c = 0) to burn gas (c = 1) to uniquely describe each thermochemical state and the thermochemical variables should vary at a moderate speed with the progress variable, since, if not verified, it would mean a small deviation in c would result in large errors in the thermochemical variables (Ihme et al. 2012; Niu et al. 2013; Prüfert et al. 2015). Typical definitions for the progress variable are based on enthalpy (E), temperature (T), density ($\rho$), one species or a combination of several species. Recent work involving mixtures of ammonia and hydrogen have proposed H$_2$O (Rieth et al. 2023; Wiseman et al. 2021; Mukundakumar and Bastiaans 2022; Netzer et al. 2021) as the progress variable, a combination of products H$_2$O/NO/NO$_2$ (Chi et al. 2023), or temperature (Karimkashi et al. 2023). Other studies focusing on pure hydrogen have investigated the use of H$_2$ or H$_2$O to describe the scatter of heat release rate obtained for turbulent 3-D DNS (Berger et al. 2022) and for, initially laminar, perturbated 2-D DNS (Berger et al. 2022). The database of the four 3-D DNS NH$_3$/H$_2$-air flames is at first used to select the most suitable progress variable c that would reduce the error in describing the scatter of important parameters Q such as heat release rate $\dot{\omega }_T$ and equivalence ratio $\phi$. Given a quantity Q, an irreducible error $\epsilon _{\textrm{irr}}^2$ can be defined as:

$$\begin{aligned} \epsilon _{\textrm{irr}}^2=\left\langle (Q-\langle Q \mid c\rangle )^2\right\rangle , \end{aligned}$$

(4)

where $\langle \ \rangle$ is an ensemble average and $\langle Q \mid c\rangle$ is the conditional mean of Q with respect to c. To compare the different cases, Eq. (4) is normalized. For the heat release rate, the normalization is done with respect to the maximum heat release of an unstretched flame of the same composition:

$$\begin{aligned} \epsilon ^{norm}_{\dot{\omega }_{T},irr}=\frac{\epsilon _{irr}^2}{\max \left( \dot{\omega }_{T}^{\text{1-D } }\right) ^2}. \end{aligned}$$

(5)

Similarly, for the local equivalence ratio, $\epsilon ^{norm}_{\phi ,irr}$ is normalized with the global equivalence ratio of the fresh gases. The maximum value of the irreducible error is computed, and the smallest value between the different progress variable definitions indicates that the target quantity Q is well characterized by the parameter c (Berger et al. 2022). Different progress variable definitions found in literature (Rieth et al. 2023; Berger et al. 2022; Chi et al. 2023; Oijen et al. 2010; Lehtiniemi et al. 2006; Pierce and Moin 2004; Knop et al. 2011) are tested:

• $c_{H_2} = 1-\frac{Y_{H_2}}{Y_{H_2,u}}$,

• $c_{NH_3} = 1-\frac{Y_{NH_3}}{Y_{NH_3,u}}$,

• $c_{H_2/NH_3} = 1- \left( X_{H_2}\frac{Y_{H_2}}{Y_{H_2,u}} + X_{NH_3}\frac{Y_{NH_3}}{Y_{NH_3,u}} \right)$,

• $c_{H_2O} = \frac{Y_{H_2O}}{Y_{H_2O,b}}$,

• $c_{H_2O/NO} = \frac{Y_{H_2O}-Y_{NO}}{Y_{H_2O,b}-Y_{NO,b}}$,

• $c_T = \frac{T - T_u}{T_{eq}-T_u}$,

• $c_\rho = \frac{\rho - \rho _u}{\rho _{eq}-\rho _u}$,

• $c_E = \frac{E - E_u}{E_{eq}-E_u}$,

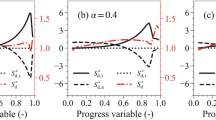
with subscripts b, u, and eq indicating burned, unburned and the equilibrium quantities, respectively. These values were computed using one-dimensional unstretched flames with Cantera. The maximum irreducible errors for $\dot{\omega }_T$ and $\phi$ computed using each definition of c are reported in Fig. 4a and b. In Cases A, B and C, the smallest error for both the heat release rate and the equivalence ratio is found using $\text{c}_{H_2O}$ meaning these target quantities are best parameterized using this progress variable. For Case D, c$_{H_2}$ minimizes the error for the heat release rate but causes the largest error to parameterize the equivalence ratio. The other progress variables give similar error levels for both the heat release rate and local equivalence ratio. Overall, c$_{H_2O}$ appears as a good candidate to be used for describing the two quantities of interest and, therefore, is retained in the rest of this study as the progress variable definition.

Fig. 4

Maximum irreducible error of the heat release rate $\dot{\omega }_{T}$ (top) and the local equivalence ratio $\phi$ (bottom) for different progress variable definitions for the four cases. $\text{c}_{H_2O}$ appears as a good candidate to be used for describing the heat release rate and local equivalence ratio as it reduces the maximum irreducible error for most cases

The large variations of equivalence ratio and heat release rate observed in Figs. 2 and 3 are illustrated in the progress variable space using c$_{H_2O}$ in Fig. 5. The joint probability density functions of these quantities are also reported together with their conditional mean conditioned by the progress variable (black continuous line). The results are compared to the one of 1-D unstretched flame (black dashed line). A very broad distribution is observed for both quantities. In Fig. 5a, Case A exhibits the largest distribution of heat release rate, with values of more than 5 times the maximum heat release computed in the 1-D unstretched case. This diminishes with increasing NH$_3$ concentration (Case A to D) to only two times the maximum one of its unstretched counterpart. Regarding the comparison with the unstretched flame and the conditional mean of the 3-D case, a large deviation is obtained for Case B over the whole range of the progress variable. For Cases A, C and D however, the deviation is largest for progress variable values up to the maximal heat release rate (c$_{H_2O}$ $\approx$ 0.8). At $c>0.8$, the 1-D unstretched case and the conditional mean are superimposed. The deviation from the conditional mean to the 1-D unstretched results of heat release rate are strongest for Case A and declines with increasing equivalence ratio to Case D. Similar results have been found by Wiseman et al. (2021) where a broad distribution of the heat release rate and a deviation of the conditional mean from the unstretched flame was found for a case with 40% NH$_3$, 45% H$_2$, and 15% N$_2$ in the fuel blend and an equivalence ratio of 0.45. The deviation was attributed to large values of strain. Similar results have also been found for lean pure H$_2$ flames (Berger et al. 2022; Coulon et al. 2023; Song et al. 2022; Rieth et al. 2022).

Regarding the equivalence ratio (Fig. 5b), a broad distribution of values is found around the initially imposed equivalence ratio of the fresh gases $\phi _{ref}$. The conditional mean and 1-D results are the same in the fresh and burned gas corresponding to the initial equivalence ratio imposed. In the region in-between, a deviation between the conditional mean and 1-D flame is found: the turbulence affects the inner flame front, causing overall enrichment compared to its 1-D counterpart. The broad distribution of the equivalence ratio indicates preferential diffusion enriching and making the mixture leaner in different places. The probability density function of the equivalence ratio minus the fresh gas equivalence ratio (Fig. 6) informs that all 3D cases have a distribution of equivalence ratio between $\phi _{ref}-0.2$ and $\phi _{ref}+0.1$ and indicates preferential diffusion for the four cases. Compared to the unstretched flames (dashed lines), for which the equivalence ratio is never richer than the global one, the strained 1-D flames (dotted-dashed lines), computed using the twin flame configuration in Cantera, exhibit enrichment. Therefore, these strained elements are responsible for the enrichment in the 3D cases: In Cases A and B, low strain values (10 s$^{-1}$) match the 3-D lean side, and higher strain values (1000 s$^{-1}$) match the 3-D rich side PDF. For Cases C and D, the lean side is matched by low strain values (10 s$^{-1}$ for C and (100 s$^{-1}$ for D). We don’t see a match for the whole range of the PDF on the rich side, but we expect intermediate strain values to match them. The turbulence interacts with the flame and leads to strained flame elements for which the equivalence ratio varies strongly. The impact of the strained elements on the heat release rate of the different cases is investigated later. Finally, the enrichment due to focusing in curved region should not be neglected and also contributes to the overall change in equivalence ratio. A study by (Aspden et al. 2015) tested different transport hypothesis to compare the Lewis number effects (species diffusion vs thermal diffusion) but also the preferential diffusion effects (fuel diffusion vs oxidizer diffusion). In this study, these effects are not separated but are of interest to consider in further study, especially considering the multi-fuel aspect.

Fig. 5

Normalized heat release rate (top) and equivalence ratio (bottom) after two flow-through times with the corresponding joint probability density function of the quantity conditioned by the progress variable c$_{H_2O}$ for the four cases. A lighter shade in the colormap represents a greater probability of the PDF. The dashed line corresponds to the 1-D unstretched laminar flames and the solid line corresponds to the conditional mean of the quantity versus progress variable

Fig. 6

PDF of equivalence ratio minus the reference equivalence ratio over the whole domain for the four cases. Comparison with strained twin flames computed with Cantera (10, 100 and 1000 s$^-1$) and the unstretched flame. Each PDF was normalized by its maximum values to compare the results

3.1.2 Stretch Factor

Another way to estimate the flamelet deviation of lean ammonia/hydrogen mixtures is to compute the stretch factor $I_0$, which accounts for the influence of stretch and measures the deviation between the increase of flame area due to wrinkling and the turbulent flame speed:

$$\begin{aligned} I_0 = \frac{\Omega ^*}{s_L^0}\frac{1}{A_T}, \end{aligned}$$

(6)

with $s_L^0$ the unstretched laminar flame speed and $A_T$, the turbulent flame surface. The total reaction rate $\Omega ^*$ is:

$$\begin{aligned} \Omega ^* = -\frac{1}{\rho _u Y_{f,u}}\int _V \dot{\omega _f} dV, \end{aligned}$$

(7)

is a normalized total volumetric burning rate over the whole volume V. $\rho _u$ is the density of the fresh gases, $Y_{f,u}$, the initial mass fraction of fuel in the mixture, and $\dot{\omega _f}$ is the fuel’s reaction rate. Due to the presence of two fuels in the mixture (H$_2$ and NH$_3$), $\Omega ^*$ is computed using both fuels so that a stretch factor for each fuel $I_{0,NH_3}$ and $I_{0,H_2}$ can be defined. The turbulent flame surface $A_T$ is computed by integrating the flame surface density over the whole flame:

$$\begin{aligned} A_T = \int _V |\nabla c_{H_20} |dV. \end{aligned}$$

(8)

Similar turbulent flame surfaces are obtained for the four different flames, despite shorter flame brush lengths for Cases A, B and C (Figs. 2, 8). This indicates that Cases A, B and C are more wrinkled. Time-averaged values during the second flow-through time of the stretch factors are reported in Table 2.

Table 2 Stretch factor values for the four cases using the reaction rate of NH$_3$ and of H$_2$

Very similar values are found for Cases A, B and C regardless of the fuel considered in Eq. (7). In Case D, the difference between $I_{0,NH_3}$ and $I_{0,H_2}$ is due to the production of H$_2$ by NH$_3$ as will be seen in the following section. As anticipated from Fig. 5, the stretch factor diminishes from Case A to Case D. In Case A values of I$_0$ close to 3 are obtained, indicating that each surface element of the flame front can burn almost 3 times more than the laminar reference flame as a result of the combined effects of turbulence and thermo-diffusive effects. In Case D, I$_0$ is close to unity, which indicates that the increase in the turbulent flame speed is only due to the increase of the flame surface and that combustion in the flame brush proceeds almost as the reference flamelet.

In all Cases, H$_2$ and H notably have very small Lewis numbers and will diffuse faster, leading to preferential diffusion and to the large scatter of equivalence ratio (Fig. 5b). However, since the global initial equivalence ratio (and by extension, the mixture’s global Lewis number) in the fresh gas differs for each case, the impact on heat release rate distribution and stretch factor is different. Case D is close to stoichiometry: the distribution of equivalence ratio due to preferential diffusion is between 0.75 and 1.1. The consumption speed in this range of equivalence ratio in a 1-D unstretched flame reaches a plateau since the local initial equivalence ratio is around stoichiometry. This observation could explain why the conditional mean of heat release rate (Fig. 5a) is closer to the 1-D unstretched flame, and why the stretch factor is close to unity. Figure 7 shows the absolute change of laminar flame speed for the different mixtures of fuel at different equivalence ratios, with $\phi _{ref}$ being the reference equivalence ratio at which the 3-D DNS are initialized. The gradient of flame speed increase is strongest for the leanest case, Case A, and is less steep for Cases B, C and D in that same order. Case D’s flame speed is, as mentioned, reaching a plateau at around $\phi - \phi _{ref} = 0.1$. Hence, despite similar flame speeds of Cases A and B and of Cases C and D, each Cases’ stretch factors are different due to the variation of equivalence ratio and fuel content.

Fig. 7

Absolute change of laminar flame speed for equivalence ratio around the reference equivalence ratio of ± 0.2, which covers the range of equivalence ratio scatter obtained from the 3-D DNS results

Other works have found similar values of stretch factors close to 2 for lean ammonia/hydrogen/nitrogen mixtures with an equivalence ratio of 0.45 (Wiseman et al. 2021). For pure H$_2$, values between 1 and 4 have been found in the literature depending on the equivalence ratio and pressure (Song et al. 2022; Berger et al. 2022; Howarth and Aspden 2022). Our data come as supplemental information to the values of stretch factor ammonia/hydrogen can reach and shows that they can be quite large ($I_0 >2$).

3.1.3 Fuel Flux and Reaction Rate

The fuel flux along the axial direction can be computed as:

$$\begin{aligned} \mathcal {F}=\frac{1}{\rho _{u} U H Y_{f,u}} \int \left\langle \rho u_{x} Y_{f}\right\rangle d y, \end{aligned}$$

(9)

where $\langle \ \rangle$ is the time average during the second flow-through time, U is the bulk velocity, H is the slot size and $u_{x}$ is the axial velocity. Figure 8 shows the fuel consumption $\mathcal {F}$ along the normalized x-axis for the four cases. Case A, B and C consume both fuels ($\hbox {NH}_3$ and $\hbox {H}_2$) faster than Case D: the flame brush is similar for Cases A, B and C, and longer for Case D. Furthermore, for Case D, NH$_3$ is fully consumed by the domain exit, whereas unburned H$_2$ still remains. Indeed, Case D is nearly stoichiometric, and local enrichment from preferential diffusion leads to limited O$_2$ as rich local zones appear, and H$_2$ is produced by NH$_3$. This is further illustrated by the reaction rate of the two species in Fig. 9 where $-\dot{\omega }_f$ is illustrated with f being ammonia and hydrogen. A negative value of $\dot{\omega }_f$ corresponds to fuel consumption, while a positive one corresponds to fuel production. Only Case D is presented here as relevant to the current discussion: between 0.4 $\leqslant$ c $\leqslant$ 0.6, H$_2$ is being produced in non-negligible quantities, due to favorable conditions in terms of fuel proportion and temperature for NH$_3$ to dissociate into H$_2$ (Fig. 9). This production is not obtained for the other cases as presented in the Supplementary Material. These results prove that a surplus of hydrogen due to ammonia decomposing into H$_2$ at moderately high temperatures has a non-negligible effect in Case D explaining why the stretch factor computed with ammonia differs from the one computed with hydrogen (Table 2).

Fig. 8

Fuel consumption of NH$_3$ and H$_2$ for the four cases along the streamwise axis

Fig. 9

Reaction rate in kg/s/m$^3$ of 1-D unstretched flame and conditional mean of 3-D cases for H$_2$ and NH$_3$ for the four cases along the progress variable space

3.1.4 Radical Pool

Chemistry effects influence the stretch factor value: light-diffusing species such as H$_2$ are expected to impact the stretch factor and the resulting heat release rate to be scattered due to preferential diffusion. The impact of intermediate species on preferential diffusion is also worth investigating. Therefore, with the fuel content from the different cases, using 1-D unstretched flame simulations performed using Cantera, the maximum value of the species at different equivalence ratios is computed, as well as the absolute change of the mass fraction, using the equivalence ratio at which the DNSs have been performed as the reference value. The range of equivalence ratios is selected to be somewhat representative of the scatter of equivalence ratio found in the 3-D DNS, where the equivalence ratio is at least around $\pm 0.2$ of the reference value. In the Supplemental Materials, the results for the transported species are presented with the exception of the oxidizer species. Here the focus is on two species with a Lewis number lower than unity, i.e., H and OH. The results are presented in Fig. 10, for the H mass fraction, the mixtures for Cases A, B and C increase around the reference value. The increase of H in Case A for $\phi > \phi _{ref}$ is notably steep. For Case D, the peak of the mass fraction is reached for $\phi - \phi _{ref} = 0.15$, decreasing after this value. The mass fraction of OH increases for the equivalence ratio range for Cases A and B. The evolution of OH for Case C when $\phi > \phi _{ref}$ is slightly less steep than for Cases A and B, but nevertheless increases throughout the range of equivalence ratio investigated. For Case D, the reference equivalence ratio corresponds to where the peak OH production is obtained, meaning a plateau is obtained around this value. The overall increase of light diffusive intermediate species in Cases A, B and C with equivalence ratio contributes to the scatter of heat release rate and equivalence ratio obtained in the 3-D simulations in Figs. 2, 3 and 5. The H radical production and OH production, as local enrichment occurs in the lean Cases A, B and C, illustrate the preferential diffusion effects that affect the 3-D flames. As H and OH increase in the rich, positively curved zones, the consumption speed increases, and the global stretch factor is larger than unity, which indicates that these zones are dominating the flame. On the other hand, the plateau obtained for the production of intermediate species in Case D, either at the reference equivalence ratio, or slightly above is contributing to the attenuated effect of preferential diffusion in 3-D on the scatter of $\phi$ and $\dot{\omega _T}$ and the stretch factor close to unity of Case D.

Fig. 10

Absolute change of the maximum mass fraction of different species of 1-D unstretched flames at varying equivalence ratios using the equivalence ratio at which the 3-D DNS were performed as the reference value

This indicates the mixture’s role in an unstable mixture’s development as the initial equivalence ratio and mixture composition dictate preferential diffusion effects. This further motivates the need for a predictive tool based on the initial equivalence ratio and mixture composition to predict the expected consumption speed and heat release rate increase. However, the flow’s influence on the flame and interaction with the unstable mixture is also noteworthy for investigation and will be looked at in the next section by evaluating the strain and curvature.

3.1.5 Strain and Curvature

The total stretch of the flame K is defined as the sum of the tangential strain rate, $K_s$, and the curvature-induced propagation rate $K_c$ (Poinsot and Veynante 2005):

$$\begin{aligned} K= & {} K_s + K_c, \end{aligned}$$

(10)

$$\begin{aligned} K_c= & {} \kappa s_d, \end{aligned}$$

(11)

$$\begin{aligned} K_s= & {} \nabla \cdot \varvec{u}-\varvec{n}\varvec{n}: \nabla \varvec{u}, \end{aligned}$$

(12)

where $\kappa =\nabla \cdot \textbf{n}$ is the curvature, $\varvec{u}$ is the gas velocity and $\textbf{n} = - \nabla c/|\nabla c|$ is the normal vector to the flame front pointing towards the fresh gases. Positive (negative) curvature elements are convex (concave) towards the burned gases. $s_d$ is the displacement speed, which is the flame front speed relative to the flow (Poinsot and Veynante 2005; Pope 1988) $s_d = (\varvec{w} - \varvec{u} ). \varvec{n}$, or it can also be computed as:

$$\begin{aligned} s_d = \frac{1}{\left| \nabla c\right| }\left( \frac{\partial c}{\partial t}+\varvec{u} \cdot \nabla c\right) . \end{aligned}$$

(13)

The energy equation can also be used to solve $s_d$ on an isocontour of the progress variable. Typically, the value of the progress variable selected is the one where the heat release rate is maximum in the unstretched flame, indicated as $c^*$ and is case dependent. The values of $c^*$ in the study are the following for Cases A, B, C to D respectively: 0.71, 0.76, 0.76, 0.81. $s_d$ is determined with the heat and species diffusive fluxes and the heat release rates on the isosurface of $c^*$ using the following relation (Poinsot and Veynante 2005):

$$\begin{aligned} s_d=\underbrace{\frac{1}{\rho C_p|\nabla T|}\left[ \nabla \cdot \left( \lambda \nabla T\right) +\rho \nabla T \cdot \sum _k\left( \mathcal {D}_k C_{p,k} \nabla Y_k\right) \right] }_{S_{d_{diff}}} + \underbrace{\frac{1}{\rho C_p|\nabla T|}\left( -\sum _k h_k \dot{\omega }_k\right) }_{S_{d_{reac}}}, \end{aligned}$$

(14)

where $\mathcal {D}_k$ is the molecular diffusion coefficient, $C_{p,k}$ is the mass-specific heat capacity, $Y_k$ is the mass fraction, $h_k$ is the enthalpy and $\dot{\omega }_k$ is the mass-production rate for the $k^{th}$ species. Therefore, the displacement speed is a net balance between the reaction rates and diffusive fluxes. The latter can be decomposed into a normal component which is generally oriented in the opposite direction to the normal vector $\textbf{n}$ as defined above, and a tangential component which varies linearly with opposite curvature (Gran et al. 1996; Echekki and Chen 1999). In a steady, unstretched planar laminar flame, the sum of the contribution due to reaction and normal diffusion would be equal to $s_L^0$ (Peters et al. 1998).

The surface average of a target quantity Q can be computed as:

$$\begin{aligned} \langle Q\rangle _{\textrm{S}}=\frac{\left\langle Q \left| \nabla c \right| \mid c^*\right\rangle }{\left\langle \left| \nabla c \right| \mid c^*\right\rangle }, \end{aligned}$$

(15)

where $\langle ... \mid c^* \rangle$ is the conditional average with respect to the isosurface defining the flame front.

The surface averaged mean values of stretch, tangential strain rate and curvature term for the four cases are presented in Fig. 11 using Eq. (14) for $s_d$. Figure 12 shows the probability density function (PDF) of strain and curvature, normalized, respectively, by $\tau$ and $\delta _L^0$ on the same isocontour of progress variable as the surface averaged quantities. The surface averaged curvature-induced propagation rate is negative throughout the flame sheet, whereas the strain-induced rate is positive. This indicates that $\langle K_c \rangle _S$ is responsible for flame surface destruction whereas $\langle K_s \rangle _S$ is responsible for flame surface production in the mean. Positive values of $\langle K_s \rangle _S$ indicate that the flame surface is more stretched than compressed, as confirmed by the PDF of strain in Fig. 12 where the mean value is positive for the four DNS. The tangential strain is piloted by the turbulent flow field as illustrated from the four Cases in Fig. 11, where Cases A and B have a very similar profile of tangential strain surface average and Cases C and D have a similar profile as well, but lower than the one of A and B. Indeed, the laminar flame speed of these cases (A with B, and C with D) are close, and since the same turbulent profile is injected, this indicates that similar turbulence intensity and scales are perceived by A and B, and by C and D. The surface-averaged curvature rate of the four cases does not follow this same trend, where the four cases have a similar profile in $x/H < 3.5$, then after which cases A and C have a similar profile until the end of the flames. The surface-averaged curvature rate of cases B and D is similar until $x/H = 5$ after which they diverge with $\langle K_c \rangle _S$ of Case D being larger. This indicates curvature’s influence by both preferential diffusion phenomena and turbulence. Finally, the surface averaged stretch propagation is controlled for each case, in the first part of the flame, by the tangential strain rate term, and then by the curvature rate term, as the sign of stretch changes from positive to negative. This is due to negative curvature dominating the last end of the flame where the flame is strongly curved and flame bits separate from the flame brush, leading to flame destruction. Similar results have been described for methane (Luca et al. 2019), hydrogen (Coulon et al. 2023; Berger et al. 2022) and hydrogen/ammonia flames (Coulon et al. 2023), and we redirect the reader to these publications for further details on tangential strain and curvature impact on the displacement speed deviation from the unstrained flame speed. In Fig. 13, the density-weighted displacement speed $s_d^* = s_d \rho /\rho _u$ on the iso-surface of progress variable $c^*$ and normalized by the unstretched laminar flame speed of each flame is presented. The positive values indicate that the iso-surface of $c^*$ is moving toward the fresh gases, while the negative values indicate that the iso-surface moves toward the burnt gases. For all cases, the PDF indicates that the iso-surface mainly moves toward the fresh gases. In Fig. 12, the normalized strain PDF of Cases A and B is very close due to their similar laminar flame speed, although the tail of Case A is wider in the positive values especially. Case C and D also have similar PDF of strain profiles, again due to their similar laminar flame speed. The curvature PDF varies with the mean increasing from Case A to D with a wider PDF for Case A.

Fig. 11

Surface average of stretch K and stretch components (tangential strain rate $K_s$, curvature-induced propagation rate $K_c$) along the x-axis of the four DNS cases, normalized by the flame time of each flame ($t_f = \delta _L^0/s_L^0$)

Fig. 12

Probability density function of normalized curvature and tangential strain rate for the four DNS cases

Fig. 13

Probability density function of density-weighted displacement speed normalized by $s_L^0$ for the four DNS cases

As known from literature, positively curved zones will be more enriched than negative ones (Berger et al. 2022; Netzer et al. 2021) in flames with species with Lewis numbers lower than one, leading to the broad equivalence ratio found in Fig. 5b which is due to both the flow structure and the preferential diffusion. However flat flame regions with null curvature also contribute to the deviation from flamelet behavior and lead to higher than unity stretch factor. A recent study (Howarth et al. 2023) has highlighted that flat flame elements are heated after a leading point has passed where preferential diffusion has enhanced the heat release rate and the flame has propagated faster and hotter. The flat flame after the leading point has passed is superadiabatic, which has a higher heat release rate than the unstretched flame. This indicates that both strongly curved elements and flat strained elements contribute to a high heat release rate. To illustrate the effect of strain on heat release, Cantera is used to compute strained flames (twin flame) of the mixtures investigated, where the strained premixed flame is obtained with a counterflow of two streams of fresh gases going against one another, leading to a strained flame (Klimov 1963; Buckmaster and Mikolaitis 1982). The normalized heat release rate of these strained flames is mapped in Fig. 14, where the conditional mean of the 3-D DNS and the unstretched flame speed results are also shown. The strain value of the Cantera flames are 10, 100 and 1000 s$^-1$. Negative strains cannot be computed with one-dimensional strained flame, and, although compressed flame are expected to have an impact on the broad heat release rate scatter, they cannot be investigated here, and the comparison is limited to positive strain rate. For Cases A, B and C, increasing the strain leads to a higher heat release, whereas the opposite occurs for Case D. This is directly linked to the Markstein number of these flames, which is negative for Cases A, B and C and positive for Case D. This indicates the mixture’s sensitivity to strain. Therefore, the scatter of heat release rate in Fig. 5a is due to both the preferential diffusion changing the equivalence ratio and enhanced by curvature effects, and the sensitivity to strain of the mixtures which also affects the heat release rate when preferential diffusion effects are present.

Fig. 14

Heat release rate of 1-D strained twin flames (10, 100 and 1000 s$^-1$) compared with the conditional mean of the 3-D DNS and the unstretched flame

3.2 A Model for Premixed, Turbulent, Thermo-diffusively Unstable NH$_3$/H$_2$ Mixtures

Based on the DNS results, this section aims to develop an a priori model for the modeling of turbulent premixed unstable lean ammonia/hydrogen mixtures. This is done in two steps by computing the stretch factor of any mixtures that are considered unstable by strained flames. The first part of this model, however, is to define the scope in which it should be applied. The predictive assessment method is valid for the range of equivalence ratio and mixture fraction investigated here, at ambient conditions of pressure and temperature, and at the range of turbulence investigated in the previous DNS.

3.2.1 Markstein Length

The first part of the predictive tool uses the Markstein number Ma (or length) theories to identify positive or negative values of the Markstein number and to serve as an indicator of the strain sensitivity to the mixture, as already discussed in Sect. 3.1.5. A map of Markstein number isocontour is computed using the theoretical formula (Bechtold and Matalon 2001; Poinsot and Veynante 2005; Clavin and Joulin 1983):

$$\begin{aligned} Ma = \frac{L_b}{\delta _D} = \frac{\beta \left( L e_{\textrm{eff}}-1\right) }{2(\sigma -1)} \int _1^\sigma \frac{\bar{\lambda }(x)}{x}\ln \frac{ \sigma -1}{x-1} d x, \end{aligned}$$

(16)

where $L_b$ is the Markstein length, $\beta$ is the Zel’dovitch number, $Le_{eff}$ is the effective Lewis number, $\sigma$ is the expansion ratio, $\delta _D = D_{th}/s_L^0$ is the diffusive flame thickness where $D_{th}$ is the thermal diffusivity and $\lambda$ is the thermal conductivity. Defined by Joulin and Mitani (Joulin and Mitani 1981) for two reactant flames, and shown to be generalizable by Sun et al. (1999) for complex reactions, $Le_{eff}$ is given by:

$$\begin{aligned} Le_{eff}=\left\{ \begin{array}{lll} \frac{Le_O+A Le_F}{1+A}, &{} A=1+\beta \left( \phi ^{-1}-1\right) &{} \text{ if } \phi <1, \\ \frac{Le_F+A Le_O}{1+A}, &{} A=1+\beta (\phi -1) &{} \text{ if } \phi >1, \end{array}\right. \end{aligned}$$

(17)

where $Le_F$ and $Le_O$ are the fuel’s and oxidant’s Lewis numbers. In the case of this study, the $Le_F$ is formulated with a mixture-based definition to account for both fuels. The formula used is proposed by Muppala et al. (2009), who suggested a volume-based formulation of the fuel’s Lewis number ($Le_V$), based on the volume fraction ($X_i$) of each fuel in the fuel mixture:

$$\begin{aligned} Le_V = \sum _{n=1}^{f} X_i Le_i, \end{aligned}$$

(18)

with f the number of fuels in the fuel mixture. The Markstein definition and volume-based Lewis number definition were both validated in a previous study (Gaucherand et al. 2023). The Markstein number is computed for a range of NH$_3$/H$_2$ mixture ranging from 0% of NH$_3$ to 60% of NH$_3$. The equivalence ratio ranges from 0.3 to 1.5, depending on the content of NH$_3$ since the equivalence ratio lower bound is higher due to the extinction limit. Figure 15 presents the isocontour of computed Markstein values based on the equivalence ratio and NH$_3$ content in the mixture. The squares correspond to the operating points of the four DNS cases.

Cases A, B and C are, as anticipated, in the negative zone of the Markstein numbers, whereas Case D is very close to 0 but positive. This map provides an evaluation of the sensitivity to strain to different mixtures. The mixtures on the left of the 0 thresholds are expected to be highly sensitive to the thermo-diffusive effects described before and exhibit high values of stretch factors, such as for Cases A, B and C. Mixtures on the right of the threshold are instead expected to have a stretch factor close to unity, as it is for Case D. Of course, this would need to be validated by a larger amount of operating points, but currently, in the literature, the study of turbulent ammonia/hydrogen flames starting at 1 bar and 300K, and the computation of their stretch factor, is scarce.

Fig. 15

Isocontour of Markstein number values based on the ratio of NH$_3$/H$_2$ and equivalence ratio. The 3-D DNS cases are positioned on the map using the squares

If the mixture is stable in the Markstein map, then a unity stretch factor can be considered and no correction to common combustion models is necessary. However, when the mixture is unstable, one should apply a correction for the stretch factor. In the following, we propose a methodology to evaluate the correction with strained flames.

3.2.2 Stretch Factor Derived from Strained Flames

Since the first effect of the Markstein numbers being unstable seems to be the increase of the local laminar flame speed, we show here that this increase is reasonably well captured by simple laminar strained flames. This is further supported by the turbulent flames of the unstable mixtures described in the first part of the discussion section. By modeling the stretch factor effects of complex turbulent flames where thermo-diffusive effects are important with stable 1-D strained flames, one must understand that the 1-D strained flames model is not integrating the entirety of the phenomenon observed in the turbulent flames and discussed before. However, what is suggested here, is that in order to improve modeling of unstable mixtures, a first order approach using the stretch factor from 1-D strained computations would lead to improved results over using I$_0$ = 1. A similar approach as Coulon et al. (2023) is used where the data from a premixed turbulent DNS of lean pure H$_2$ flame was compared to 1-D strained flames at varying equivalence ratio. The comparison differs in the way that, instead of comparing a large range of strain, the simulations are run at iso-strain of $\approx$ 2000 $s^{-1}$ as it is close to the mean value of strain from the DNS data in Fig. 12, and the effects of NH$_3$ content in the fuel and equivalence ratio are investigated. The iso-contour of $s_c/s_L^0$ is considered with $s_c = 1/(\rho _u Y_{f,u})\int _x \dot{\omega _f}dx$ is the consumption speed of the strained flame, and $s_l^0$ the consumption speed of the unstretched flame at the same composition. Strained flames are computed using Cantera using premixed twin flames. We note here that the previous discussion on the flame description included the importance of curvature in turbulent flames and preferential diffusion. However, by accounting for non-unity Lewis in the transport of species, this should have already been taken into account in simulations. Therefore, a model based on the curvature implications should not be necessary. Furthermore, as the separation of the contribution of the stretch component to the flame speed is a complex ordeal, and no simplified setups (such as the twin flame for the strain) exist for the effects of curvature, a model based on the strain and computed with 1-D strained flames seems to be the most straightforward to account for the stretch factor effects and compute the flame speed acceleration.

Fig. 16

Isocontour of the strained derived I$_0^{strained}$ = $s_c/s_L^0$ at 2000s$^-1$ based on the ratio of NH$_3$/H$_2$ and equivalence ratio

Figure 16 presents the results of I$_0^{strained}$ through isocontours of $s_c/s_L^0$. Table 3 compares the results between I$_0^{1D strained}$ and I$_0^{DNS}$ from Table 2. The comparison is done using the stretch factors in the DNS computed with H$_2$, but the results are similar for the NH$_3$ case.

Table 3 Comparison between $I_0^{3D}$ and $I_0^{strained}$ for the four simulations

I$_0^{DNS}$ is well predicted using I$_0^{strained}$ for Cases A, B and C, but not for Case D, validating the use of I$_0^{strained}$ in this a priori model validation of 1-D strained flames as first-order approximations to compute the stretch factor of turbulent unstable mixtures. Regarding Case D, it had a positive Markstein number: the prediction of Fig. 16 using strained flames may only be valid when the Markstein number of a mixture is negative. Of course, integrating a model based on strained flames would require an evaluation the mean flame strain. However, if this is overcome, one can estimate the stretch factor that needs to be accounted for in the ratio of $s_T/s_L^0$ in flamelet modeling using strained flame for parametrization. Although the present results do not evaluate a flamelet modeling approach, it provides insight in the importance of strained laminar flames for turbulent premixed combustion of ammonia/hydrogen, at least in the thin reaction zone. The stretch factor correction suggested is valid for similar conditions of strain as the 3-D DNS, for the range of equivalence ratio, ammonia content, and turbulent conditions from the DNS.

4 Conclusion

Four Direct Numerical Simulations of premixed turbulent flames with detailed chemistry have been performed, for different equivalence ratios and NH$_3$/H$_2$ contents. A progress variable based on H$_2$O is found to be suited to parametrize the combustion of these mixtures as it reduces the irreducible error the most for the scatter of heat release rate and equivalence ratio. The fuel composition and equivalence ratio are found to substantially impact the enhancement of consumption rate, due to preferential diffusion of light-diffusing species leading to local enrichment and generation of thermo-diffusive effects especially so in lean cases as found from the radical pool. Flames with similar flame speeds have similar strain rates and all flames exhibit different curvature, decreasing with equivalence ratio and H$_2$ content. Still, the flame’s stretch factor differs for each flame, going from unity to more than 2, due to thermo-diffusive effects. Based on the mixture composition, an attempt to discriminate which mixtures are expected to be unstable and have a stretch factor higher than unity is done using the Markstein number as an indicator. This is useful for several purposes. From a modeling point of view, it indicates if a model needs to include thermo-diffusive effects or not. A model accounting for preferential diffusion effects in turbulent flames would be relevant for Cases A, B and C, but a standard flamelet model with unity stretch factor would be sufficient for Case D. One-dimensional strained flames are used to see if the stretch factor can be computed a priori for modeling purposes, and the leanest cases are well predicted by the strained flame velocity increase compared to the unstretched one. The development of this tool can serve both for theoretical modeling, to support the choice of model used, and for practical decision-making of operating points for ammonia/hydrogen mixtures for engine manufacturers.