Adaptive Neural Consensus of Unknown Non-Linear Multi-Agent Systems with Communication Noises under Markov Switching Topologies
Abstract
:1. Introduction
2. Problem Description and Preliminaries
2.1. Graph Theory
2.2. Problem Description
2.3. RBFNNs
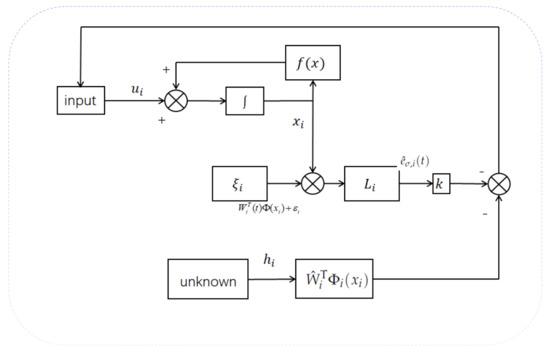
3. Consensus Analysis
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAs | Multi-agent systems |
| RBFNNs | Radial Basis Function Neural Networks |
| NN | Neural Network |
References
- Bae, J.H.; Kim, Y.D. Design of optimal controllers for spacecraft formation flying based on the decentralized approach. Int. J. Aeronaut. Space 2009, 10, 58–66. [Google Scholar] [CrossRef]
- Kankashvar, M.; Bolandi, H.; Mozayani, N. Multi-agent Q-Learning control of spacecraft formation flying reconfiguration trajectories. Adv. Space Res. 2023, 71, 1627–1643. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M.F. Distributed consensus algorithms in sensor networks with imperfect communication: Link failures and channel noise. IEEE Trans. Signal Process. 2008, 57, 355–369. [Google Scholar] [CrossRef]
- Gancheva, V. SOA based multi-agent approach for biological data searching and integration. Int. J. Biol. Biomed. Eng. 2019, 13, 32–37. [Google Scholar]
- Zhang, B.; Hu, W.; Ghias, A.M.Y.M. Multi-agent deep reinforcement learning based distributed control architecture for interconnected multi-energy microgrid energy management and optimization. Energy Convers. Manag. 2023, 277, 116647. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, W.; Liu, W. Multi-agent deep reinforcement learning based distributed optimal generation control of DC microgrids. IEEE Trans. Smart. Grid 2023, 14, 3337–3351. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Contr. 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Contr. 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Contr. 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Cao, Z.; Li, C.; Wang, X. Finite-time consensus of linear multi-agent system via distributed event-triggered strategy. J. Franklin Inst. 2018, 355, 1338–1350. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S. Intentional delay can benefit consensus of second-order multi-agent systems. Automatica 2023, 147, 110750. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Z.; Cui, R. Distributed Optimal Consensus Protocol for High-Order Integrator-Type Multi-Agent Systems. J. Franklin. Inst. 2023, 360, 6862–6879. [Google Scholar] [CrossRef]
- Huang, M.; Manton, J.H. Coordination and consensus of networked agents with noisy measurements: Stochastic algorithms and asymptotic behavior. SIAM J. Control. Optim. 2009, 48, 134–161. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.F. Mean square average-consensus under measurement noises and fixed topologies: Necessary and sufficient conditions. Automatica 2009, 45, 1929–1936. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M. Necessary and sufficient conditions for consensus of double-integrator multi-agent systems with measurement noises. IEEE Trans. Autom. Contr. 2011, 56, 1958–1963. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M. A mean square consensus protocol for linear multi-agent systems with communication noises and fixed topologies. IEEE Trans. Autom. Contr. 2013, 59, 261–267. [Google Scholar] [CrossRef]
- Miao, G.; Xu, S.; Zhang, B. Mean square consensus of second-order multi-agent systems under Markov switching topologies. IMA J. Math. Control. Inf. 2014, 31, 151–164. [Google Scholar] [CrossRef]
- Ming, P.; Liu, J.; Tan, S. Consensus stabilization of stochastic multi-agent system with Markovian switching topologies and stochastic communication noise. J. Franklin Inst. 2015, 352, 3684–3700. [Google Scholar] [CrossRef]
- Li, M.; Deng, F.; Ren, H. Scaled consensus of multi-agent systems with switching topologies and communication noises. Nonlinear Anal. Hybrid. 2020, 36, 100839. [Google Scholar] [CrossRef]
- Guo, H.; Meng, M.; Feng, G. Mean square leader-following consensus of heterogeneous multi-agent systems with Markovian switching topologies and communication delays. Int. J. Robust. Nonlin. 2023, 33, 355–371. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, R.; Zhao, W. Stochastic leader-following consensus of multi-agent systems with measurement noises and communication time-delays. Neurocomputing 2018, 282, 136–145. [Google Scholar] [CrossRef]
- Zong, X.; Li, T.; Zhang, J.F. Consensus conditions of continuous-time multi-agent systems with time-delays and measurement noises. Automatica 2019, 99, 412–419. [Google Scholar] [CrossRef]
- Sun, F.; Shen, Y.; Kurths, J. Mean-square consensus of multi-agent systems with noise and time delay via event-triggered control. J. Franklin Inst. 2020, 357, 5317–5339. [Google Scholar] [CrossRef]
- Xing, M.; Deng, F.; Li, P. Event-triggered tracking control for multi-agent systems with measurement noises. Int. J. Syst. Sci. 2021, 52, 1974–1986. [Google Scholar] [CrossRef]
- Guo, S.; Mo, L.; Yu, Y. Mean-square consensus of heterogeneous multi-agent systems with communication noises. J. Franklin Inst. 2018, 355, 3717–3736. [Google Scholar] [CrossRef]
- Chen, W.; Ren, G.; Yu, Y. Mean-square output consensus of heterogeneous multi-agent systems with communication noises. IET Control Theory Appl. 2021, 15, 2232–2242. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Zhang, A. Stochastic Bipartite Consensus for Second-Order Multi-Agent Systems with Communication Noise and Antagonistic Information. Neurocomputing 2023, 527, 130–142. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Y.; Zuo, Z. Bipartite consensus for multi-agent systems with noises over Markovian switching topologies. Neurocomputing 2021, 419, 295–305. [Google Scholar] [CrossRef]
- Zhou, R.; Li, J. Stochastic consensus of double-integrator leader-following multi-agent systems with measurement noises and time delays. Int. J. Syst. Sci. 2019, 50, 365–378. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Zong, X. Stochastic leader-following consensus of discrete-time nonlinear multi-agent systems with multiplicative noises. J. Franklin Inst. 2022, 359, 7753–7774. [Google Scholar] [CrossRef]
- Zong, X.; Li, T.; Zhang, J.F. Consensus of nonlinear multi-agent systems with multiplicative noises and time-varying delays. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 5415–5420. [Google Scholar]
- Chen, K.; Yan, C.; Ren, Q. Dynamic event-triggered leader-following consensus of nonlinear multi-agent systems with measurement noises. IET Control Theory Appl. 2023, 17, 1367–1380. [Google Scholar] [CrossRef]
- Tariverdi, A.; Talebi, H.A.; Shafiee, M. Fault-tolerant consensus of nonlinear multi-agent systems with directed link failures, communication noise and actuator faults. Int. J. Control 2021, 94, 60–74. [Google Scholar] [CrossRef]
- Huang, Y. Adaptive consensus for uncertain multi-agent systems with stochastic measurement noises. Commun. Nonlinear Sci. 2023, 120, 107156. [Google Scholar] [CrossRef]
- Bao, Y.; Chan, K.J.; Mesbah, A. Learning-based adaptive-scenario-tree model predictive control with improved probabilistic safety using robust Bayesian neural networks. Int. J. Robust Nonlin. 2023, 33, 3312–3333. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, Z.; Cui, B. Impulsive consensus of nonlinear fuzzy multi-agent systems under DoS attack. Nonlinear Anal. Hybr. 2022, 44, 101155. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Wen, G.X.; Liu, Y.J. Adaptive consensus control for a class of nonlinear multiagent time-delay systems using neural networks. IEEE Trans. Neur. Netw. Lear. Syst. 2014, 25, 1217–1226. [Google Scholar] [CrossRef]
- Ma, H.; Wang, Z.; Wang, D. Neural-network-based distributed adaptive robust control for a class of nonlinear multiagent systems with time delays and external noises. IEEE Trans. Syst. Man. Cybern. Syst. 2015, 46, 750–758. [Google Scholar] [CrossRef]
- Meng, W.; Yang, Q.; Sarangapani, J. Distributed control of nonlinear multiagent systems with asymptotic consensus. IEEE Trans. Syst. Man. Cybern. Syst. 2017, 47, 749–757. [Google Scholar] [CrossRef]
- Mo, L.; Yuan, X.; Yu, Y. Neuro-adaptive leaderless consensus of fractional-order multi-agent systems. Neurocomputing 2019, 339, 17–25. [Google Scholar] [CrossRef]
- Wen, G.; Yu, W.; Li, Z. Neuro-adaptive consensus tracking of multiagent systems with a high-dimensional leader. IEEE Trans. Cybern. 2016, 47, 1730–1742. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, C.; Cai, X. Adaptive neural network finite-time tracking control for a class of high-order nonlinear multi-agent systems with powers of positive odd rational numbers and prescribed performance. Neurocomputing 2021, 419, 157–167. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Stone, M.H. The generalized Weierstrass approximation theorem. Math. Mag. 1948, 21, 237–254. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neur. Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, L.; Feng, G. Adaptive optimal control of networked nonlinear systems with stochastic sensor and actuator dropouts based on reinforcement learning. IEEE Trans. Neur. Netw. Lear. 2022, 22, 1–14. [Google Scholar] [CrossRef]
- Wang, D.; Ma, H.; Liu, D. Distributed control algorithm for bipartite consensus of the nonlinear time-delayed multi-agent systems with neural networks. Neurocomputing 2016, 174, 928–936. [Google Scholar] [CrossRef]
- Bao, Y.; Velni, J.M.; Shahbakhti, M. Epistemic uncertainty quantification in state-space LPV model identification using Bayesian neural networks. IEEE Control Syst. Lett. 2020, 5, 719–724. [Google Scholar] [CrossRef]
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Xie, L. Adaptive Neural Consensus of Unknown Non-Linear Multi-Agent Systems with Communication Noises under Markov Switching Topologies. Mathematics 2024, 12, 133. https://doi.org/10.3390/math12010133
Guo S, Xie L. Adaptive Neural Consensus of Unknown Non-Linear Multi-Agent Systems with Communication Noises under Markov Switching Topologies. Mathematics. 2024; 12(1):133. https://doi.org/10.3390/math12010133
Chicago/Turabian StyleGuo, Shaoyan, and Longhan Xie. 2024. "Adaptive Neural Consensus of Unknown Non-Linear Multi-Agent Systems with Communication Noises under Markov Switching Topologies" Mathematics 12, no. 1: 133. https://doi.org/10.3390/math12010133