Produit scalaire
- par gabriel
- dans Mathématiques, Vecteurs
- sur 9 novembre 2019

Rappel et précisions

Un vecteur est caractérisé par :
une direction
un sens sur cette direction
une longueur.
On le nomme soit d’après ses extrémités
![]()
Soit avec une lettre ![]()
La longueur du vecteur est aussi appelée norme et se note 
ou parfois plus simplement ![]()

ou
![]() .
.
Un produit est une multiplication.
Un scalaire est un nombre.
Dans un produit scalaire ont multiplie d’une façon particulière deux vecteurs.
Cette multiplication est notée par un point séparant les deux vecteurs multipliés.
Le résultat de cette multiplication ou produit n’est pas un vecteur mais un nombre, un scalaire, d’où son nom.
Définition 1

Soit ![]() et
et ![]() deux vecteurs que l’on peut nommer aussi respectivement
deux vecteurs que l’on peut nommer aussi respectivement ![]() et
et ![]() .
.
Le produit scalaire noté ![]() ou
ou ![]() est le produit de la norme du premier vecteur par la projection orthogonale du second vecteur sur le premier.
est le produit de la norme du premier vecteur par la projection orthogonale du second vecteur sur le premier.
La projection orthogonale du vecteur ![]() sur le vecteur
sur le vecteur ![]() est
est ![]() .
.![]() est le produit scalaire.
est le produit scalaire. ![]() et
et ![]() sont des vecteurs. Le résultat est le produit de deux longueurs ( deux nombres, deux scalaires).
sont des vecteurs. Le résultat est le produit de deux longueurs ( deux nombres, deux scalaires).![]() est la longueur ou norme du vecteur
est la longueur ou norme du vecteur ![]() et
et ![]() est la longueur de la projection du vecteur
est la longueur de la projection du vecteur ![]() sur le vecteur
sur le vecteur ![]()


Ici on a projeté le vecteur ![]() sur le vecteur
sur le vecteur ![]() .
.
Les vecteurs sont inversés, mais le produit scalaire sera le même.

Soit un triangle équilatéral ABC de 8 cm de côté. Soit I le milieu du côté AB .
Calculons le produit scalaire ![]() .
.
Quelle est la projection orthogonale de AC sur AB ?
La projection orthogonale de A sur AB est évidemment le point A lui même
La projection orthogonale de C sur AB est I. En effet CI est une hauteur de ABC ( CI perpendiculaire à AB). Dans un triangle équilatéral, la hauteur est aussi médiane, médiatrice, …..
Donc la projection orthogonale de AC sur AB est AI.
Nous en déduisons le produit scalaire: voir ci contre.
Définition 2


Reprenons la première figure.
ACH est un triangle rectangle puisuqe AH est la projecton ortogonale de AC sur AB.
Dans ce triangle rectangle nous savons que :
Nous en déduisons que :
Dans la première formule :
On remplace AH par sa valeur :![]()
Qu’on doit écrire avec les normes : voir les formules ci-contre donnant les diverses manières d’écrire cette formule du produit scalaire.
Définition 3


Rappelons que, puisqu’un vecteur est colinéaire à lui même, les deux écritures suivantes sont équivalentes :![]()
![]() .
.
En partant de la première identité remarquable appliquée aux vecteurs et que nous démontrerons plus loin, nous pouvons écrire : 
en isolant le produit scalaire dans le second membre et en écrivant l’équation produite dans l’autre sens :
Il ne reste plus qu’à diviser par 2 les deux membres et remplacer la somme des deux vecteurs : 
On pourrait bien sûr faire une démonstration identique avec les vecteurs AB et AC.
Si on choisit de faire la démonstration avec la deuxième identité remarquable , (a-b)², on obtiendra une autre formule qui est tout aussi valable mais qui donne la différence des deux vecteurs plutôt que leur somme. ![]()
Définition 4, analytique


![]()
Le repère ![]() est un repère orthonormé, ses axes étant orthogonaux et les normes des vecteurs unitaires
est un repère orthonormé, ses axes étant orthogonaux et les normes des vecteurs unitaires ![]() sont égales :
sont égales : ![]() .
.
les 4 points A,B,C, D ont les coordonnées A(Xa;Ya), B(Xb;Yb), C(Xc;Yc) et D(Xd,Yd).
On joint les points A et B puis C et D pour obtenir les vecteurs ![]() ou
ou ![]() et
et ![]() ou
ou ![]() .
.
On calcule les composantes (coordonnées) de chacun de ces vecteurs. 

Les composantes du vecteur ![]() sont x et y.
sont x et y.
Les composantes du vecteur ![]() sont x’ et y’.
sont x’ et y’.
Nous savons qu’un vecteur est égal à x fois le vecteur unitaire des abscisse plus y fois le vecteur unitaire des ordonnées. 
A partir de cette écriture vectorielle, calculons le produit scalaire, puis développons : 
Or :
le produit scalaire de deux vecteurs orthogonaux (perpendiculaires) est égal à 0 (voir plus bas).![]() .
.
Nous en déduisons :
En résumé
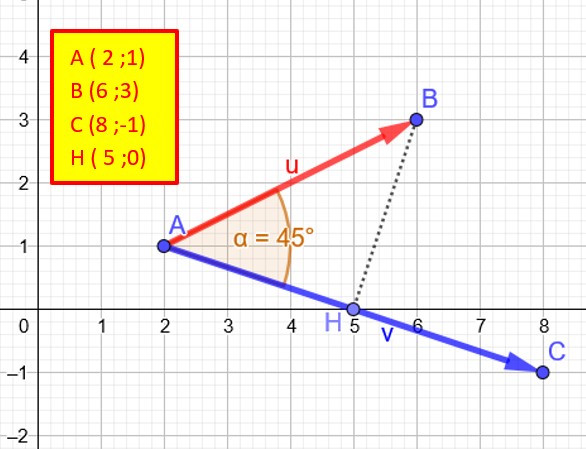




A partir des coordonnées des points A,B,C,D données sur le graphique ci contre, on pet calculer les composantes (coordonnées) des vecteurs ainsi que leur norme (longueur).

Nous allons calculer, à partir de ces données, le produit scalaire des vecteurs AB et AC. en utilisant les 4 définitions.
Le produit scalaire de deux vecteurs est égal au produit de la norme d’un des vecteurs par la projection orthogonale de l’autre vecteur sur lui-même.
Le produit scalaire de deux vecteurs est égal au produit des deux normes de chacun des vecteurs par le cosinus de l’angle formé par les deux vecteurs.
Le produit scalaire de deux vecteurs est égal à la moitié du carré de la norme de leur somme diminué du carré de la norme de l’un et diminué du carré de la norme de l’autre.
Le produit scalaire de deux vecteurs est égal à la somme des produits des composantes horizontales et des produits des composantes verticales des deux vecteurs.
Propriétés
Produit scalaire d’un vecteur avec lui-même :![]()

Produit scalaire de deux vecteurs dont l’un est le vecteur nul :![]()

Le produit scalaire est commutatif :![]()

Le produit scalaire est distributif par rapport à la somme vectorielle :
![]()
il nous faut démontrer cette égalité.![]()
Nous allons utiliser la forme analytique du produit scalaire. Les composantes ou coordonnées des trois vecteurs sont :
Nous écrivons le premier membre de notre formule sous cette forme et nous la transformons en distribuant chaque composante :

On distribue dans le second membre :
On rétablit l’écriture vectorielle :![]()
Le produit scalaire est distributif par rapport à la multiplication par un scalaire.![]()
En utilisant comme pour la propriété précédente la forme analytique, la démonstration est facile et nous vous proposons de la faire.
Si deux vecteurs sont colinéaires et de même sens leur produit scalaire est égal au produit de leur norme. ![]()
SI deux vecteurs sont colinéaires, et de sens contraire, leur produit scalaire est égal à l’opposé du produit de leur norme.
En utilisant la formule :![]()
Si les deux vecteurs sont colinéaires et de même sens leur angle est égal à 0° et cos0°=1.![]()
Si les vecteurs sont colinéaires et de sens contraire, leur angle est égal à 180° et leur cos180°=-1![]()
Si deux vecteurs sont perpendiculaires, leur produit scalaire est nul.![]()
Si deux vecteurs sont perpendiculaires, leurs angle est égal à 90° et cos90°=0![]()
![]()
Applications
Somme de deux vecteurs
Avec le produit scalaire, on peut calculer la somme de deux vecteurs. En particulier, en physique, on peut calculer la résultante de deux forces.

Il s’agit de calculer la résultante des deux forces F1 et F2.
Nous cherchons, parmi les formules du produit scalaire celle dans laquelle on trouve la somme de deux vecteurs. ![]()
Que l’on peut exprimer en écriture simplifiée employée en physique :![]()
Comme on connaît l’angle des deux forces, on peut exprimer le produit scalaire avec la formule correspondant : ![]()
Ou en écriture simplifiée :![]()
Il est évident que ces deux expressions du produit scalaire sont égales, et on peut écrire :
Le reste n’est que calcul :
Travail d’une force.
En physique, le produit scalaire exprime le travail d’une force.
Le travail d’une force est égal au produit scalaire du vecteur force et du vecteur déplacement. 

Autrefois, les péniches qui circulaient sur une rivière ou un canal, étaient tirées par un cheval qui se déplaçait sur un chemin longeant le cours d’eau, appelé chemin de halage.
La force du cheval avait tendance à attirer la péniche vers la berge, mais le gouvernail rectifiait le parcours qui était parallèle aux berges. Cette situation est résumée dans le dessin ci-contre.
La force avec laquelle le chaval tire la péniche est représentée par un vecteur rouge. Sont intensité vaut 600 Newtons.
Le déplacement est représenté par un vecteur violet. Il est égal
à 500 m.
L’angle entre le vecteur force et le vecteur déplacement vaut 30°.
Quel est le travail fourni gratuitement par ce pauvre cheval ? 
Les besoins vitaux d’un cheval sont environ de 9196 kj.Il faudra lui apporter en plus l’équivalent en avoine de 260 kj pour qu’il puisse effectuer ces 500 m en tirant la péniche.
Théorème d’Al Kashi
Il est possible de généraliser le théorème de Pythagore pour les triangles quelconques.
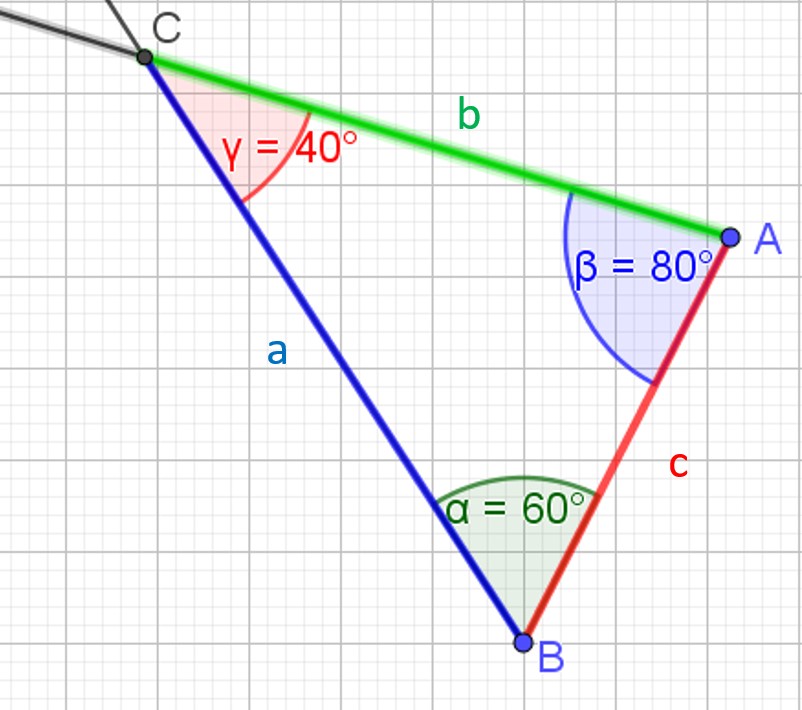

Dans le triangle ABC,
on désigne par a le côté opposé au sommet A,
on désigne par b le côté opposé au sommet B,
on désigne par c le côté opposé au sommet C.
On désigne par α,β et γ les angles respectifs en A,B et C.
D’après la relation de Chasles ou d’après l’addition des vecteurs, on peut écrire :![]()
ou encore ![]()
On élève au carré les deux membres :![]()
On développe le second membre :![]()
le deuxième terme est un produit scalaire qui donne d’après sa deuxième définition :
Soit en écriture simplifiée :
Ou en changeant l’ordre des termes (commutativité de l’addition et de la multiplication) :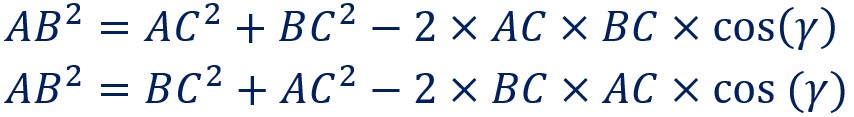
Et enfin en utilisant la notation décrite au début du paragraphe :![]()
Par permutation circulaire on obtient les autres formules décrites ci contre avec la particularité du triangle rectangle.